サイコロを2つまたは3つ以上振る確率の問題は考え方がいくつかあります。
2つの場合は表をつくることですべて解決しますし、3つの場合も表があれば数えることで解決します。
しかし、ここでは重複試行の確率の確認を含めいろいろなパターンの問題を取り上げておきます。
2つのサイコロを振る問題の解き方
これは中学生の確率問題と同じで表を書けば良いだけです。
2つのサイコロを同時に投げたとき、目の和が8となる確率を求めよ。
そのまま中学生の問題です。
2つのサイコロを A、B とすると、これらの目の出方は
\( N=6\times 6=36\)
通りあり、これは同様に確からしい。
このうち目の和が8になるのは
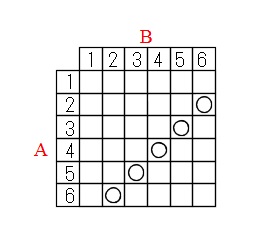
\( (A,B)=(2,6),(3,5)(4,4)(5,3)(6,2)\)
の場合で5通りあります。
よって求める確率は
\( p=\displaystyle \frac{5}{36}\)
表で答が出ます。
3つのサイコロを振る問題の考え方
「1つのサイコロを3回投げる」ことと「3個のサイコロを同時に投げる」というのは同じことです。
「2つの玉を同時に取り出す取りだし方」と考え方は同じです。
表だけで解決する単純な問題
1つのサイコロを3回投げたとき、出た目の和が10となる確率を求めよ。
サイコロ3回の目の出方は全部で
\( N=6\times6 \times 6=216\)
通りあり、これらはすべて等しい確率で起こります。
このうち3回の目の和が10になるのは、
1回目と2回目の目の出方で考えることができます。
例えば、
1回目、2回目のサイコロをA,Bとして
\( (\mathrm{A,B})=(1,3)\)
とすると3回目が6であれば和が10になります。
和が10に限定されているので1回目、2回目に対し3回目は1つだけ対応します。
ところでA,Bの組みに対し和が10になる組とならない組みがあります。
\( (\mathrm{A,B})=(1,1)\)
の場合、3回目は何であろうと和が10にはなれません。
このように和が10にならない組みもあります。
ここではならない(なれない)組を探した方がはやそうです。
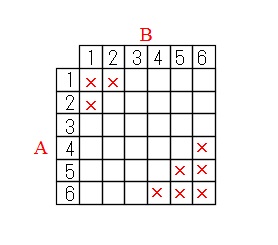
和が10にならない組は36組中9組あります。
逆に10になるのは
\( r=36-9=27\)
となるので
求める確率は
\( p=\displaystyle \frac{27}{216}=\displaystyle \frac{1}{8}\)
ここまでは表で終わらせることができる問題の解き方です。
考え方がカギとなる問題
3個のさいころを投げたとき、出た目の最大値が4以下である確率を求めよ。
また、出た目の最大値が4である確率を求めよ。
「最大値が4以下」と「最大値が4」は違いますからね。
この手の問題はよく出ますが、後半の「最大値が4」って?と思った人が多いでしょう。
まずは前半です。
大 中 小 と3個のサイコロを投げたとき、
目の出方は全部で
\( N=6^3=216\)
通りあります。
「大は4以下の4通り」,「中も4以下の4通り」,「小も4以下の4通り」
であれば何でも良いということなので、
\( r=4\times4 \times 4=64\)
通りあることになり、求める確率は
\( p=\displaystyle \frac{r}{N}=\displaystyle \frac{4\cdot 4\cdot 4}{6\cdot 6\cdot 6}=\displaystyle \frac{8}{27}\)
これは容易です。
次の「最大値が4」とはどういうことかというと、
「大中小 のどれか1つは4であり、5以上の目は無い。」
ということです。
例えば、「大中小」が「333」でもダメ、「335」でもダメ、「241」なら○。
そこで、大を4とする、中を4とする、小を4とする、
と場合を分けることも出来るのですが、
「最大値が4以下であり、すべてが3以下でなければいい」、
と考えれば、
「すべてが4以下」であるのは
\( r_4=4\times4 \times 4=64\)
「すべてが3以下」であるのは、
\( r_3=3\times3 \times 3=27\)
通りであることから、
「最大値に4を持つ」のは
\( r_4-r_3=64-27=37\)
通りあることになります。
よって求める確率は
\( p=\displaystyle \frac{r_4-r_3}{N}=\displaystyle \frac{37}{216}\)
と出せるのです。
ちょっと難しめの考え方なので、図で示してみると、
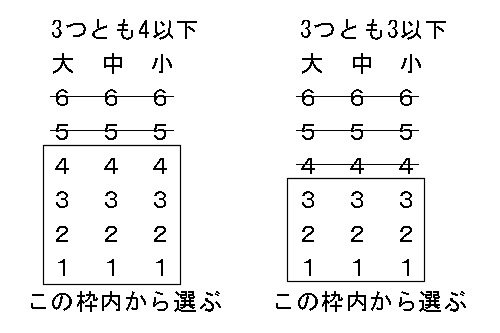
「3つとも4以下」と「3つとも3以下」
この差を取ると、大中小のどれかは4を1つは含んでいることになります。
書き出して見るとすぐ分かりますが、
樹形図の \(4\times 4\times 4\) 通りから \(3\times 3\times 3\) 通りを引けば、
どこかに4を含む樹形図となりますので確認してみると良いです。
この問題はサイコロが何個でも同じです。
\(\,n\,\)個のサイコロを同時に投げるとき、
「出る目の最大値が5である」確率を求めよ。
\(\,n\,\)個のサイコロの目の出方は全部で
\( N=6^n\)
通りあって、これらは等しい確率で起こります。
このうち「出る目の最大値が5である」目の出方は、
「出る目のすべてが5以下である」
中から
「出る目のすべてが4以下である」
出方を除いて、
\( r=5^n-4^n\)
通りあるので求める確率は
\( p=\displaystyle \frac{r}{N}=\displaystyle \frac{5^n-4^n}{6^n}\)
この考え方はポイントになりますよ。
重複試行の確率
さて、これまで確率の基本定理にしたがって確率を求めて来ましたが、少し楽しましょう。
すでに知っているならどんどん使っていいですし、ここで理解してからでもいいので確率を求めるときに楽な計算を選びましょう。
ただ、誘導がある場合は誘導にしたがって計算を進めないと答が出ませんよ。
重複試行の定義
今までは確率を求めるとき、
\( p=\displaystyle \frac{r}{N}\)
のように「条件にあう出方」を「すべての出方」で割るという計算をしていましたが必要無くなります。
同じ試行を繰り返し行うことを、まとめて1つの試行とみなし、
もとの試行の重複試行という。
サイコロを何回も投げる試行のことです。
定義自体はこの際忘れてもかまいませんが、次の定理が重要です。
重複試行の定理
先ずは分かりにくい一般的な式で表しますが、
実際使うときはそれほど使いにくいわけではありません。
1回の試行で事象\(\,A\,\)の起こる確率が\(\,p\,\)であるとする。
このとき、\(n\) 回の重複試行において \(\,A\,\) がちょうど \(\,r\,\) 回起こる確率は
\( _n\mathrm{C}_r\cdot p^r\cdot (1-p)^{n-r}\)
である。
ここに、\(\,n\,\)は自然数、\(\,r\,\)は \(\,0≦\,r\,≦\,n\) を満たす整数である。
この定理に出てくる確率
\( 1-p\)
は A が起こらない、つまり A の余事象の確率です。
\( _n\mathrm{C}_r\)
は \(\,n\,\) 回の試行のうち、A が起こる \(\,r\,\) 回がどこ(何回目)で起こるかを表しています。
独立試行の乗法定理
この定理の前に「独立試行の乗法定理」を復習しておいて下さい。
【独立試行の乗法定理】
2つの独立な試行を行ったとき、
「事象 A と B が起こる」事象の確率は
\( P(A)\times P(B)\) である。
これは試行回数は何回でも関係ありません。
例えば、サイコロを3回振るとき、
「1回目奇数」「2回目偶数」「3回目奇数」
となる確率は、
\( p=\displaystyle \frac{1}{2}\times \displaystyle \frac{1}{2}\times \displaystyle \frac{1}{2}=\displaystyle \frac{1}{8}\)
と求めることができるということです。
おそらく普通につかっていると思いますので気にせず先に進みましょう。
基本問題を解いて終わりにします。
1つのサイコロを6回投げるとき、次の確率を求めよ。
(1)2回目と4回目の2回だけ1の目が出る。
(2)1の目がちょうど2回出る。
(3)1の目が2回以上出る。
サイコロを1回投げるとき
1の目が「出る(○)確率」は \(\displaystyle \frac{1}{6}\) ,
「出ない(×)確率」は \(\displaystyle \frac{5}{6}\) です。
(1)
6回のサイコロの出方は
×-○-×-○-×-×
だけなので順番はそのままで、求める確率は
\( p_1=\displaystyle \frac{5}{6}\times \displaystyle \frac{1}{6}\times \displaystyle \frac{5}{6}\times \displaystyle \frac{1}{6}\times \displaystyle \frac{5}{6}\times \displaystyle \frac{5}{6}\\ \\
=\displaystyle \frac{625}{46656} \)
重複定理の置き場所が固定された、1通りだけをかけていることと同じです。
(2)
今度は置き場所が固定されていません。
○-○-×-×-×-×
○-×-○-×-×-×
○-×-×-○-×-×
….
×-○-×-○-×-×
….
6回中どこで1が2回出るか、を数えなくてはなりません。
\( _6\mathrm{C}_2=\displaystyle \frac{6\cdot 5}{2\cdot 1}=15\)
通りあります。
この1つひとつの確率は
「1が2回、1以外が4回」で \(\displaystyle \left( \frac{1}{6} \right)^2\left( \frac{5}{6} \right)^4\) と、どれも同じです。
よって求める確率は
\( p_2=_6\mathrm{C}_2\times \left( \displaystyle \frac{1}{6} \right)^2\left( \displaystyle \frac{5}{6} \right)^4\\ \\
=\displaystyle \frac{3125}{15552}\)
(3)
これは見た目たいへんそうですよ。
「2回以上」とは「2回」「3回」「4回」「5回」「6回」の場合があります。
(1)(2)を見ても分かるように数字が大きいのでできるだけ計算は少なくしたいです。
そこで余事象ですね。
「1の目が2回以上出る」の余事象は、
「1の目が出る回数が0回か1回」です。
明らかに余事象の方が楽でしょう。
0回出るときの確率は \(\displaystyle \left(\frac{5}{6}\right)^6\)
1回出るときの確率は \(\displaystyle _6\mathrm{C}_1 \left(\frac{1}{6}\right) \left(\frac{5}{6}\right)^5\)
これらから余事象の確率は
\( q =\left(\displaystyle \frac{5}{6}\right)^6+_6\mathrm{C}_1 \left(\displaystyle \frac{1}{6}\right) \left(\displaystyle \frac{5}{6}\right)^5\\ \\
=\left(\displaystyle \frac{5}{6}\right)^6+6\times \left(\displaystyle \frac{1}{6}\right) \left(\displaystyle \frac{5}{6}\right)^5\\ \\
=\left(\displaystyle \frac{5}{6}\right)^6+\left(\displaystyle \frac{5}{6}\right)^5\\ \\
=\left(\displaystyle \frac{5}{6}\right)^5 \cdot \left(\displaystyle \frac{5}{6}+1\right)\\ \\
=\left(\displaystyle \frac{5}{6}\right)^5 \cdot \left(\displaystyle \frac{11}{6}\right)\\ \\
=\displaystyle \frac{34375}{46656}\)
よって求める確率は
\( p_3=1-q\\ \\
=1-\displaystyle \frac{34375}{46656}\\ \\
=\displaystyle \frac{12281}{46656}\)
サイコロを投げる回数を減らしておけば良かったですね。
しかし、余事象に考えがいくように大きいままにしておきます。
求めたい確率は1から余事象の確率\(\,\color{red}{q}\,\)を引けば良いんですよ。
\( p=1-\color{red}{q}\)
ここまで来れば少しは確率も何とか対応できるでしょう。
後は
苦手な分野から対策していきましょう。
