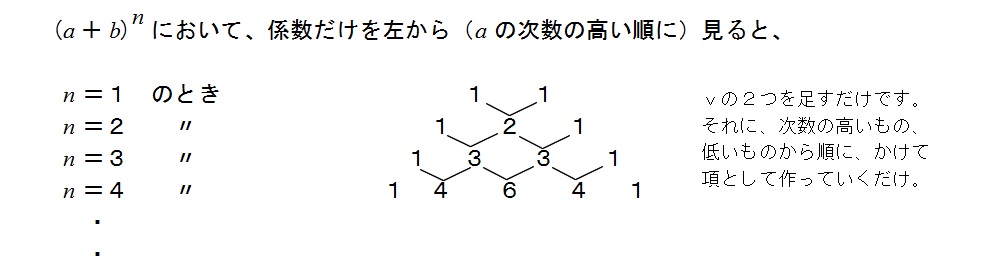
現行では数学Ⅱになるパスカルの三角形と展開公式の係数の関係をお伝えしおきます。
2次の展開公式は中学生の頃に覚えているくらい簡単なものしかありませんでしたが、
3次になると覚えていない高校生もいるのでここで確認しておいてください。
公式の暗記でも良いですが、もし忘れたとしてもパスカルの三角形を思い出せれば問題ありません。
受験で数学Ⅰは必須
数学Ⅰがすべての単元に通じる基本であることはある程度先に進めば誰もが感じることです。
感じなくても良いです。
それが普通ですから。
しかし、いろいろなところで数学Ⅰの知識は使っています。
こちらでも書いていますので確認しておいて下さい。
今回は(4)以降の係数をパスカルの三角形で表した方法です。
(現行ではパスカルの三角形は数学\(Ⅱ\)になっていますが、数学Ⅰでやっておいて良い項目です。
公式は覚えて使うことが先でいいです。
公式は証明なしで使うのはだめだという人もいますがよく考えてみて下さい。
円や球に関する公式を証明出来る人いますか?
少ないでしょう。
でも使います。
証明できなくても、使うことが先で良いんです。
少なくとも数学が苦手だという人は覚えて、使うで良いんです。
次の式を展開せよ。
\( (1) (4x-5y)^2\\
(2) (-2x+5)(-2x-5)\\
(3) (5a+3b)^2\\
(4) (x-3)^3\\
(5) (2a+3b)^3\\
(6) (x-3)(x^2+3x+9)\)
問題をノートに書き写してやって見てください。
パスカルの三角形
(4)はパスカルの三角形を覚えておけば、覚えなくてもいい公式を使います。
しかし、いちいちパスカルの三角形を書かなくても(そんなに時間はかかりませんが)、
この公式は高校最初の公式になるので覚えているでしょう。
\(\color{red}{ (a+b)^3=a^3+3a^2b+3ab^2+b^3}\)
\(\color{red}{ (a-b)^3=a^3-3a^2b+3ab^2-b^3}\)
です。
この項を左から見て下さい。
\( a について見ると\\
a^3\,,\,a^2\,,\,a^1\,,\,a^0(a^0=1)\)
と次数が下がり、
\( b についてみると\\
b^0\,,\,b^1\,,\,b^2\,,\,b^3\)
と次数が上がっています。
\( {(a+b)^n}\)
において係数を考えず係数抜きに文字の次数だけを左から見ると
\( {a^n\,,\,a^{n-1}b^1\,,\,a^{n-2}b^2\,,\,a^{n-3}b^3,\cdots,\,a^1b^{n-1}\,,\,b^n}\)
と並びます。
ここで、
\(\color{red}{ a と b の次数を合わせると n 次になる}\)
ということは見逃さないで下さい。
そして、係数を決めるのがパスカルの三角形です。
「組み合わせ」の計算方法、
\( {_n \mathrm{C} _k}\)
を学んだ後は、「2項定理」として、覚えることになりますが、
このパスカルの三角形が具体的な数値になります。
だから、これを利用すると覚える必要は無いのですが、
\( (a\,+\,b)^4=a^4\,+\,4a^3b\,+\,6a^2b^2\,+\,4ab^3\,+\,b^4\)
なんてのもすぐわかりますよね。
\(\color{red}{ a の次数は下がり、b の次数は上がっている}\)
ことに注意してください。
符号違いの公式の覚え方、使い方
加えて言っておくと、
\( {(a-b)^3=a^3-3a^2b+3ab^2-b^3}\)
は
\( {(a+b)^3=a^3+3a^2b+3ab^2+b^3}\)
において
\(\color{red}{ +b の代わりに (-b) を代入するだけ}\)
なので、実は覚える必要はないです。
\(\hspace{7pt} (a-b)^3 \\
=\{a+\color{red}{(-b)}\}^3\\
=a^3+3a^2\color{red}{(-b)}+3a\color{red}{(-b)^2}+\color{red}{(-b)}^3\\
=a^3-3a^2b+3ab^2-b^3\)
でも、やはり、覚えておくと早いのかな。
というより、練習を積んでいくとどっちが自分に合っているか分かって来ます。
多くの公式を暗記して使い倒すか、
ひとつの公式をちょっとした変形を加えて使うか。
時間が限られるので「分野によって使い分ける」というのもひとつの方法ですが,
これは個人の力量によって、または指導者の方針によって変わるかもしれないですね。
一般の参考書、問題集などでは暗記しているものとして解説してあります。
変形を使うタイプの人は解答の行間を埋めるためにも別途公式を導いた後で解説を読む(読み直す)ようにしましょう。
この\((-b)\)を利用するときの公式
\( {(a-b)^3=a^3-3a^2b+3ab^2-b^3}\)
の第2項以降の符号を間違える人が多いですが、
(-b)が何乗されるか見れば分かりますので、間違えないで下さい。
私は覚えていますが、覚えていてもこれは毎回確認しながらすすめています。
で、元に戻りましょう。
(4)は
\( {(x-3)^3}\\
{=x^3+3x^2(-3)+3x(-3)^2+(-3)^3}\\
{=x^3-9x^2+27x-27}\)
または
\( {(x-3)^3}\\ \\
{=x^3-3x^2(3)+3x(3)^2-(3)^3}\\ \\
{=x^3-9x^2+27x-27}\)
もちろん結果は同じです。
ちょっと途中だけどすみません。
公式を覚えていない人が多すぎます。
単に覚えるだけではなく使えないといけませんが、基本的になる、
その場で導けない公式ぐらいは覚えておきましょう。
でなければ何もできません。
英語の単語と同じですからね。
それと、この3次の展開も8回展開すれば出てきますが、
いつまでも先に進もうとしないと後々苦しくなるので覚えた方が良いです。
簡単な例えでいうと、かけ算も足し算を繰り返せば答えは出ますが、
5×9を
5+5+5+5+5+5+5+5+5
としますか?
同じことを続けているということです。
どこまで覚えればいいか?
自分の判断で行けるところまでで良いですが、
「あるものは使う」
くらいに考えて英単語のつもりで覚えていきましょう。
英語ほど単語数が多いわけではありません。
それと、いずれ出てきますが、対称式を基本対称式で表す方法、これも覚えておきましょう。
どちらかというと、因数分解公式より基本対称式を利用する問題の方が多いくらいです。
(5)です。
\( {(2a+3b)^3}\\ \\
{=(2a)^3+3(2a)^2(3b)+3(2a)(3b)^2+(3b)^3}\\ \\
{=8a^3+36a^2b+54ab^2+27b^3}\)
これは、展開公式
\( {(a+b)^3=a^3+3a^2b+3ab^2+b^3}\)
を利用しただけです。
(6)
\( {(x-3)(x^2+3x+9)}\)
は、
\( {(a-b)(a^2+ab+b^2)=a^3-b^3}\)
そのものです。
覚えていなくても展開すれば出てきますが覚えておくと早いですね。
問題によっては「この公式」って見抜きにくいことも多いですが、慣れると使えます。
不安なときは展開して検算すれば良いのです。(時間があればだけど)
\( {(x-3)(x^2+3x+9)=x^3-27}\)
ちなみに、
\( {(a-b)(a^2+ab+b^2)=a^3-b^3}\)
は逆に見れば因数分解公式です。
全てそうですから、展開と因数分解は同時に成り立っています。
因数分解出来るなら展開はできます。
しかし、
展開がてきるなら因数分解できる、とはなりませんので注意して下さいね。
それと、
\( {(a-b)(a^2+ab+b^2)=a^3-b^3}\)
は
\( {(a+b)(a^2-ab+b^2)=a^3+b^3}\)
の \(b\) に\((-b) \)を代わりに入れただけというのも、もう説明はいらないでしょう?
代入して確認してみると納得できると思います。
これらは展開の基本です。
公式を覚えてなくてもひたすら展開すれば答えは出ますが、
因数分解にもつながりますので、
「展開公式」としても知っておいても良いのではないでしょうか?
高校数学ⅠおよびⅡの一番最初でした。
因数分解につながるように、展開、因数分解両方の公式を一覧にしておきますね。
覚えているものばかりだとは思うけど、確認しておいて下さい。
\( {(a+b)^2=a^2+2ab+b^2}\)
\( {(a-b)^2=a^2-2ab+b^2}\)
\( {(x+a)(x+b)=x^2+(a+b)x+ab}\)
\( {(ax+b)(cx+d)=acx^2+(ad+bc)x+bd}\)
\(\color{red}{ (a+b)^3=a^3+3a^2b+3ab^2+b^3}\)
\( {(a-b)^3=a^3-3a^2b+3ab^2-b^3}\)
\(\color{red}{(a+b+c)^2=a^2+b^2+c^2+2(ab+bc+ca)}\)
\( {a^2-b^2=(a+b)(a-b)}\)
\(\color{red}{a^3+b^3=(a+b)(a^2-ab+b^2)}\)
\( {a^3-b^3=(a-b)(a^2+ab+b^2)}\)
\(\color{red}{a^3+b^3+c^3-3abc=(a+b+c)(a^2+b^2+c^2-ab-bc-ca)}\)
これくらいで良いでしょう。
最後の公式は自分で証明できるかやって見てください。
たぶんですが、覚えた方がはやい、となります。笑
もう一つおまけです。
\( {x^n-1=(x-1)(x^{n-1}+x^{n-2}+x^{n-3}+\cdot\cdot\cdot+x^2+x+1)}\)
もたまに使いますので少し余裕のある人は覚えておくと良いですね。
その都度公式を導きだすのか、覚えて使うのか、模擬試験やセンター試験もちろん本試験でも大きな差となりますよ。
展開ができるようになれば逆方向の計算、
因数分解公式を覚えに行きましょう。
ずっと使います。