方べきの定理はセンター試験でも毎年問われるくらい良くでますが、公式を暗記するより覚え方を変えた方法が使えます。
円と関連した問題になりますので、先に円に内接する四角形の対角線が持つ性質を確認しておきましょう。
定理の簡単な証明をしておきますが、ここは簡単な割に出題率が高いので試験直前の対策にもなりますよ。
センター試験の図形問題において、円は必ずといって良いほど関係してきます。
これは共通テストになっても変わらないでしょう。
円に内接する四角形
先に例題をあげておきます。
パッと見た感じで分かるとは思いますが、確認しておいてください。
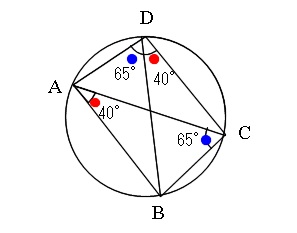
下の図において、点A.B,C,Dは円周上にある。
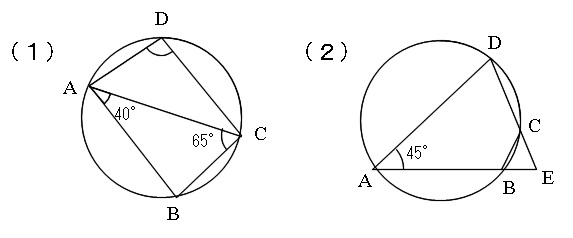
(1)∠ADCを求めよ。
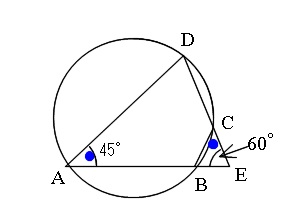
(2)ABとDCを延長した交点をEとする。
∠CEB=60°であるとき、∠CBEを求めよ。
外接円、内接円などは三角比とともに融合されてよく出てきますが、1つひとつ確認していきましょう。
例題1では角度についてです。
これは中学生でも知っている人は多いでしょう。
「円に内接する四角形の内対角の和は180°」 ・・・①
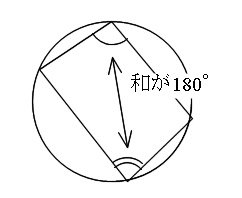
高校生ならこれは知っていて当たりまえですね。
使い道は多いので三角比の説明を見直しておいてください。
これから、
「内接四角形の1つの外角は、その対角に等しい。」 ・・・②
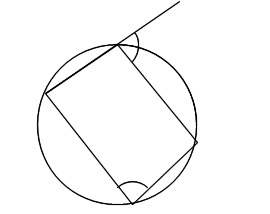
も言えます。
(1)△ABCに着目し、
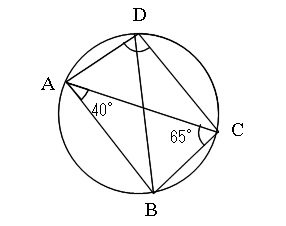
\(180-(40+65)=75\) から \( \angle {ABC}=75^\circ\)
よって①から
\(\angle {ADC}=180^\circ-75^\circ=\underline{105^\circ}\)
でも良いし、中学生みたいにDBを結び円周角の定理から、
\( \angle {ADC}\\
=\angle{ADB}+\angle{BDC}\\
=\angle{ACB}+\angle{BAC}\\
=65^\circ+40^\circ=105^\circ\)
としても良いですね。
内接四角形があれば対角線を引けば円周角の等しいところがあちこちにできます。
円周角の定理もよく使うので、復習はしておいてください。
(2)これは、②の「内接四角形の1つの外角はその対角に等しい」より

\(\angle{CBE}=\angle{ADE}\) および \( \angle{DAB}=\angle{BCE}\)
なので、どちらを利用しても答えは容易に出てきます。
\(\angle {CEB}=60^\circ\)
という条件を見逃してはダメですよ。
条件が端っこにちょこっと足されている場合もあるので、見逃すと答えまで届きません。
問題文に余計な条件はありません。
問題には必要な条件は必ずあって、過ぎる条件はほとんどありません。
たまにワナとして書かれている条件がありますが、中学校基本程度まででしょう。
例えば、
「平行四辺形」とあれば「台形」では条件が足りないからです。
「長方形」とあれば、「平行四辺形」では足りないからです。
条件はすべて使っているか、確認しながら解くと答えまでたどり着く可能性は高くなります。
解答の途中でもつまずいたら、「何か使っていない条件はないか」確認すると良いですね。
さて、答えを出しておきましょう。
三角形の内角の和から
\( \angle {CBE}=\angle{ADE}=180^\circ -(45^\circ+60^\circ)=\underline{75^\circ}\)
もちろん、
\( \angle {CBE}\\ \\
=180^\circ -\angle{BCE}-\angle{CEB}\\ \\
=180^\circ -\angle{DAB}-\angle{CEB}=75^\circ\)
でも同じです。
方べきの定理
ここも問題を先にあげておきます。
「方べきの定理を使う」問題といわれれば簡単に見えますが、いろいろと条件が与えられて、
先にに三角比の定理などを考えているので『方べきの定理』に気がつきにくいところなのです。
図のように円周上の点A,B,C,Dがあり、
ABとCDが点Pで交わっている。
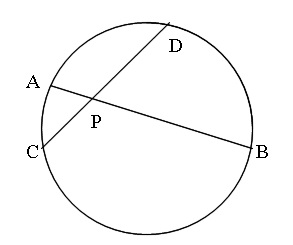
CP=2,DP=3,AB=6,AP<BPのとき、
AP,BPの長さを求めよ。
今度は「長さ」です。
長さを求める問題は、「合同」、「相似」、「三平方の定理」を使えばほとんど求まるのですが、圧倒的に「相似」が多いです。
方べきの定理の証明
【定理】
円の2つの弦AB、CDの交点、またはそれらの延長線の交点をPとすると、
\(\large{\color{red}{PA\cdot PB=PC\cdot PD}}\)
が成り立つ。
また、この逆も成り立ちます。
簡単に言えば、
「 PA・PB=PC・PD が成り立つなら4点A,B,C,Dが同一円周上にある。」です。
さて、『方べきの定理』を覚えていなくとも、
円周角の定理を覚えていれば相似な三角形
\( \triangle {APC} ∽ \triangle{DPB}\)
はすぐに分かります。
すると、
\( \color{red}{AP}:\color{blue}{DP}=\color{blue}{PC}:\color{red}{PB}=AC:DB\)
が言えるので、
\(\color{red}{PA}\cdot \color{red}{PB}=\color{blue}{PC}\cdot \color{blue}{PD}\)
これが『方べきの定理』です。
もう少しきちっと証明しておきますが、覚えて使えば良い公式です。
もし忘れたら相似な三角形をかき出せばすぐに出てきますよ。
2つに分けておきます。
【方べきの定理①】
円Oの外部の点Pから点Tで接する接線と2点A,Bで交わる直線、2点C,Dで交わる直線を引くとき
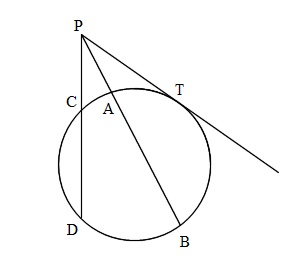
\( \large{\color{red}{PA\cdot PB=PC\cdot PD=PT^2}}\)
【方べきの定理②】
円Oの内部の点Pを通る2直線のそれぞれが、円Oと2点A,Bおよび2点C,Dで交わるとき
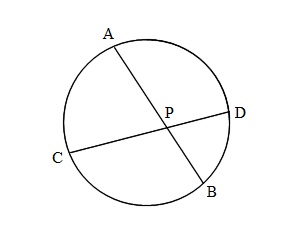
\( \large{\color{red}{PA\cdot PB=PC\cdot PD}}\)
Pが円外にあって、接線になっていない場合の公式も相似な三角形を書き出すとすぐに出てきますよ。
\( \large{\color{red}{PA\cdot PB=PC\cdot PD}}\)
関係式は同じなので覚えておいた方が早いですけどね。
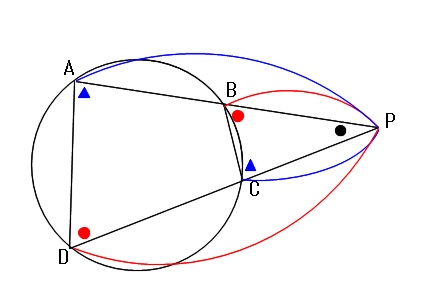
\(\triangle {PTA}\) と \( \triangle {PBT}\) において、
接弦定理より
\(\angle{PTA}=\angle{PBT}\)
また
\( \angle{P}\) は共通
よって2組の角がそれぞれ等しいから相似が言えて
\( \triangle{PTA} ∽ \triangle{PBT}\)
したがって
\( PT:PA=PB:PT\\ \\
\Leftrightarrow \hspace{10pt} PA\cdot PB=PT^2\)
\( \triangle {PAC}\) と \( \triangle {PDB}\) において、
円周角が等しいことより
\( \angle{PAC}=\angle{PDB}\)
\( \angle{PCA}=\angle{PBD}\)
よって2組の角がそれぞれ等しいから相似が言えて
\( \triangle{PAC} ∽ \triangle{PDB}\)
したがって
\( PA:PC=PD:PB\\ \\
\Leftrightarrow \hspace{10pt} PA\cdot PB=PC\cdot PD\)
相似を抜き出して線分比、というのは同じですよね。
方べきの定理を利用した問題の解き方
では、長さを求めに行きましょう。
「CP=2,DP=3,AB=6,AP<BP」
が与えられた数値および位置関係です。
\( AB=6\) から \( AP=x\) とおくと \( BP=6-x\) とおけて
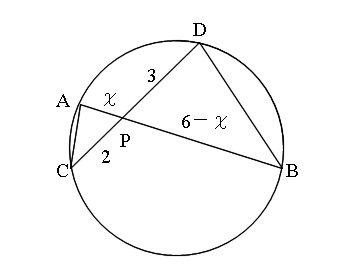
方べきの定理 \( PA\cdot PB=PC\cdot PD\) を利用すれば、
\( x(6-x)=2\cdot 3\\ \\
\Leftrightarrow \hspace{10pt} x^2-6x+6=0\\ \\
\Leftrightarrow \hspace{10pt} x=3 \pm \sqrt{3} ・・・①\)
ここで はじめて「AP<BP」が効いてきて、
\( AP=3-\sqrt{3}\)
\( BP=3+\sqrt{3}\)
①の \( x\) の値2つがAP、BPを表していることは足してみると確認出来ますよ。
ポイントは「問題分の条件はすべて使う」です。
センター試験が共通テストになっても条件の使い方は変わりません。
図形問題は三角比から復習しておくと良いです。