軌跡とは、「条件を満たす点が動ける範囲」と考えていいです。
求め方は示された条件を関係式にするだけなので難しく考えなくて良いですよ。
円でも楕円でも同じ方法でできますので、ここでは軌跡問題の代表的な放物線の頂点の軌跡と内分点の軌跡を例題に説明してみます。
軌跡の求め方の流れ
軌跡の求め方の基本的な流れは決まっています。
・求めたい軌跡の座標を \((X\,,\,Y)\) とする。
→
・ \( X\,,\,Y\) を媒介変数 \( t\) などを用いてそれぞれ表す。
→
・媒介変数を消去して \( X\,,\,Y\) の関係式を求める。
→
・問題に合わせて \( (x\,,y)\) 座標で関数として表し、グラフなどにする。
それだけですが、範囲があることが多いので注意しておきましょう。
早速例題に入りましょう。
放物線(2次関数)の頂点の軌跡を求める問題
放物線 \( y=x^2-2(m+1)x+3m^2-m\) において、\( m\) が変化するとき、
頂点のえがく軌跡を求め、そのグラフを書け。
放物線の頂点に関しては2次関数の分野で十分練習しているでしょう。
平方完成しなければ始まりませんよね。
放物線を表している2次関数を平方完成します。
\( y=x^2-2(m+1)x+3m^2-m\\ \\
=\{x-(m+1)\}^2-(m+1)^2+3m^2-m\\ \\
=\{x-(m+1)\}^2-m^2-2m-1+3m^2-m\\ \\
=\{x-(m+1)\}^2+2m^2-3m-1\)
から、頂点の座標は
\( (m+1\,,\,2m^2-3m-1)\)
です。
ここまでは良いのですが、気をつけておいて欲しいのは、
元の放物線と、この後の関係式から出てくる放物線は別物
だということです。
後で出てくる放物線は「頂点の軌跡がたまたま放物線だった」というだけです。
頂点の \( x\) 座標を \(X\) ,\( y\) 座標を \( Y\) とすると、
\( X=m+1\) ・・・①
\( Y=2m^2-3m-1\) ・・・②
①から \( m=X-1\) として②に代入すると、
\( m\) を消去して \( X\,,\,Y\) の関係式が作れます。
\( Y=2(X-1)^2-3(X-1)-1\\ \\
=2(X^2-2X+1)-3(X-1)-1\\ \\
=2x^2-4X+2-3X+3-1\\ \\
=2X^2-7X+4\\ \\
=2\left(X^2-\displaystyle \frac{7}{2}X\right)+4\\ \\
=2\left\{\left(X-\displaystyle \frac{7}{4}\right)^2-\displaystyle \frac{49}{16}\right\}+4\\ \\
=2\left(X-\displaystyle \frac{7}{4}\right)^2-\displaystyle \frac{49}{8}+\displaystyle \frac{32}{8}\\ \\
=2\left(X-\displaystyle \frac{7}{4}\right)^2-\displaystyle \frac{17}{8}\)
※
問題集や参考書ではこの式変形の途中はところどころ省略されます。
行間は自分で計算して埋めるんですよ。
出てきた関係式は \( XY\) の関係式なので、\( xy\) に軸を変えて、
求める軌跡は
\( \underline{y=2\left(x-\displaystyle \frac{7}{4}\right)^2-\displaystyle \frac{17}{8}}\)
グラフは、図のようになります。
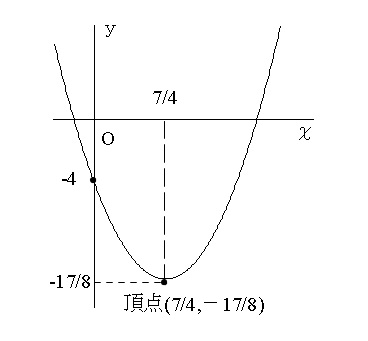
求めた頂点の軌跡の放物線を \( xy\) 軸で表現しているだけで、
軌跡の求め方は、
「 \( X\,,\,Y\) でまずは関係式を出す」
という方向性は変わりません。
注:放物線のグラフは、基本3点, 頂点が分かっている場合はあと1点で定まります。
軌跡問題では、
「求める軌跡上の点を \( (X\,,\,Y)\) と置く。」
というのを基本として、媒介変数(ここでは \( m\) )を消し、
\( (X\,,\,Y)\) の関係式を作っていくことを覚えてください。
求める軌跡上の点は \( (x\,,\,y)\) でも良いのですが、
元の関数の \( x\,,\,y\) と同じなので紛らわしいから一旦違う文字で置きかえて、
再度 \( xy\) 座標で表すのです。
線分を内分する点の軌跡を求める問題
点P \( (-1\,,\,-3)\) と曲線 \( y=x^2-4x+3\) 上を動く点Qとを結ぶ線分PQを、
2:1に内分する点Rの軌跡を求めよ。
例題1のように関係式を作り出すだけで処理することも出来ますが、少しイメージしておきましょう。
「軌跡」はある条件を満たす点の集まった曲線である、ということを忘れないで下さい。
ちなみに、通常「曲線」とは「直線」も含みますのでご注意を!
点P \((-1\,,\,-3)\) と \( y=x^2-4x+3\) 上の点Qを結ぶ線分は、点Qが動きますので変化しています。
その内分点Rも動きます。
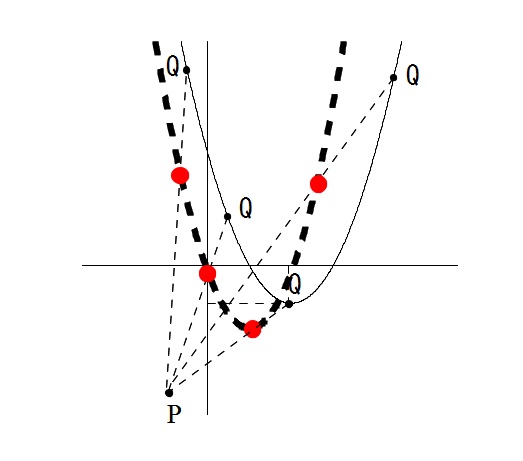
手書きで、簡単にで良いんです。
だいたいどんな感じかなあ?程度でいいので、概図でみておきます。
時間はそれほどかかりません。
線分PQを2:1に内分する点Rの軌跡は、
「放物線」
と、までは推測出来ます。
(ある程度推測できるまで点を打ってみると良いですね。)
後は代数的に処理するだけです。
求める軌跡上の点Rを \( (X\,,\,Y)\) とし、
点Qの \( x\) 座標を \( t\) とおくと点Qの座標は
\( (t\,,\,t^2-4t+3)\)
となり、
線分PQを \( 2:1\) に内分する点Rは、
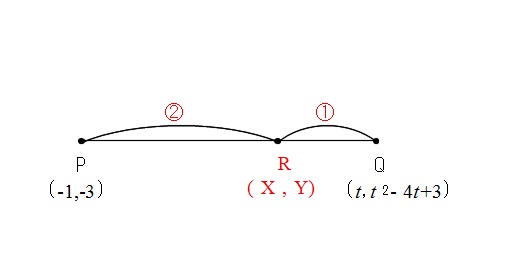
\( X=\displaystyle \frac{-1+2t}{2+1}=\displaystyle \frac{-1+2t}{3}\)
\( Y=\displaystyle \frac{-3+2(t^2-4t+3)}{2+1}=\displaystyle \frac{2t^2-8t+3}{3}\)
を満たします。
これらから \( t\) を消去します。
少しややこしいけどこれくらいは処理できるようになりましょう。
\(3X=-1+2t\) より
\(\displaystyle 2t=3X+1 \Leftrightarrow t=\frac{3X+1}{2}\)
これをYに代入して、
\( Y=\displaystyle \frac{1}{3}\left\{2\left(\displaystyle \frac{3X+1}{2}\right)^2-8\left(\displaystyle \frac{3X+1}{2}\right)+3\right\}\\ \\
=\displaystyle \frac{1}{3}\left\{2\left(\displaystyle \frac{9X^2+6X+1}{4}\right)-4(3X+1)+3\right\}\\ \\
=\displaystyle \frac{1}{3}\left(\displaystyle \frac{9X^2+6X+1}{2}-12X-4+3\right)\\ \\
=\displaystyle \frac{1}{3}\left(\displaystyle \frac{9X^2}{2}+3X+\displaystyle \frac{1}{2}-12X-1\right)\\ \\
=\displaystyle \frac{1}{3}\left(\displaystyle \frac{9X^2}{2}-9X-\displaystyle \frac{1}{2}\right)\\ \\
=\displaystyle \frac{3}{2}X^2-3X-\displaystyle \frac{1}{6}\)
これを \( xy\) 座標系に直して
\( \underline{y=\displaystyle \frac{3}{2}x^2-3x-\displaystyle \frac{1}{6}}\)
計算力強化のため、確かめて下さい。
計算過程を少し見やすくすることもできます。
\(\displaystyle X=\frac{-1+2t}{3} \Leftrightarrow 2t=3X+1\)
を代入するとき
\( Y=\displaystyle \frac{2t^2-8t+3}{3}\\ \\
=\displaystyle \frac{4t^2-16t+6}{6}\\ \\
=\displaystyle \frac{(2t)^2-8(2t)+6}{6}\\ \\
=\displaystyle \frac{(3X+1)^2-8(3X+1)+6}{6}\\ \\
=\displaystyle \frac{9X^2+6X+1-24X-8+6}{6}\\ \\
=\displaystyle \frac{9X^2-18X-1}{6}\\ \\
=\displaystyle \frac{3}{2}X^2-3X-\displaystyle \frac{1}{6}\)
こんな変形をできれば少しは計算が見やすくなりますけど、試験場で気がつくかどうかです。
領域の図示問題は軌跡とセットです。
⇒ 領域:連立不等式の範囲を図示する方法と格子点と面積の求め方
共通テストはマークだからない?
図を選択する方法なら出題できますよ。
要点は定期テストでも使えますよ。
基本を幅広く抑えておくこと、それが一番の対策になります。