ベン図を使った集合問題の解き方とドモルガンの法則

集合問題でベン図を使って解きなさいという問題はあまり見ませんが、
実はベン図を使うと楽に求めることができる問題は少なくありません。
要素が２つの場合は小学生や中学生でも使うでしょうが３つの場合の解き方もあります。
ここではベン図を利用して基本的な作業をすればド・モルガンの法則も覚える必要はないと言うところまでを説明します。

ベン図とは

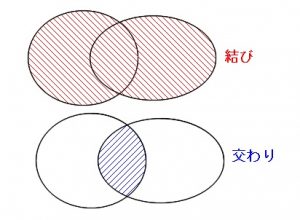
ベン図とは、集合の「交わり」や「結び」などを視覚的に説明するときに使われる図のことです。

集合の用語や記号の復習はしておいてください。

⇒　集合の記号と意味（要素,真部分集合,和集合,補集合,ド・モルガンの法則など）

覚えていないと問題の意味さえ分からないと言うことになりますよ。

簡単な集合要素の問題

集合要素が２つの場合は簡単ですね。
ベン図を書いてもすっきりとしてます。

「結び」は\(\hspace{4pt}A\,\color{blue}{\cup}\, B\hspace{4pt}\)です。
　
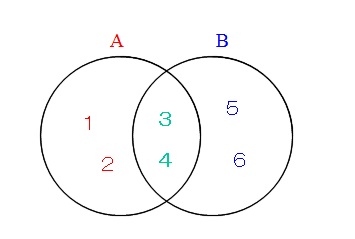
　\(\hspace{10pt} A\cap B=\{3,4\}\)

少し数を多くしてみます。

　\( A\cap B\,,\,A\cup B\)
は集合を表していますが
　\( \color{red}{ n}(A\cap B)\,,\,\color{red}{ n}(A\cup B)\)
は集合要素の「数」（「number」）を表しています。

数学の記号には書かなくても通用する意味がありますので、
忘れないように確認しておいてくださいね。

センター試験では教科書にある言葉の定義も、
問題に書いてくれている親切すぎる問題もありますが、
共通テストでいつもある訳じゃないので気をつけておきましょう。

この問題は数えても\(\,100\,\)個しかありません。
でも、試験時間を考えると数え上げるのはちょっともったいないです。

倍数の性質と、ベン図を利用しましょう。

\(\,100\,\)までの自然数の中には
\(\,2\,\)の倍数は\(\,50\,\)個、\(\,3\,\)の倍数は\(\,33\,\)個あります。

　\(\hspace{10pt} n(A)=50\,,\,n(B)=33\)

でも、この中には重ねて数えている数字もあります。
\(\,2\,\)と\(\,3\,\)の公倍数である\(\,6\,\)の倍数です。

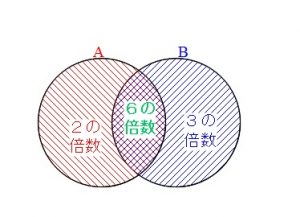
だから重なっている数を１回引いておかないと合いません。

　\( n(A\cup B)=n(A)\,+\,n(B)\,-\,\color{red}{ n(A\cap B)}\)

\(\,6\,\)の倍数は
　\(\hspace{10pt} 6\,,\,12\,,\,18\,,\cdots \,,\,96(=6\times 16)\)
だから
　\(\hspace{10pt} n(A\cap B)=16\)
であるということと、同時にもう一つの答もでます。

　\(\begin{eqnarray} n(A\cup B)&=&50+33-16\\
&=&67\end{eqnarray}\)

これはベン図に要素の数を書き込めば確認できます。
（注意：普通はベン図には要素の数ではなく要素を書きます。）

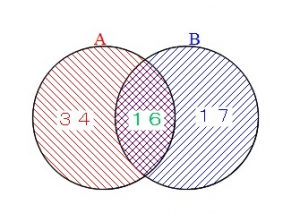
\(\,2\,\)の倍数で\(\,6\,\)の倍数ではないのは\(\,34\,\)個、
\(\,3\,\)の倍数で\(\,6\,\)の倍数ではないのは\(\,17\,\)個、
\(\,6\,\)の倍数は\(\,16\,\)個、
合わせると\(\,67\,\)個で同じです。

３つ集合要素の個数をベン図で数える方法

集合要素が３つの場合の例題をあげて説明します。

基本的な計算式をあげておきます。

集合\(\,A\,\)の要素の個数を
　\( n(A) \)
などと表すことにします。

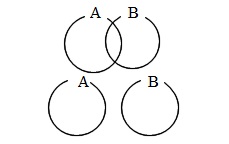
和集合の要素の個数：
　\( n(A\cup B) = n(A)\,+\,n(B)\,-\,\color{red}{ n(A \cap B)}\)
（重なり部分 Ａ∩Ｂ は２回足されているので１回引く）

ただし、\( (A\cap B)= \phi \) (空集合)　のときは
　\( n(A \cup B)=n(A)\,+\,n(B)\)

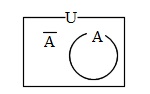
補集合の要素の個数：
集合全体の数を\(\hspace{4pt}n(U)\hspace{4pt}\)とすると
　\(\hspace{10pt} \overline{A} = n(U) – n(A) \)
（　\(\overline{A}\hspace{4pt}\)は集合\(\,A\,\)の補集合です。　）

３つの集合の和集合の要素の個数：
　\(\hspace{10pt} n(A\cup B\cup C)\\
=n(A)\,+\,n(B)\,+\,n(C)\\
\hspace{20pt}-\,n(A\cap B)\,-\,n(B\cap C)\,-\,n(C\cap A)\\
\hspace{30pt}+\,n(A\cap B\cap C)\)
ですが、
上に示したようにベン図（確かジョン・「ベン」さんという人の名前から取った）
で確認した方が確実で早いです。

補集合のド･モルガンの法則もベン図ならすぐ示せるし、
ベン図を書けばややこしい式を覚える事なく解答できるので、
ベン図を書くことをお勧めします。

ただし、ベン図では要素（要素の数ではなく）を書き入れることが原則です。
解答上に示すのではなく、自分で要素の数だけを確認するのに利用するのは問題ありません。

さて、
　\(\hspace{10pt} n(A\cup B\cup C)\\
=n(A)\,+\,n(B)\,+\,n(C)\\
\hspace{20pt}-\,n(A\cap B)\,-\,n(B\cap C)\,-\,n(C\cap A)\\
\hspace{30pt}+\,n(A\cap B\cap C)\)
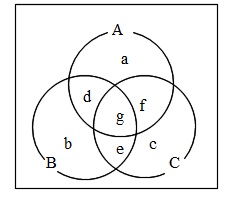
をベン図で表すと、下図のようになり、
　\(\hspace{10pt}\,a\,,\,b\,,\,\,c\,,\,d\,,\,e\,,\,f\,,\,g\,\)
はそれぞれ区切られた部分の要素の個数を表しています。

　\(\hspace{10pt} n(A\cup B\cup C)\\
=\,a\,+\,b\,+\,c\,+\,d\,+\,e\,+\,f\,+\,g \)

　\( n(A\cap B\cap C)=\,g\)

（他も要素の個数を出して確認してみて下さい。)

\(\,g\,\)は３回重なっているのですが、
上の式では３回引かれてなくなっていますので、
一回足し直しているのです。

式に頼る場合はその点が注意ですね。

ここでは、ベン図に要素の数をすべて書き込んで見ます。
（書き込みしてある数字は要素ではなく要素の数です。）

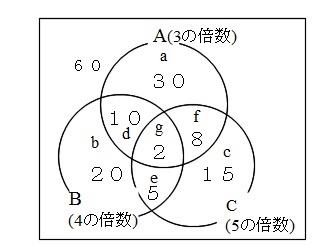
小学生みたいだけど、確実なことが分かります。

\(\,150\,\)までの数の中には、
\(\,A\,\)：（３の倍数）\(\,50\,\)個
　\( (a+d+f+g)\)

\(\,B\,\)：（４の倍数）\(\,37\,\)個
　\( (b+d+e+g)\)

\(\,C\,\)：（５の倍数）\(\,30\,\)個
　\( (c+e+f+g)\)

\(\,A∩B\,\)：（１２の倍数）\(\,12\,\)個
　\( (d+g)\)

\(\,B∩C\,\)：（２０の倍数）\(\,7\,\)個
　\( (e+g)\)

\(\,C∩A\,\)：（１５の倍数）\(\,10\,\)個
　\( (g+f)\)

\(\,A∩B∩C\,\)：（６０の倍数）\(\,2\,\)個
　\( (g)\)

これをベン図に要素の個数として「 \(\,g\,\) 」から逆に書き込んでいくと、
　\(\hspace{10pt} g=2\,,\,f=8\,,\, e=5\,,\, d-10\,,\\
c=15\,,\,b=20\,,\, a=30 \)

よって、
　\(\hspace{10pt} n(A\cap B\cap C)=2 \)

　\(\begin{eqnarray} n(A\cup B\cup C)&=&2+8+5+10+15+20+30\\
&=&90\end{eqnarray}\)

書き込む数字は多くなりますが、式では到底あつかえません。
ベン図を使えば、単純な足し算引き算ですよね。

まとめ

ド・モルガンの法則は覚えられる人は覚えて使えれば良いと思います。

ド・モルガンの法則

　\(\large{ \color{red}{ \overline{A\cup B}=\overline{A}\cap \overline{B}}}\)
　\(\large{ \color{red}{ \overline{A\cap B}=\overline{A}\cup \overline{B}}}\)

でも式自体を覚えるのに時間がかかり、
数学が面白くない、と感じるようであれば、ベン図を書いて処理することをお勧めします。

論理は確かに大切ですが、ここで数学が嫌いになっては後が続きません。

最初の内は楽しめる範囲で答えを出しておいて、
余裕が出来てからド・モルガンなどの法則を式で覚えて行けばいいと思いますよ。

⇒　集合の記号と意味（要素,真部分集合,和集合,補集合,ド・モルガンの法則）

集合で使う記号のチェックはしておいた方が良いです。
忘れている人結構いますよ。

⇒　数と式（高校数学Ⅰ）の要点

集合と命題は数学\(\,Ⅰ\,\)範囲に入っている共通テストでも必須項目です。