二項定理は意味よりも公式化されたものを暗記しているのではないでしょうか。
しかし、公式の形がシグマで表されているので覚えにくく使えない状態の人が多くいます。
一般項の見方と2項展開したときの係数の求め方を具体的な問題を使って説明しておきます。
二項定理
【定理】
\( n\) を自然数とするとき、
\(\displaystyle (a+b)^n = \sum_{k=0}^n \,{_n\mathrm{C} _k} \,a^{n-k}\,b^k \)
このとき \( _n\mathrm{C}_0=1\) とします。
しかし、このシグマで表された公式では覚えにくいし分かりにくいので、具体的にかき出しておけば良いのです。
例えば、
\( (a+b)^3=a^3+3a^2b+3ab^2+b^3\)
この各項の次数と係数はパスカルの三角形で求まります。
その係数を順番に
\( 1=_3\mathrm{C}_\color{red}{0}\,,\,3=_3\mathrm{C}_\color{red}{1}\,,\,3=_3\mathrm{C}_\color{red}{2}\,,\,1=_3\mathrm{C}_\color{red}{3}\)
とあてはめて
\( \displaystyle (a+b)^3=_3\mathrm{C}_\color{red}{0} a^3b^\color{red}{0}+_3\mathrm{C}_\color{red}{1} a^2b^\color{red}{1}+_3\mathrm{C}_\color{red}{2} a^1b^\color{red}{2}+_3\mathrm{C}_\color{red}{3} a^0b^\color{red}{3}\\ \\
\displaystyle =\sum_{k=0}^3 \,{_3\mathrm{C} _\color{red}{k}}\, a^{3-k}\,b^\color{red}{k}\)
のように一般化していけば公式のまま覚える必要はありません。
といってもまだ分かりにくいという人のために、もう少し詳しく具体的な説明をしておきます。
ただ、パスカルの三角形は使えるようにしておいた方が分かり易いです。
2項展開の係数と次数の関係
もう一度二項定理を一般化してみますが、
その前に、「パスカルの三角形」に触れておきます。
\( (a+b)^1=a+b\)
\( (a+b)^2=a^2+2ab+b^2\)
\( (a+b)^3=a^3+3a^2b+3ab^2+b^3\)
と続きますが、係数だけを見ていくと、
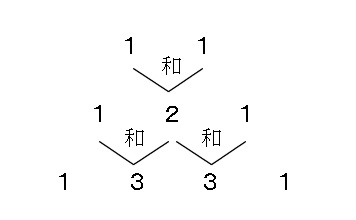
となっています。(左右端は1です)
この後も続くのですが、項の次数がどうなっているのかを見てみると、
\( a\) については次数が1つずつ下がっていき、
\( b\) については1つずつ上がっていきます。
ただし、すべての項の次数は、同じで \( (a+b)^n\) の場合 \( n\) 次となります。
例えば、
\( (a+b)^3=a^3+3a^2b+3ab^2+b^3\)
ではすべての項は3次です。
つまり \( (a+b)^n\) を展開したときの項は、
\( a^nb^0\,,\,a^{n-1}b^1\,,\,a^{n-2}b^2\,,\,\cdots,a^{n-k}b^k\,,\cdots\,a^1b^{n-1}\,,\,a^0b^n\)
\( a,b\) の次数は順に
\( a \hspace{5pt}\Rightarrow \hspace{5pt}a^n\,,\,a^{n-1}\,,a^{n-2}\,,\, \cdots ,a^{n-k},\cdots\, ,\,\hspace{5pt}a^1\hspace{5pt},\hspace{5pt} a^0 \)
\( b \hspace{5pt}\Rightarrow \hspace{5pt}b^0\hspace{5pt},\hspace{10pt} b^1\hspace{8pt},\hspace{10pt}b^2\hspace{5pt}, \cdots\hspace{5pt},\hspace{5pt}b^k\hspace{5pt}, \cdots, b^{n-1}\,,\, b^n\)
となっており、係数はパスカルの三角形で考えていくと、
\( _n\mathrm{C}_0\,,\,_n\mathrm{C}_1\,,\,_n\mathrm{C}_2\,,\,\cdots\,,\,_n\mathrm{C}_k\,,\,\cdots \,,\,_n\mathrm{C}_{n-1}\,,\,_n\mathrm{C}_n\)
\( a\) と \( b\) が全部で \( n\) 個並んでいる中に、
\( \color{red}{k}\) 個の \(\color{red}{ a}\) をどこに何個置くかの並べ方なので、
\( \color{red}{_n\mathrm{C}_k}\)
と考えても良いです。
合わせて表現すると、
\( _n\mathrm{C}_0=1\,,\,_n\mathrm{C}_n=1\,,\,a^0=1\,,\,b^0=1\)
であることから、
\( (a+b)^n\\ \\
=_n\mathrm{C}_0\cdot a^nb^0+_n\mathrm{C}_1\cdot a^{n-1}b^1+\cdots +_n\mathrm{C}_k\cdot a^{n-k}b^k+\cdots+_n\mathrm{C}_{n-1}\cdot a^1b^{n-1}+n\mathrm{C}_n\cdot a^0b^n\)
これが二項定理(Σは使っていません)で \( \color{red}{_n\mathrm{C}_k\cdot a^{n-k}b^k}\) を一般項といいます。
二項定理を利用して係数を求める問題
式
\(\displaystyle\left( x-\frac{1}{2x}\right)^9\)
を展開したとき、\( x^3\) の項の係数を求めよ。
「 \( x^3\) の項の係数を求めよ」
なので一般項 \( _n\mathrm{C}_k\cdot a^{n-k}b^k\) に当てはめてみましょう。
\( n=9\) で,\( k\) を求めに行くとして、
\( a=x \hspace{5pt},\hspace{5pt} b=(-2x)^{-1}\) を一般項に入れます。
(符号や係数もそのまま入れて下さい、)
すると一般項(第 \( k\) 項)は、
\( _9\mathrm{C}_k\cdot (x)^{9-k}\left\{(-2x)^{-1}\right\}^k\\ \\
=_9\mathrm{C}_k\cdot (x)^{9-k}(-2)^{-k}(x)^{-k}k\\ \\
=_9\mathrm{C}_k\cdot (-2)^{-k} \left(x^{9-k-k}\right)\\ \\
=_9\mathrm{C}_k\cdot (-2)^{-k} \left(x^{9-2k}\right)\)
この \(x\) の指数が \( 9-2k=3\)、
つまり \(k=3\) のときが \( x^3\) の項です。
\( k=3\) のとき係数 \( _9\mathrm{C}_k\cdot (-2)^{-k}\) は、
\(~\,\hspace{10pt}_9\mathrm{C}_3\cdot (-2)^{-3}\\ \\
=\,_9\mathrm{C}_3\cdot (-8)^{-1}\\ \\
\displaystyle =\,\frac{9\cdot 8\cdot 7}{3\cdot 2\cdot 1}\cdot \left(-\frac{1}{8}\right)=\underline {-\frac{21}{2}}\)
となります。
一般項(第 \( k\) 項)の \( k\) を指数に合わせるように求めることが第一段階になりますね。
※
\(\displaystyle \frac{1}{2x}=(2x)^{-1}\) と分数は指数に直して計算しています。
この方が全体の指数が見やすいですよ。
相加相乗平均と二項定理は忘れた頃にやってくる!
多項定理は二項定理の応用ともいえるので工夫すれば覚えなくても使えますが、
二項定理は忘れないように復習しておいた方が良いですよ。
