領域とは軌跡のうち面積を持つもの、と考えて良いです。
連立不等式の範囲として図示する場合が多く、格子点や面積を求める問題も多く出題されます。
領域でのポイントは不等式の処理と図示がポイントになるので、両方ともに基本ができていないと答まで到達出来ません。
軌跡から領域へ
「軌跡」では条件を満たす点の集まりとして曲線をイメージしていれば良かったのですが、
実は軌跡を広い範囲でみると曲線だけでなく面の一部を表すこともあります。
1つの軌跡ともう一つの軌跡で囲まれる範囲、それが「領域」です。
ほとんどは連立不等式で挟まれた範囲になりますので、連立不等式で表された領域の基本的な問題を取り上げて説明しておきます。
次の不等式を満たす格子点を求めよ。
(1) \( 4x-y>0\,,\,x-3y< 0\,,\,3x+2y-11< 0\)
(2) \( x^2+y^2< 5\,,\,2x-3y+4< 0\)
格子点とは
「格子点」とは、
座標の \( x\,,\,y\) がともに整数の点のことです。
格子点や格子点の数を求めるときは、まずはグラフを書き、具体的に座標上でみていった方が良いです。
計算で出そうとするとかなり難しくなりますよ。
(1)\( 4x-y>0\,,\,x-3y< 0\,,\,3x+2y-11< 0\)
を座標上で図示すると
\( 4x-y>0\hspace{5pt} \Leftrightarrow \hspace{5pt} y< 4x\) \( x-3y< 0\hspace{5pt} \Leftrightarrow \hspace{5pt} y>\displaystyle \frac{1}{3}x\) \( 3x+2y-11< 0\hspace{5pt} \Leftrightarrow \hspace{5pt} y< -\displaystyle \frac{3}{2}x+\displaystyle \frac{11}{2}\) からこれが示す領域は図の斜線部分となります。
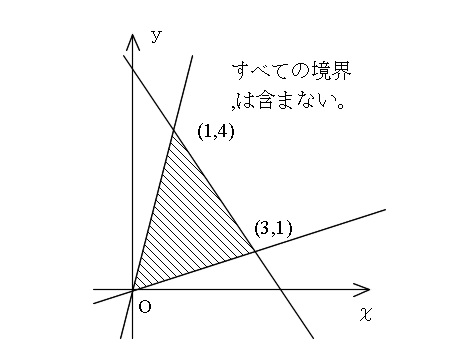
これだけみても格子点の数は分かりません。
ここでは格子点の個数ではなく、そのものをすべて求めるのだからそれほど多くはないはずですが、それでも微妙な点もあるので1つひとつ調べていくことが大切になります。
\( 4x-y=0\\ \\
x-3y=0\\ \\
3x+2y-11=0\)
の交点は
\( (0\,,\,0)\,,\,(1\,,\,4)\,,\,(3\,,\,1)\)
領域は明らかに第一象限で \( x\) 座標は正だから、
\( x=1\) の場合からみていけば良いのです。
\( x=1\) のとき、
\( (1\,,\,1)\,,\,(1\,,\,2)\,,\,(1\,,\,3)\)
は領域内にあります。
\( (x\,,\,y)=(1\,,\,4)\) は境界上(交点)なので含まれません。
元の領域が境界を含んでいないことは忘れないでください。
\( x=2\) のとき、
\( (2\,,\,1)\,,\,(2\,,\,2)\)
\( 3+2y-11<0\) を \( (2\,,\,2)\) は満たしているけど、
\( (2\,,\,3)\) は \( 3x+2y-11<0\) を満たしません。
\( x=3\) のとき \( (3\,,\,1)\) は交点なのでこの場合、領域外となります。
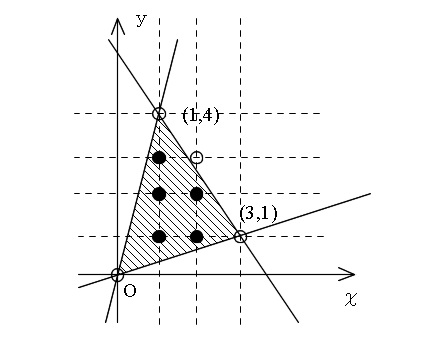
よって格子点は以上で、
\( \underline{(1\,,\,1)\,,\,(1\,,\,2)\,,\,(1\,,\,3)\,,\,(2\,,\,1)\,,\,(2\,,\,2)}\)
の5つです。
格子点問題のコツは、図示して格子点をはっきり「●」で記すことです。
これって地味だけど重要で過去に東大でも格子点の問題は出てますが、この作業によって切り開けました。
領域の示す範囲
(2)
\( x^2+y^2< 5\) ・・・①
は中心が原点、半径が \( \sqrt{5}\) の円の内部です。
\( 2x-3y+4< 0\) ・・・②
は
\( 2x-3y+4< 0\\ \\ \hspace{5pt} \Leftrightarrow \hspace{5pt} 3y>2x+4\\ \\ \hspace{5pt} \Leftrightarrow \hspace{5pt} y>\displaystyle \frac{2}{3}x+\displaystyle \frac{4}{3}\) とすればわかるように \( 2x-3y+4=0\) より上の範囲を示しています。
いずれも境界は含みません。
グラフで示すと図の様になります。

\( \sqrt{5}=2.236\cdots\)
であること、および①②を連立した交点から、
\( -2≦ x < 1\) の範囲の格子点を調べます。 つまり \( x=\color{red}{-2}\,,\,\color{red}{-1}\,,\,\color{red}{0}\) の3つ場合です。 \( \color{red}{x=-2}\) のとき
\( y=0\) は \( 2x-3y+4=0\) となり②を満たさないのでダメ。
\( y≧ 1\) は \( x^2+y^2≧ 5\) となるので①を満たさずダメ。 よって、\( x=-2\) のときはありません。 \(\color{red}{ x=-1}\) のとき
\( y=0\) は明らかにダメ。
\( y=1\) は①②ともに満たす。
\( y≧ 2\) は①を満たさないのでダメ。
\( \color{red}{x=0}\) のとき
\( 2x-3y+4=0\) の切片から \(\displaystyle \frac{4}{3}< y <\sqrt{5}\) なので
\( y=2\) のときのみで①②を満たす。
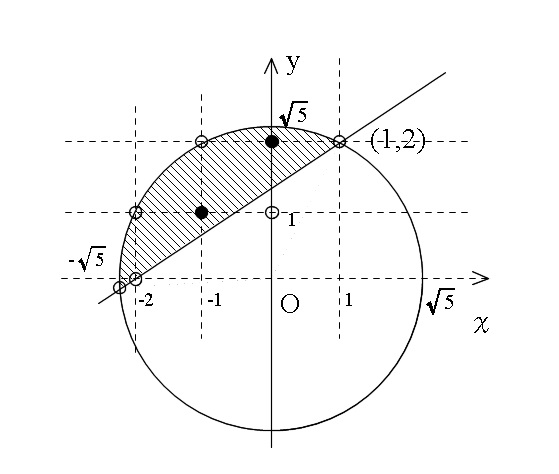
以上より、求める格子点はふたつで、
\( \underline{(0\,,\,2)\,,\,(-1\,,\,1)}\)
となります。
格子点は \(x\) 座標も \( y\) 座標も整数であるということから、境界に気をつけて「●」を付けて行く作業を手を抜かずやれば、図を見ながらだいたいの点は調べることもできますよ。
領域の面積
次の連立方程式の表す領域の面積を求めよ。
\( \begin{cases}
\hspace{10pt} (x-y)(x+y-6)≦ 0 \\ \\
\hspace{10pt} (x-3)^2+(y-3)^2≦ 18
\end{cases}\)
連立不等式の示す領域です。
第一不等式ですが、\( ab≦0\) は、
「 \( \color{red}{a≧ 0}\) かつ \( \color{red}{b≦ 0}\) 」 または「 \(\color{red}{a≦ 0}\) かつ \(\color{red}{ b≧ 0}\) 」
の二通り考えられます。これさえ注意すれば問題ありません。
\( (x-y)(x+y-6)≦ 0\) は
\( (x-y)≧ 0\) かつ \( (x+y-6)≦ 0\)
または
\( (x-y)≦ 0\) かつ \( (x+y-6)≧ 0\)
もう少し見やすくすると
\( \color{red}{y≦ x}\) かつ \( \color{red}{y≦ -x+6}\)
または
\( \color{red}{y≧ x}\) かつ \( \color{red}{y≧ -x+6}\)
で示す領域は図のようになります。
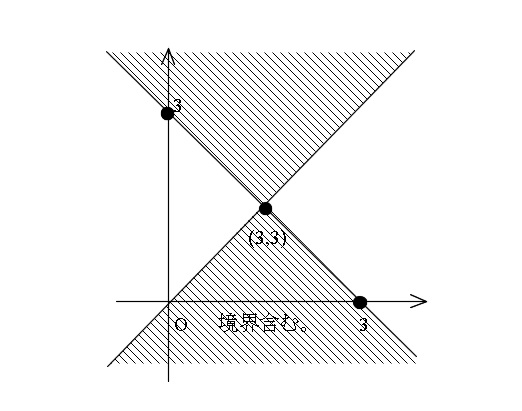
第二不等式 \( (x-3)^2+(y-3)^2≦ 18\) は
中心が \( (3\,,\,3)\) 半径が \( 3\sqrt{2}\) の境界を含んだ円の内部です。
第一不等式と合わせて図示すると、下図の領域となります。
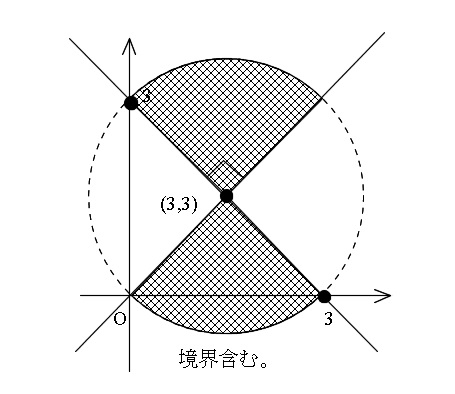
この領域は、二直線が直交していることから
半径が \( 3\sqrt{2}\) の「四分円2つ分」です。
つまり半円ということです。
よって求める領域の面積は、
\( \displaystyle \frac{1}{2}\pi(3\sqrt{2})^2=\underline{9\pi}\)
サクッと領域を示して、どのような形になるかグラフ(図)でだいたいのイメージを取れば難しくはないでしょう?
式だけ眺めてても、何も変わりません。
まずは「分かることだけでも」書き出して見ると、そこから見えてくることがたくさんあるのです。
領域と最大値最小値も良く出題されます。
が、グラフさえ書ければ何とかなります。
軌跡の求め方から見直しておくと良いですね。