図形と方程式の要点

「図形と方程式」というあいまいな表現の単元ですが、今後の数学にとって重要な数学Ⅱの単元の1つです。
点と直線、円、軌跡と領域という3つの項目に分けてまとめておきます。
この単元で出てくる図形は主に直線と円ですが、内容の応用範囲は広いですよ。

図形と方程式

ここで扱う図形は点、直線、円が主になります。
直線と円の位置関係や領域を座標上で示していきますが、
他の分野でも使う用語は多いですし、座標が関係する関数や図形すべてに通じる項目だと考えておきましょう。

点と直線

点や直線はすでに知っている用語ですが、新しい用語が加わりますのでできるだけ基本からまとめます。
座標や図形の方程式を考えるときは出てくる文字はすべて実数の範囲で考えます。

直線上の点

内分、外分を分かり易くするために先ずは数直線上の点について見ていきます。

\(\color{red}{\fbox{　数直線上の分点の座標の公式　}}\)
　数直線上の異なる\(\,2\,\)点\(\,\mathrm{A}\,(\,a\,)\,,\,\mathrm{B}\,(\,b\,)\,\)に対し、
　線分\(\,\mathrm{AB}\,\)を\(\,m:n\,\)に分ける点\(\,\mathrm{P}\,\)の座標\(\,p\,\)は
　\(\hspace{10pt}\displaystyle\color{red}{ p=\frac{na+mb}{m+n}}\)
　で与えられる。
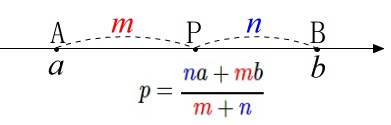ここで使っている\(\,m\,,\,n\,\)は正の数です。

最初は点\(\,\mathrm{A}\,(\,a\,)\,,\,\mathrm{B}\,(\,b\,)\,\)のような表し方に慣れていないかもしれませんが、
\(\,x-y\,\)平面座標の場合の点の座標を\(\,\mathrm{A}\,(\,x\,,\,y\,)\,\)と表す代わりに、
数直線上では\(\,x\,\)座標しかないので\(\,\mathrm{A}\,(\,x\,)\,\)としているようなものです。

特に覚えておいた方が良いのは\(\,m=n=1\,\)のときの

　中点の座標　\(\displaystyle \color{red}{\frac{a+b}{2}}\)

ですね。

内分点は線分\(\,\mathrm{AB}\,\)の間にありますが、
外分点は線分\(\,\mathrm{AB}\,\)の外側になります。

\(\,m,n\,\)を正の数として
　\(\,m＞n\,\)なら、線分\(\,\mathrm{AB}\,\)の\(\,\mathrm{B}\,\)側の延長上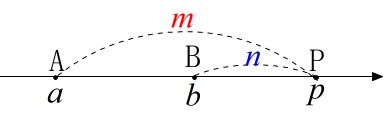
　\(\,m＜n\,\)なら、線分\(\,\mathrm{AB}\,\)の\(\,\mathrm{A}\,\)側の延長上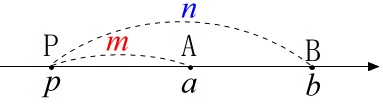
になります。

\(\color{red}{\fbox{　内分点と外分点　}}\)

線分\(\,\mathrm{AB}\,\)を\(\,m:n\,\)に外分する点とは
　\(\,m:(-n)\,\)に内分する点

のことです。
計算で求める場合はこの形で形式的に覚えておけば良いですよ。

図形上で「位置関係がわかりにくい」という人がいますが、
　「点\(\,\mathrm{P}\,\)は線分\(\,\mathrm{AB}\,\)を」
という場合、内分点でも外分点でも、
　\(\,\mathrm{A}\,\)で始まり\(\,\mathrm{P}\,\)を経由して最終的に\(\,\mathrm{B}\,\)にたどり着く順
で考えれば良いのです。

平面上の点

\(\color{red}{\fbox{　象限　}}\)

　平面座標を軸で\(\,4\,\)分割したそれぞれを
　　第\(\,1\,\)象限,第\(\,2\,\)象限,第\(\,3\,\)象限,第\(\,4\,\)象限
　という。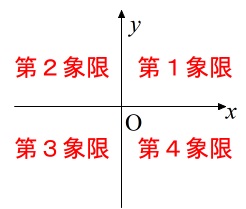\(\,x,y\,\)座標とも正となる象限を第\(\,1\,\)象限とし、
反時計回りに、第\(\,2\,\)、第\(\,3\,\)、第\(\,4\,\)となります。

ただし、軸はどの象限にも含まれません。

\(\color{red}{\fbox{　平面での分点の公式　}}\)

　平面上の\(\,2\,\)点\(\,\mathrm{A}(\,x_1\,,\,y_1\,)\,,\,\mathrm{B}(\,x_2\,,\,y_2\,)\,\)に対し、
　線分\(\,\mathrm{AB}\,\)を\(\,m:n\,\)に内分する点を\(\,\mathrm{P}(\,x\,,\,y\,)\,\)とすると
　\(\hspace{10pt}\displaystyle \color{red}{x=\frac{n\,x_1+m\,x_2}{m+n}\,,\,y=\frac{n\,y_1+m\,y_2}{m+n}}\)

これはそれぞれの軸に垂線を下ろせば数直線の場合と同じように見ることができます。
数直線で内分点、外分点を見たときと同じように、\(\,x\,\)座標、\(\,y\,\)座標別々にみれば良いということです。

中点についても同じことが言えます。

\(\color{red}{\fbox{　中点の座標　}}\)

　平面上の\(\,2\,\)点\(\,\mathrm{A}(\,x_1\,,\,y_1\,)\,,\,\mathrm{B}(\,x_2\,,\,y_2\,)\,\)の中点は
　\(\hspace{10pt}\displaystyle \color{red}{\left(\frac{x_1+x_2}{2}\,,\,\frac{y_1+y_2}{2}\right)}\)

もちろん、中点とは\(\,1：1\,\)に内分する点のことです。

外分点は\(m:(-n)\)に内分すると形式的に見ておけば数直線の場合と同じです。
\(\hspace{10pt}\displaystyle \color{red}{(\,x\,,\,y\,)=\left(\frac{-n\,x_1+m\,x_2}{m-n}\,_,\,\frac{-n\,y_1+m\,y_2}{m-n}\right)}\)

\(\color{red}{\fbox{　２点間の距離　}}\)

　\(\,2\,\)点\(\,\mathrm{A}(\,x_1\,,\,y_1\,)\,,\,\mathrm{B}(\,x_2\,,\,y_2\,)\,\)間の距離は
　\(\hspace{10pt}\displaystyle \color{red}{\mathrm{AB}=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}}\)
特に、
　原点\(\,\mathrm{O}\,\)と点\(\,\mathrm{P}\,(\,x\,,\,y\,)\,\)の間の距離は
　\(\hspace{10pt}\displaystyle \color{red}{\mathrm{OP}=\sqrt{x^2+y^2}}\)

この公式は「三平方の定理」による表現なので中学の頃からなじみがあるでしょう。

直線の方程式

直線は\(\,1\,\)次関数で見慣れているグラフですが、
\(\,1\,\)次関数では軸に平行な直線が表せませんので、
一般的な直線の方程式の形を示しておきます。

\(\color{red}{\fbox{　直線の方程式の一般形　}}\)

　\(\,x\,,\,y\,\)の1次方程式
　\(\hspace{10pt}\color{red}{ax+by+c=0　･･･①}\)
　は直線を表す。
　（ただし、\(\,a=b=0\,\)ではない。）

※
\(\,\color{red}{①}\,\)は、
\(\,a≠0\,,\,b≠0\,\)のときは\(\,1\,\)次関数に変形できるので直線だとすぐに分かります。
\(\,a≠0\,,\,b=0\,\)のときは\(\hspace{10pt}\displaystyle x=-\frac{c}{a}\,\)になるので\(\,y\,\)軸に平行な直線です。
\(\,a=0\,,\,b≠0\,\)のときは\(\hspace{10pt}\displaystyle y=-\frac{c}{b}\,\)になるので\(\,x\,\)軸に平行な直線です。
ただ、
　\(\hspace{10pt}a=b=0\,\)（\(\,a=0\,\)かつ\(\,b=0\,\)）のときは特別なのです。
\(\,c≠0\,\)のときは\(\,\color{red}{①}\,\)を満たす点は1つもありませんので\(\,\color{red}{①}\,\)を表す図形は空集合です。
\(\,c=0\,\)のときはすべての点が\(\,\color{red}{①}\,\)を満たすので\(\,\color{red}{①}\,\)は平面全体を表します。

しかし、あまり深く考えなくて良いです。笑
（場合分けをする必要がある問題なら考えるべきことですが、教科書には書いてありません。）

\(\color{red}{\fbox{　直線の方程式その2　}}\)

　点\(\,\mathrm{P_0}\,(\,x_0\,,\,y_0\,)\,\)を通り、傾きが\(\,m\,\)である直線の方程式は
　\(\hspace{10pt}\color{red}{y-y_0=m\,(\,x-x_0\,)}\)
　である。

この形は大切なので必ず覚えておきましょう。
というのも傾きはいろいろな方法で出すことができますので、
この形さえ覚えておけば次の方程式なども覚える必要はなくなるのです。

\(\color{red}{\fbox{　直線の方程式その3　}}\)

　相違なる\(\,2\,\)点\(\,\mathrm{P_1}\,(\,x_1\,,\,y_1\,)\,,\,\mathrm{P_2}\,(\,x_2\,,\,y_2\,)\,\)を通る直線の方程式は、
　(1)　\(\,x_1≠x_2\,\)　なら　\(\displaystyle \,y-y_1=\frac{y_2-y_1}{x_2-x_1}\,(\,x-x_1\,)\,\)
　(2)　\(\,x_1=x_2\,\)　なら　\(\,x=x_1\,\)
で与えられる。
※
(2)は分母が\(\,0\,\)になることはないので別に考える必要が出てきますが、
\(\,x\,\)座標が同じで\(\,2\,\)点を通るならy軸に平行だと分かります。

傾きは変化の割合なので、
　\(\displaystyle (傾き)=\frac{　(\,y\,の増加量\,)　}{　(\,x\,の増加量\,)　}\)
で別途求めれば「その2」の方程式が使えます。
その際の通る\(\,1\,\)点は\(\,\mathrm{P_1\,,\,P_2}\,\)のどちらでも良いですよ。
中学生が\(\,1\,\)次関数を求めるのと同じです。

\(\color{red}{\fbox{　直線の方程式その4　}}\)

　\(\,x\,\)軸と点\(\,(\,a\,,\,0\,)\,\)、\(\,y\,\)軸と点\(\,(\,0\,,\,b\,)\,\)
で交わる直線の方程式は
　\(\hspace{10pt}\displaystyle \color{red}{\frac{x}{a}+\frac{y}{b}=1}\)
で与えられる。
　ただし、\(\,ab≠0\,\)である。

これは\(\,x\,\)切片、\(\,y\,\)切片が分かっているときの直線の方程式です。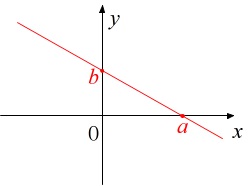
\(\,ab≠0\,\)であることは分母にある定数なので分かるでしょう。
　「\(\,a≠0\,\)　かつ　\(\,b≠0\,\)」　です。

２直線の関係

２直線の位置関係で特に取り上げて扱うのは「平行」、「一致」、「垂直」です。

\(\color{red}{\fbox{　２直線の平行条件　}}\)

　(1)\(\,2\,\)直線　\(\,y=mx+n\,,\,y=m’x+n’\,\)　が平行
　　⇔　\(\,m=m’\,\)
　(2)\(\,a’≠0\,,\,b’≠0\,\)とするとき、
　\(\,2\,\)直線　\(\,ax+by+c=0\,,\,a’x+b’y+c’=0\,\)　が平行
　　⇔　\(\displaystyle \frac{a}{a’}=\frac{b}{b’}\)　

(2)は(1)を変形すれば出てくる関係式です。

大ざっぱに言うと\(\,2\,\)直線があって、
傾きも切片も同じとき「一致する」といいます。
（\(\,2\,\)直線が重なるとき、といった方が分かり易いですね。）

一般的にまとめると

\(\color{red}{\fbox{　２直線の一致条件　}}\)

　(1)　\(\,2\,\)直線　\(\,y=mx+n\,,\,y=m’x+n’\,\)　が一致する。
　　⇔　\(\,m=m’\,\)　かつ　\(\,n=n’\,\)
　(2)　\(\,2\,\)直線　\(\,ax+by+c=0\,,\,a’x+b’y+c’=0\,\)　が一致する。
　　⇔　\(\,k≠0\,\)　として　\(\,a=ka’\,,\,b=kb’\,,\,c=kc’\,\)　を満たす。
　　（各係数が比例すること。）

(2)が言いたいのは、
　\(\,x+2y=3\,\)　と　\(\,2x+4y=6\,\)
は同じ直線を表しているということです。

次は垂直条件です。

\(\color{red}{\fbox{　２直線の垂直条件　}}\)

　(1)　\(\,2\,\)直線　\(\,y=mx+n\,,\,y=m’x+n’\,\)　が直交する。
　　⇔　\(\,m\,n=-1\,\)
　(2)　\(\,2\,\)直線　\(\,ax+by+c=0\,,\,a’x+b’y+c’=0\,\)　が直交する。
　　⇔　\(\,aa’+bb’=0\,\)

(2)は直線が軸に平行な場合も使える幅広い条件です。
※
ベクトルを学んだ後なら、方向ベクトルや法線ベクトルの垂直条件で内積が\(\,0\,\)なので分かり易くなります。

「\(\,2\,\)直線の垂直条件」からよくある垂線の方程式があります。

\(\color{red}{\fbox{　垂線の方程式　}}\)

　(1)　\(\,y=mx+n\,\)　に垂直な直線は
　　\(\,m≠0\,\)　のときは　\(\displaystyle y=-\frac{1}{m}\,x+n’\)
　で表される。
　(2)　\(\,ax+by+c=0\,\)　に垂直な直線は
　　\(\hspace{10pt}bx-ay+c’=0\)　で表される。

傾きは垂直条件から見れば明らかです。
定数項は通る点によって変わりますので気をつけましょう。

⇒　ある点を通る直線の条件がもう一つの直線と垂直のときの方程式の求め方

式の形を覚えるよりは、分かる限りの情報を座標上に示すことがポイントになります。

⇒　直線に対して対称な点の座標の求め方

中点であることと垂直条件を使います。

\(\color{red}{\fbox{　点と直線との距離の公式　}}\)

　点\(\,\mathrm{P}\,(\,x_0\,,\,y_0\,)\,\)から
　直線　\(\,ax+by+c=0\,\)　に下ろした垂線の長さを\(\,d\,\)とすれば
　　\(\hspace{10pt}\displaystyle \color{red}{d=\frac{|\,a\,x_0+b\,y_0+c\,|}{\sqrt{\,a^2+b^2\,}}}\)
　である。

点\(\,\mathrm{P}\,\)を原点とすると
　　\(\hspace{10pt}\displaystyle \color{blue}{d=\frac{|\,c\,|}{\sqrt{\,a^2+b^2\,}}}\)
となりますが、別に覚える必要はありません。
上の公式で　\(\,x_0=y_0=0\,\)　を代入すればすぐに出てくる公式です。

円

円の定義は、
　「定点からの距離が一定である点の集合」
です。

ここでは円を方程式で表し、座標上での位置関係などを見ておきます。

注意：
ここは要点ページなのに少し長くなってきたので（余計なことを書いてる？）、
ここから先は簡単にまとめていきます。

円の方程式

\(\color{red}{\fbox{　円の方程式　}}\)

　点\(\,\mathrm{C}\,(\,a\,,\,b\,)\,\)を中心とし、半径が\(\,r\,\)の円の方程式は
　　\(\hspace{10pt}\color{red}{(\,x-a\,)^2+(\,y-b\,)^2=\,r^2}\)
　特に、原点を中心とする円は
　　\(\hspace{10pt}\color{red}{\,x\,^2+\,y\,^2=\,r^2}\)

半径\(\,r\,\)については必ず\(\,r＞0\,\)です。

円の方程式を展開することによって、円の方程式の一般形が得られます。

\(\color{red}{\fbox{　円の方程式の一般形　}}\)

　　一般に、円は\(\,x^2\,\)と\(\,y^2\,\)の係数が等しく、
　\(\,xy\,\)の項を含まない\(\,x,y\,\)についての\(\,2\,\)次方程式
　\(\hspace{10pt}\color{red}{x^2+y^2+Ax+By+C=0}\)
　で表される。

\(\,\mathrm{A,B,C}\,\)は定数です。

⇒　「３点を通る円」と「２点とある直線上に中心がある円」の方程式の求め方

円は中心と半径が分かれば方程式が決まります。
式で処理する場合、\(3\)点を通る問題が一番計算がややこしくなりますよね。笑

円と直線

円と直線の位置関係と接線についてのまとめです。

\(\color{red}{\fbox{　円と直線の位置関係と共有点　}}\)

　半径\(\,r\,\)の円\(\,\mathrm{C}\,\)と直線\(\,\ell\,\)において
　\(\,\mathrm{C}\,\)の中心と\(\,\ell\,\)との距離\(\,d\,\)が
　(1)　\(\,d＜r\,\)　のとき異なる\(\,2\,\)点で交わる。
　(2)　\(\,d=r\,\)　のとき接する。
　(3)　\(\,d＞r\,\)　のとき共有点を持たない。
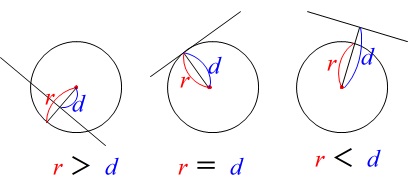図で見れば明らかです。

式による解析をしておくと、
円\(\,\mathrm{C}\,\)と直線\(\,\ell\,\)を連立すると２次方程式になるので、
その判別式\(\,D\,\)で円と直線の関係を見ることができます。

　(1′)　\(\,D＞0\,\)　のとき
　連立した\(\,2\,\)次方程式は異なる2つの実数解を持ち、\(\,2\,\)点で交わる。
　(2′)　\(\,D=0\,\)　のとき
　連立した\(\,2\,\)次方程式は重解を持ち、接する。
　(3′)　\(\,D＜0\,\)　のとき
　連立した\(\,2\,\)次方程式は実数解を持たず、交点を持たない。

とも言えます。

「共有点の個数」と聞かれた場合は、
　\(\,2\,\)個、\(\,1\,\)個、\(\,0\,\)個
と個数で答えましょう。

次は円の接線についてです。
円と直線の位置関係において\(\,r=d\,\)の場合ですね。

\(\color{red}{\fbox{　円の接線の性質　}}\)

　(1)　円の接線は接点を通る半径に垂直である。
　(2)　円と直線が与えられたとき直線が円の接線である。
　　⇔　円の中心から直線までの距離が円の半径に等しい。
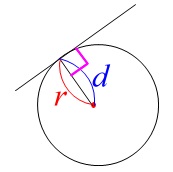(2)は点と直線の距離の公式を利用する問題でよく使う事実です。

\(\color{red}{\fbox{　円の接線の公式　}}\)

　円　\(\,x^2+y^2=r^2\,　(\,r\,＞\,0\,)\)　の上の点、
　\(\,\mathrm{P}\,\color{red}{(\,\,x_0\,,\,y_0\,)}\,\)における接線の方程式は
　　\(\hspace{10pt}\color{red}{x_0\,x+y_0\,y=r^2}\)

これは原点中心の円の場合です。

\(\color{red}{\fbox{　中心が原点ではない円も含め一般的な接線の公式　}}\)

　円　\(\,(x-a)^2+(y-b)^2=r^2\,\)　の上の点、
　\(\,\color{red}{\mathrm{P}\,(\,\,x_0\,,\,y_0\,)}\,\)における接線の方程式は
　　\(\hspace{10pt}\,\color{red}{(x_0-a)(x-a)+(y_0-b)(y-b)=r^2}\,\)

一般的な形で覚えておけば原点中心は必要ないですが、
原点中心の場合の接線は単位円を扱うときは便利なので使い分けると良いです。

⇒　円に接する直線（接線の方程式）の求め方３パターン

円というと図形（幾何）というイメージかもしれませんが、
円を扱う分野は多いので練習を多めにしておくべきです。

２つの円

\(\,2\,\)円の相互の位置関係です。
５つの場合がありますが、２円の半径と中心間の距離で見分けることができます。

\(\color{red}{\fbox{　２つの円の位置関係　}}\)

　\(\,2\,\)円の半径を　\(\,r\,,\,r’\,(\,r\,＞\,r’\,)\)、中心間の距離を\(\,d\,\)とすると
　(1)　\(\,d\,＞\,r+r’\,\)　⇔　互いに他の外部にある。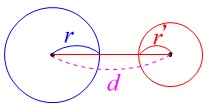
　(2)　\(\,d=r+r’\,\)　⇔　外接する。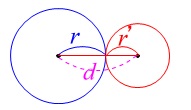
　(3)　\(\,r-r’\,＜\,d\,＜r+r’\,\)　⇔　\(\,2\,\)点で交わる。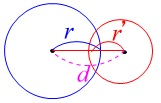
　(4)　\(\,d=r-r’\,\)　⇔　内接する。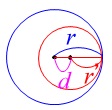
　(5)　\(\,d\,＜\,r-r’\,\)　⇔　一方が他方の内部にある。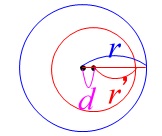

2つの円を連立して解を調べることもできますが、計算がややこしくなることが多いです。

2つの円の交点を通る曲線

曲線の交点を通る曲線群について一般的に考察すると難しくなるので、
2つの円が交点を持つ場合についてまとめておきます。

\(\color{red}{\fbox{　２つの円の交点を通る円または直線　}}\)

　２つの円
　\( \begin{cases}
\hspace{7pt} x^2+y^2+ax+by+c=0　･･･①\\ \\
\hspace{7pt} x^2+y^2+a’x+b’y+c’=0　･･･②
\end{cases}\)
が交わるとき、方程式
　\(\color{red}{x^2+y^2+ax+by+c+k( x^2+y^2+a’x+b’y+c’)=0　･･･③}\)
は、\(\,k\,\)の値によらず２つの円①②の交点を通る円または直線を表す。

③において\(\,k=-1\,\)のとき\(\,x^2\,,\,y^2\,\)の項が消えて
　\(\hspace{10pt}\color{blue}{(a-a’)x+(b-b’)y+(c-c’)=0}\)
で表される直線になります。

このとき2つの場合があります。
　(1)　2つの円が交わる場合は、２交点を結ぶ直線になります。
これを「共通弦」と言います。
　(2)　2つの円が接する場合は、2つの円の「接点における共通接線」になります。

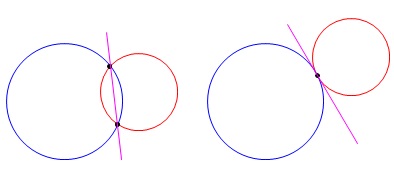
2つの円が交わることが前提です。

※
共通接線は2つの円が交わらないときにも存在しますが、接点損ものがないので「接点おける共通接線」は存在しません。

要点だけで簡単に、短くしたいのに、長くなってますね。
（この時点で読んでいる人はまだいるのだろうか？と疑問が出てきた。笑）

軌跡と領域

平面上の点\(\,\mathrm{P}\,\)に対し、ある条件を満たす点\(\,\mathrm{P}\,\)全体が描く図形を軌跡と言います。

軌跡と方程式

軌跡の方程式を求めるとき気をつけなければならないことがありますが、
手順は簡単なので確認しておきます。

\(\color{red}{\fbox{　軌跡の方程式　}}\)

　軌跡の方程式は\(\,\mathrm{P}(x\,,\,y)\,\)が軌跡上の点であるための、\(\,x\,,\,y\,\)の必要十分条件。

難しく見えますが手順を確認すれば必要十分になります。

\(\color{blue}{\fbox{　軌跡の方程式を求める手順　}}\)

　(1)　点\(\,\mathrm{P}(x\,,\,y)\,\)に関する条件を方程式で表し、その方程式が表す図形を調べる。（必要性）
　(2)　求めた方程式が表す図形が、点\(\,\mathrm{P}\,\)の条件を満たすことを確かめる。（十分性）

普通の問題であれば必要十分なまま方程式が表せますので深く考えなくても良いですが、
制限がつく軌跡もあるので、少しだけ気をつけておきましょう。

⇒　軌跡の求め方（放物線の頂点や内分点の軌跡）

普通の軌跡問題の手順解説です。

不等式の表す領域

不等式で表す領域は、上か下か、内部か外部か、を見分けられればいいです。

\(\color{red}{\fbox{　直線と領域　}}\)

　直線\(\,\ell\,\)を\(\,y=mx+n\,\)とすると、
　(1)　不等式　\(\,y\,＞\,m\,x+n\,\)　の表す領域は、
　　直線\(\,\ell\,\)の上側で境界は含まない。
　(2)　不等式　\(\,y\,＜\,m\,x+n\,\)　の表す領域は、
　　直線\(\,\ell\,\)の下側で境界は含まない。

※
境界は直線上の点の集合のことになります。

不等式が\(\,y\,≧\,m\,x+n\,,\,y\,≦\,m\,x+n\)のように、
等号を持つときは境界を含みます。

\(\color{red}{\fbox{　円と領域　}}\)

　円\(\,\mathrm{C}\,\)を\(\,x^2+y^2=r^2\,\)とすると、
　(1)　不等式　\(\,x^2+y^2\,＜\,r^2\,\)　の表す領域は、
　　円\(\,\mathrm{C}\,\)の内部。（境界含まず。）
　(2)　不等式　\(\,x^2+y^2\,＞\,r^2\,\)　の表す領域は、
　　円\(\,\mathrm{C}\,\)の外部。（境界含まず。）

境界になる円周上の点の扱いは直線の場合と同じです。

\(\color{red}{\fbox{　連立不等式の表す領域　}}\)

　連立不等式の表す領域は、それぞれの不等式の表す領域の共通部分。

連立不等式の表す領域ついては、
一つひとつの領域の『交わる』部分を示せば良いだけです。

⇒　領域：連立不等式の範囲を図示する方法と格子点と面積の求め方

格子点まで含めた問題で解説しています。

⇒　円の中心や半径が示す領域（存在範囲）を座標上に図示する方法

ちょっとした領域の応用問題です。