円の中心や半径が文字を含んでいて変化するとき、存在できる範囲は変わります。
その領域を座標上に図示する問題がありますが、ちょっと分かりづらい問題が多いです。
文字の処理と座標に慣れておくことが大切なのですが、その前に問題の意味を理解することから始めましょう。
領域問題の難点
意味のとりにくい領域問題は難関大学の入試でもよく出てくるのですが、
条件を式にして進めるか、図を書いて探りを入れていくか、になります。
できる限り図を書いてイメージする方が良いのですが、
図示しにくい問題もあるので条件式との両方から見ていく、というのが解答の道筋は見えやすくなりますよ。
いずれにしても得点に差の出る問題になることが多いです。
実数 \( t\) に対し、
方程式 \( (x-2t)^2+y^2=(5-t)^2\) で表される
\( xy\) 平面上の図形を \( C_t\) とする。
\(t\) が変化するとき \( C_t\) の通りうる範囲を \( xy\) 平面上に図示せよ。
おそらく、パッと見た目何を聞いているのか分からなかったのではないでしょうか?
\( C_t\) は
\( (x-2t)^2+y^2=(5-t)^2\) ・・・①
で表される円です。
\( t\) が変化するとどうなる?
\( xy\) 平面上に図示する?何を?
「何だか訳が分からん」
って感じじゃないですか。
解法には判別式を使ってみますが、その前にちょっと具体的に図形を見ておきたいと思いませんか?
与えられた円がどういう動きをするのか見ておくことができれば少しは答のイメージができるでしょう。
軌跡や領域は点の集まり
実数 \( t\) をいろいろ換えて代入して見ましょう。
その1つひとつを図示していくと見えてくるかもしれませんからね。
「やってみればわかる」ではなく、「やってみないとわからない」なんですよ。
この地道な作業は大きな差になります。
例えば、
\( (x-2t)^2+y^2=(5-t)^2\) ・・・①
に中心や半径がきれいな数値になる \( t\) をいくつか入れて見ます。
\( t=0\) のとき \( x^2+y^2\,=\,5^2\)
これは 中心 \( (0\,,\,0)\) 半径5の円。
\( t=1\) のとき \( (x-2)^2+y^2\,=\,4^2\)
これは 中心 \( (2\,,\,0)\) 半径4の円。
\( t=2\) のとき \( (x-4)^2+y^2\,=\,3^2\)
これは 中心 \( (4\,,\,0)\) 半径3の円。
\( t=3\) のとき \( (x-6)^2+y^2\,=\,2^2\)
これは 中心 \( (6\,,\,0)\) 半径2の円。
\( t=4\) のとき \( (x-8)^2+y^2\,=\,1^2\)
これは 中心 \( (8\,,\,0)\) 半径1の円。
\( t=5\) のとき \( (x-10)^2+y^2\,=0\)
これは、点 \( (10\,,\,0)\) です。
\( t=6\) のとき \( (x-12)^2+y^2\,=1^2\)
これは 中心 \( (12\,,\,0)\) 半径1の円。
\( t=7\) のとき \( (x-14)^2+y^2\,=2^2\)
これは 中心 \( (14\,,\,0)\) 半径2の円。
と続けて行くと見えてきました。
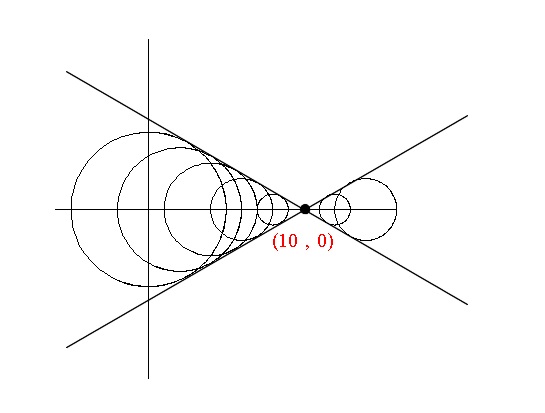
だいたいですが、2直線の左右になりそうです。
これは、あなたがやることですよ。
他人は試験中やって見せてはくれませんからね。
これを論理的に示します。
直感から論理へ
変化するのは \( t\) です。
このようなときは、\(xy\) の関数とみるのではなく、
「実数 \( t\) 」に着目し、
\( (x-2t)^2+y^2=(5-t)^2\)
を \( t\) の2次関数と見てみると良いです。
つまり、\( x\,,\,y\) を定数とみなす、ということですね。
すると、
「 \( (x-2t)^2+y^2=(5-t)^2\) を満たす実数 \( \color{red}{t}\) が存在する。」
が条件となります。
実数 \( t\) の2次方程式として整理すると①は、
\( 3t^2+2(5-2x)t+x^2+y^2-25=0\) ・・・①’
この判別式は、
\( D/4=(5-2x)^2-3(x^2+y^2-25)\\ \\
=25-20x+4x^2-3x^2-3y^2+75\\ \\
=x^2-20x-3y^2+100\)
①’が実数解を \( t\) 持つためには、
\( D≧ 0\) であればいいので、
\( D/4=x^2-20x-3y^2+100\\ \\
=x^2-20x-(3y^2-100)\\ \\
=x^2-20x-(\sqrt{3}y+10)(\sqrt{3}y-10)\\ \\
=\{x-(\sqrt{3}y+10)\}\{x+(\sqrt{3}y-10)\}\)
よって
\( (x-\sqrt{3}-10)(x+\sqrt{3}y-10)≧ 0\) ・・・②
が成り立てばよいということになります。
「 \( ab≧ 0\) 」となるのは
「 \( a≧ 0\) かつ \( b≧ 0\) 」または 「 \( a≦ 0\) かつ \( b≦ 0\) 」
(「両方0以上」か「両方0以下」のとき「積は0以上」となります。)
の2つの場合があるので、
②は、
「 \( x-\sqrt{3}y-10≧ 0\) かつ \( x+\sqrt{3}y-10≧ 0\) 」 ・・・③
または
「 \( x-\sqrt{3}y-10≦ 0\) かつ \( x+\sqrt{3}y-10≦ 0\) 」 ・・・④
この領域を図示すれば、おしまいです。
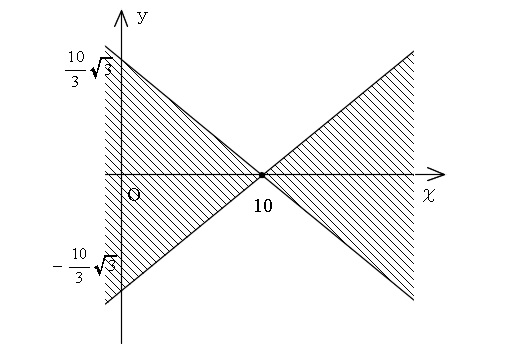
直線の上下は分かりますよね。
\( \color{red}{y≧ax+b}\) のときは \( y=ax+b\) の上(以上)です。
\( \color{red}{y≦ ax+b}\) のときは \( y=ax+b\) の下(以下)です。
②への変形のときのタスキガケを思いつくかどうかは大きなポイントになりますが、
おおよその図形から直線2本の間というのがわかっているので何とかなるでしょう。
「 \( t\) の2次方程式として \( t\) の実数解条件」
への考え方の転換、良いですね?
こちらもグラフがカギでした。
全体的な基本用語から確認しておきましょう。