円を表す領域に対し、直線の切片の最大値、最小値を求める問題がありますが、その解き方と考え方です。
考え方はいろいろとありますが、判別式を利用することが多いので計算処理の力も必要になります。
基本的なレベルでは2次関数、2次方程式との融合になりますので判別式とともに復習しておくと良いです。
領域と存在範囲
領域そのものがイメージしにくいところなので、例題を見ながらの方が良いですね。
イメージし易くなる方法をお伝えします。
点 \( (x\,,\,y)\) が2つの不等式 \( x^2+y^2≦4\,,\,x≦ 0\) を同時にみたすとき、
\( x-\sqrt{3}y\) の存在範囲を求めよ。
このような領域と最大最小などの範囲を聞かれたとき、式だけで処理しようとするとたいへんな計算が待っています。
もちろんその処理能力を問われている場合もありますが、
グラフを利用すると楽になることが多いですよ。
「 \( x-\sqrt{3}y\) の存在範囲」
のように単なる文字式で、値の見当もつかない場合は、
\( x-\sqrt{3}y=\color{red}{k}\) ・・・①
とおき、グラフで \( \color{red}{k}\) の値の変化を見ていくのがわかりやすいです。
領域は図やグラフで確認する
「2つの不等式 \( x^2+6y^2≦ 4\,,\,x≦ 0\) 」
とは、原点中心で半径が2の円の左半分です。
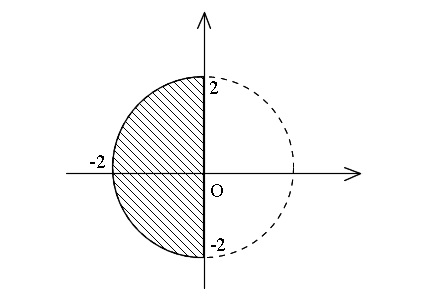
これと、直線 \(x-\sqrt{3}y=k\) の交点のある範囲を見ていくのです。
\( x-\sqrt{3}y=k\\ \\
\hspace{5pt} \Leftrightarrow \hspace{5pt} y=\displaystyle \frac{1}{\sqrt{3}}x-\displaystyle \frac{k}{\sqrt{3}}\)
の傾きは正で、直線は右上がりとなります。
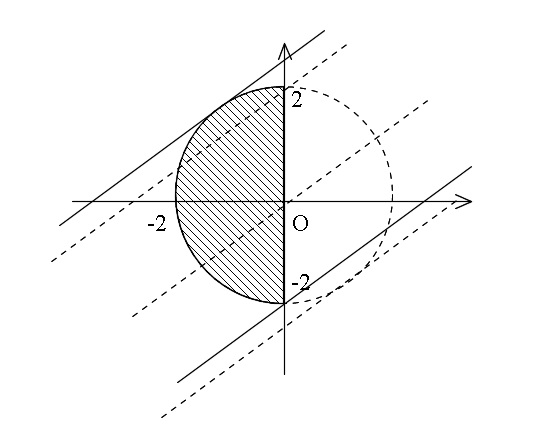
交わる範囲を見ていくと、\( x\,,\,y\) は図の斜線部分内の点なので
切片の大小を見れば良いことが分かりますが注意するのは、
切片に「-」がついているので \(\color{red}{k}\) が小さいほど切片は大きくなるということ。
切片が最小になるのは、\( (0\,,\,-2)\) を通るときです。
① の \( x-\sqrt{3}y=k\) より、
\( k=2\sqrt{3}\)
これは \(k\) の最大値となります。
切片が \(\displaystyle -\frac{k}{\sqrt{3}}\) だから
\( \color{red}{k}\) の値が大きいほど切片は小さくなります。
次に①の切片が最大になるのは、図を見てみると分かりますが
\( (0\,,\,2)\) を通るときではなく、
\( x^2+y^2=4\) に接するときです。
このときの \( k\) の値を求めるのに接点は求まりますが必要ありません。
(求めても良いですよ。)
接するので重解条件を使いましょう。
判別式の利用
\( x^2+y^2=4\) と \( x-\sqrt{3}y=k\) が接するとき、
重解条件から判別式 \( D=0\) を解いて求めることが出来るのですが、
\(y\) を消去するより \( x\) を消去した方が早いですよ。
実数となるのは \(x,y\) どちらも同じです。
\( \begin{cases}
\hspace{7pt} x^2+y^2=4\\
\hspace{7pt} x-\sqrt{3}y=k
\end{cases}
\hspace{5pt} \Leftrightarrow \hspace{5pt}
\begin{cases}
\hspace{7pt} x^2+y^2=4\\
\hspace{7pt} x=k+\sqrt{3}y
\end{cases}
\)
第2式を第1式に代入すると
\( (k+\sqrt{3}y)^2+y^2=4\\ \\
\hspace{5pt} \Leftrightarrow \hspace{5pt} k^2+2\sqrt{3}ky+3y^2+y^2=4\\ \\
\hspace{5pt} \Leftrightarrow \hspace{5pt} 4y^2+2\sqrt{3}y+k^2-4=0\)
このとき、
\( D/4=(\sqrt{3}k)^2-4(4k^2-4)\\ \\
=3k^2-4k^2+16\\ \\
=16-k^2=0\)
から \( k=\pm 4\) となりますが、
\( x≦ 0\) より、\( k=-4\) の方です。
\( k=4\) は、円の右下で接するときで、
連立不等式の領域と①との交わりがないので不適です。
(グラフの一番下の直線のときを示しています。)
\(k\) が小さいほど切片は大きくなるので、
\(k=-4\) の方だとすぐに分かりますが、注意が必要ですね。
\( x≦ 0\) という条件がなければ、\( k=4\) のとき切片が最小で良いのですが、少しひねってあります。
以上より、\( -4≦ k≦ 2\sqrt{3}\) となり、
\( \underline{-4≦ x-\sqrt{3}y ≦ 2\sqrt{3}}\)
点と直線の距離の公式の利用
ところで、重解条件(判別式)から切片の最大値を出しましたが、
「接するとき」⇔「中心からの距離が半径に等しい」
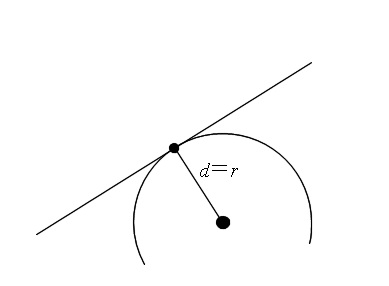
なので、「点と直線の距離の公式」が使えます。
「直線 \( x-\sqrt{3}y-k=0\) と円の中心 \( (0\,,\,0)\) の距離が半径2に等しいときに接する。」
という条件を使っても、\(k=\pm 4\) は出てきます。確認してみて下さい。
円と直線の位置関係をつかむには「点と直線の距離の公式」は応用範囲が広いですよ。
円と接線はセットで考えると良いですね。
⇒ 円の中心や半径が示す領域(存在範囲)を座標上に図示する方法
円の領域問題を解けるかどうかは、図示できるかどうかが大きな分かれ目になります。
図形と方程式は考えにくい分野ですが、扱う関数は基本的に直線、円、放物線だけです。
覚えることは少ないので要点を押さえておきましょう。