弧度法（ラジアン）の定義と三角関数の基本計算問題

三角関数は三角比を関数として扱うものですが値の出し方や三角方程式の解き方は基本的には同じです。
度分法が弧度法（ラジアン）に変わることと、範囲が広くなるだけなので先ずは定義と象限ごとの値を見ておきます。
グラフや加法定理は別に説明しますので、簡単な計算問題で三角比の復習をかねて弧度法の確認をしておきましょう。

三角比と三角関数の違い

象限の拡張

第１象限、第２象限については、「三角比」単元で値を求めることはできるようになっているでしょう。
三角関数では第３象限、第４象限まで拡張されます。

一般角で見るようになりますが、何度も繰り返されるだけなので第４象限までの値がわかれば問題はありません。
　\(\theta\)　が第１象限から第４象限まで変化するとき

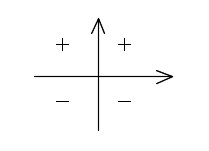
　\( \sin\theta\)　は

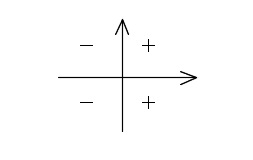
　\( \cos\theta\)　は

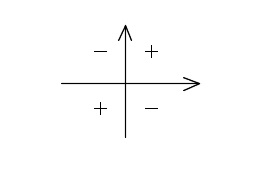
　\( \tan\theta\)　は

となります。
軸上では値が０か１か存在しないかですが、これは三角比と同じです。

⇒　三角比の公式と計算問題の解き方

ますはこの符号を覚えておきましょう。
そうすれば第１象限の値さえ出せればすべて求められるようになります。

ちなみに軸は象限には含みませんので注意してください。

度分法と弧度法

三角比と三角関数で違うのは　\(\theta\)　の表し方ですね。

三角比では　\( 30^\circ\)　などの度分法を使っていましたが、
三角関数では　\( \pi\)　などの弧度法（単位：ラジアン）を使います。

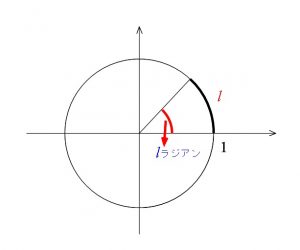
ラジアンの定義

弧度法の定義をしておきます。

これによると、半径１の円である単位円において、
　弧の長さ　\( \ell\)　の円弧を見込む中心角の大きさを弧度法で表すと　\(\ell\)　ラジアンになります。

度分法と弧度法を並べて見ると、
　
　\(\displaystyle \color{red}{360^\circ=2\pi}\,,\,\color{red}{180^\circ=\pi}\,,\,\color{red}{90^\circ=\frac{\pi}{2}}\)

となります。
大きさは比例関係になるので　\( \color{red}{360^\circ=2\pi}\)　さえ覚えていれば度分法から弧度法への変換は何とかなります。

三角関数は関数なので当然グラフを意識するのですが、グラフの書き方や加法定理などの定理は別にやりますので、復習をかねて計算問題をやっておきましょう。

式の値を求める基本問題

（１）条件式だけでは　\( \sin\theta\,,\,\cos\theta\)　は具体的に求まりません。
三角比や対称式でやったように、与式を２乗しましょう。

　\( (\sin\theta-\cos\theta)^2\\ \\
=\sin^2\theta-2\sin\theta\cos\theta+\cos^2\theta\\ \\
=\sin^2\theta+\cos^2\theta-2\sin\theta\cos\theta\)

ここで　\( \sin^2\theta+\cos^2\theta=1\)　は三角比のときと同じように成り立つので

　\( (\sin\theta-\cos\theta)^2\\ \\
=1-2\sin\theta\cos\theta\\ \\
=1-2\times \left(-\displaystyle \frac{1}{4}\right)=\displaystyle \frac{3}{2}\)

これは与式の２乗なので平方根をとりますが
　\( \theta\)　が第２象限の角なので

　\( \sin\theta>0\,,\,\cos\theta\,<\, 0\)

であることから、与式は正の値をとることがわかります。

　\( \sin\theta-\cos\theta =\displaystyle \frac{\sqrt{3}}{\sqrt{2}}=\underline{\displaystyle \frac{\sqrt{6}}{2}}\)

（２）も同様な問題で既に練習はしているはずですが確認です。
与式を変形するのですが対称式（交代式）変形か、因数分解変形かで違ってきます。
大した差はありませんが、三角比、三角関数では因数分解変形が若干楽になります。

因数分解すると

　\( \sin^3\theta-\cos^3\theta\\ \\
=(\sin\theta-\cos\theta)(\sin^2\theta+\sin\theta\cos\theta+\cos^2\theta)\\ \\
=\displaystyle \frac{\sqrt{6}}{2}\left(1-\displaystyle \frac{1}{4}\right)\\ \\
=\displaystyle \frac{\sqrt{6}}{2}\times \displaystyle \frac{3}{4}=\underline{\displaystyle \frac{3\sqrt{6}}{8}}\)

（１）で　\(\displaystyle \sin\theta-\cos\theta=\frac{\sqrt{6}}{2}\)　は求めていることは忘れないでください。

対称式（交代式）変形すると

　\( \sin^3\theta-\cos^3\theta\\ \\
=(\sin\theta-\cos\theta)^3+3\sin\theta\cos\theta(\sin\theta-\cos\theta)\\ \\
=\left(\displaystyle \frac{\sqrt{6}}{2}\right)^3+3\times\left(-\displaystyle \frac{1}{4}\right)\times \displaystyle \frac{\sqrt{6}}{2}\\ \\
=\displaystyle \frac{6\sqrt{6}}{8}-\displaystyle \frac{3\sqrt{6}}{8}\\ \\
=\underline{\displaystyle \frac{3\sqrt{6}}{8}}\)

と、いずれにしても答えは簡単に出ますが、
　\( \sin\theta\,,\,\cos\theta\)　が絡むときは、

　\( \color{red}{\sin^2\theta+\cos^2\theta=1}\)

が利用出来るので因数分解が結果まで早い場合が多いです。

三角方程式の基本問題

「ラジアン」で与えられた場合でも第一象限であることは確認しておきましょう。

　\(\tan x>0\)　です。

まずは三角方程式を解きますが、三角比と同じで、
「　\( \sin x\,,\,\cos x\)　のどちらかに統一」
ですね。

　\( 3\cos^2x+7\sin x=5\\ \\
\hspace{5pt} \Leftrightarrow \hspace{5pt} 3(1-\sin^2 x)+7\sin x-5=0\\ \\
\hspace{5pt} \Leftrightarrow \hspace{5pt} -3\sin^2+7\sin x+2=0\\ \\
\hspace{5pt} \Leftrightarrow \hspace{5pt} 3\sin^2-7\sin x-2=0\\ \\
\hspace{5pt} \Leftrightarrow \hspace{5pt} (3\sin x-1)(\sin x-2)=0\)

ここで　\(\displaystyle 0< x < \frac{\pi}{2}\)　が効いてきます。

　\( 0< \sin x< 1　,　0< \cos x< 1\)

です。
これから　\(\sin x-2\neq 0\)　なので

　\( \sin x=\displaystyle \frac{1}{3}\)

　\( \cos^2x=1-\sin^2x\)　から

　\( \cos^2x=1-\left(\displaystyle \frac{1}{3}\right)^2=\hspace{5pt}1-\displaystyle \frac{1}{9}\hspace{5pt}=\hspace{5pt}\displaystyle \frac{8}{9}\)

　\( ∴ \hspace{7pt}\cos x=\sqrt{1-\displaystyle \frac{1}{9}}\hspace{5pt}=\hspace{5pt}\displaystyle \frac{2\sqrt{2}}{3}\)

よって、

　\( \tan x=\hspace{5pt} \displaystyle \frac{\sin x}{\cos x}\hspace{5pt}=\hspace{5pt}\displaystyle \frac{\displaystyle \frac{1}{3}}{\displaystyle \frac{2\sqrt{2}}{3}}\\ \\
=\hspace{5pt}\displaystyle \frac{1}{3}\div \displaystyle \frac{2\sqrt{2}}{3}\hspace{5pt}=\hspace{5pt}\displaystyle \frac{1}{3}\times \displaystyle \frac{3}{2\sqrt{2}}\\ \\
=\hspace{5pt}\displaystyle \frac{1}{2\sqrt{2}}\hspace{5pt}=\hspace{5pt}\underline{\displaystyle \frac{\sqrt{2}}{4}}\)

計算の途中はなくても良いですが、繁分数の処理にも慣れておきましょう。

また

　\( 1+\tan^2x=\displaystyle \frac{1}{\cos^2 x}\\ \\
\hspace{5pt} \Leftrightarrow \hspace{5pt} \tan^2x=\displaystyle \frac{1}{\cos^2x}-1\)

から
　
　\( \tan^2x=\displaystyle \frac{1}{\left(\displaystyle \frac{8}{9}\right)}-1\\ \\
=1\div \displaystyle \frac{8}{9}-1\hspace{5pt}=\hspace{5pt}1\times \displaystyle \frac{9}{8}-1\hspace{5pt}=\hspace{5pt}\displaystyle \frac{1}{8}\)

からでも同じ答は出せますし、計算に大した差は無いのでどちらでも良いです。

ここまではまだ復習です。
覚えることが難しいとされる三角関数ですが、覚えることを少なくして使えるようにすれば良いだけですよ。

三角比で学んだ知識は必要になります。
基本は復習しておきましょう。

⇒　三角関数と加法定理の要点

加法定理は覚えていなければ三角関数は捨てているのと同じです。