三角関数の2倍角、3倍角の公式を利用した三角方程式と三角方程式の解き方の説明です。
三角関数で最も重要なのは加法定理ですが、他の公式もかなりの割合で出題されますので見ておいてください。
加法定理を覚えていれば導くことができる公式ですが、試験時間に余裕の無い人は覚えておいた方が良いかもしれません。
三角方程式と不等式の扱い方
\( \sin\theta\) や \( \cos\theta\) などで成り立つ方程式・不等式を三角方程式・三角不等式といいます。
これらの解き方は今までの \( x\) に関する方程式などと同じですが、
通常 \( \theta\) について求めるので最後まで求めてください。
\( \sin\theta\) や \( \cos\theta\) などの \( \theta\) は、
途中は度分法( \(30^\circ\) など)に直して考えても良いですが、
\( \theta\) の範囲がラジアンで与えられたときは、答えもラジアンにしておきましょう。
やっかいに感じるかもしれませんが、数学ⅠAでは「度分法」、数学ⅡBでは「弧度法」で表現されるので、どちらにも慣れておいてください。
問題を見てみましょう。
\( 0≦ \theta ≦ \pi\) とする。
次の不等式を解け。
\(\displaystyle \frac{2}{3}\cos^2\theta ≧ 1-\cos\left(\frac{\pi}{2}-\theta\right)\)
三角方程式を解く場合は \( \sin\) か \( \cos\) のどちらかで統一するのが基本です。
\( \displaystyle \frac{2}{3}\cos^2\theta ≧ 1-\cos\left(\displaystyle \frac{\pi}{2}-\theta\right)\)
は \( \cos\) で統一されているように見えますが、
ラジアンの表現が違っています。
左辺は \( \theta\) ,右辺は \(\displaystyle \left(\frac{\pi}{2}-\theta\right)\) です。
三角方程式・不等式を解く時は、\( \sin\theta\) や \( \cos\theta\) も1つにしますが、
\( \theta\) にあたる角度、ラジアンの形も統一します。
ここでは、 \(\displaystyle \left(\frac{\pi}{2}-\theta\right)\) を \( \theta\) にしましょう。
三角比と同様に、
\(\displaystyle \color{red}{\sin\left(\frac{\pi}{2}-\theta\right)=\cos\theta} , \color{red}{\cos\left(\frac{\pi}{2}-\theta\right)=\sin\theta}\)
です。
さらに、変換は他にもありました。
\(\displaystyle \color{red}{\sin\left(\frac{\pi}{2}+\theta\right)=\cos\theta} , \color{red}{\cos\left(\frac{\pi}{2}+\theta\right)=-\sin\theta}\)
三角比で
\( \color{red}{\sin(\pi-\theta)=\sin\theta} , \color{red}{\cos(\pi-\theta)=\cos\theta}\)
もやっていますね。
\( \color{red}{\sin(-\theta)=-\sin\theta} , \color{red}{\cos(-\theta)=\cos\theta}\)
これも \( x\) 軸に対称なので覚えておいてください。
問題を解いて行きましょう。
\( \cos\left(\displaystyle \frac{\pi}{2}-\theta\right)=\sin\theta\)
と変換できれば与不等式は、
\( \displaystyle \frac{2}{3}\cos^2\theta ≧ 1-cos\left(\displaystyle \frac{\pi}{2}-\theta\right)\\ \\
\hspace{5pt} \Leftrightarrow \hspace{5pt} \displaystyle \frac{2}{3}\cos^2\theta ≧ 1-\sin\theta\)
となるのでこの後は \( \sin\theta\) に統一ですね。
\( \displaystyle \frac{2}{3}\cos^2\theta ≧ 1-\sin\theta\\ \\
\hspace{5pt} \Leftrightarrow \hspace{5pt} \displaystyle \frac{2}{3}(1-\sin^2\theta) ≧ 1-\sin\theta\\ \\
\hspace{5pt} \Leftrightarrow \hspace{5pt} 2(1-\sin^2\theta) ≧ 3(1-\sin\theta)\\ \\
\hspace{5pt} \Leftrightarrow \hspace{5pt} 2-2\sin^2\theta ≧ 3-3\sin\theta\\ \\
\hspace{5pt} \Leftrightarrow \hspace{5pt} -2\sin^2\theta)+3\sin\theta-1 ≧ 0\\ \\
\hspace{5pt} \Leftrightarrow \hspace{5pt} 2\sin^2\theta)-3\sin\theta+1≦ 0\)
\(\hspace{5pt} \Leftrightarrow \hspace{5pt} (2\sin\theta-1)(\sin\theta-1)≦ 0\) ・・・①
またもや不等式です。数学Ⅰの繰り返しになりますが説明しておきます。
\( ab≦ 0\) となるのは
「 \( \color{red}{a≧ 0}\) かつ \( \color{red}{b≦ 0}\) 」
または
「 \( \color{red}{a≦ 0}\) かつ \( \color{red}{b≧ 0}\) 」
の2つの場合があります。
ただ、ここでは
\( 0≦ \theta ≦ \pi\) において \( 0≦ \sin\theta ≦ 1\) なので
\( (2\sin\theta-1)(\sin\theta-1)≦ 0\) ・・・①
の1つの因数が
\( \sin\theta-1≦ 0\)
だから①は、
\( 2\sin\theta-1 ≧ 0\\ \\
\hspace{5pt} \Leftrightarrow \hspace{5pt} \sin\theta ≧ \displaystyle \frac{1}{2}\)
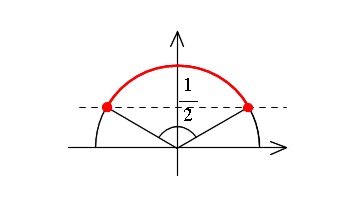
であれば良いことになります。
\( 0≦ \theta ≦ \pi\) より
\( \sin\theta ≧ \displaystyle \frac{1}{2}\hspace{5pt} \Leftrightarrow \hspace{5pt} \underline{\displaystyle \frac{\pi}{6}≦ \theta ≦ \displaystyle \frac{5\pi}{6}}\)
2倍角と3倍角の公式
問題を先に見ておきましょう。
次の方程式を解け。
\( sin x+\sin 2x+\sin 3x=0\hspace{10pt} (0< x < \pi)\)
この問題は、
2倍角公式: \( \sin 2x=2\sin x\cos x\)
3倍角の公式: \( \sin 3x=3\sin x-4\sin^3x\)
を利用する方法と、
和→積の公式:
\( \sin \color{red}{3x}+\sin \color{blue}{x}\\ \\
=\sin \displaystyle \frac{\color{red}{3x}+\color{blue}{x}}{2}\cos \displaystyle \frac{\color{red}{3x}-\color{blue}{x}}{2}\\ \\
=2\sin 2x\cos x\)
の2つが解法として選択できます。
どちらかが使えれば、三角方程式を解くことはそれほど難しくはないと思います。
これらの公式を覚えていない場合どうするか?
少し時間はかかりますが、加法定理の繰り返しで解くことが出来ます。
ただし、2倍角の公式は数学ⅡBのセンター試験などは時間との闘いとも言えますので覚えておいた方が得策ですね。
(特に数学Ⅲまで履修する場合は必須の公式となります。)
和を積に直す公式は、加法定理を書き出して加減すればすぐに出てくる公式なので覚えていなくても大丈夫です。
2倍角と3倍角の公式を導いておきます。
2倍角の公式の導き方
加法定理
\( \sin(\alpha+\beta)=\sin\alpha \cos\beta+\cos\alpha \sin\beta\)
において \( \beta=\alpha\) とおけば
\( \sin(\alpha+\alpha)\\ \\
=\sin 2\alpha\\ \\
=\sin\alpha \cos\alpha+\cos\alpha \sin\alpha\\ \\
=2\sin\alpha\cos\alpha\)
同じように
加法定理
\( \cos(\alpha+\beta)=\cos\alpha\cos\beta-\sin\alpha\sin\beta\)
において \( \beta=\alpha\) とおけば
\( \cos(\alpha+\alpha)\\ \\
=\cos\alpha\cos\alpha-\sin\alpha\sin\alpha\\ \\
=\cos^2\alpha-\sin^2\alpha\\ \\
=2\cos^2\alpha-1\\ \\
=1-\sin^2\alpha\)
この3つのどれかを使います。
3倍角の公式の導き方
加法定理の連続です。
サインの3倍角の公式は \( \sin\theta\) だけの式に直します。
\( \sin 3\theta\\ \\
=\sin(2\theta+\theta)\\ \\
=\underline{\sin 2\theta}\cos\theta+\underline{\cos 2\theta}\sin \theta\\ \\
=(\underline{2\sin\theta\cos\theta})\cos\theta+(\underline{1-2\sin^2\theta})\sin\theta\\ \\
=2\sin\theta\cos^2\theta+\sin\theta-2\sin^3\theta\\ \\
=2\sin\theta(1-\sin^2\theta)+\sin\theta-2\sin^3\theta\\ \\
=2\sin\theta-2\sin^3\theta+\sin\theta-2\sin^3\theta\\ \\
=3\sin\theta-4\sin^3\theta\)
自分で飛ばせる行があれば飛ばしてみてください。
やってみると大した計算はしていませんよ。
余弦もやっておきます。
コサインの3倍角は \( \cos\theta\) だけの式に直します。
\( \cos3\theta\\ \\
=\cos(2\theta+\theta)\\ \\
=\underline{\cos2\theta}\cos\theta-\underline{\sin2\theta}\sin\theta\\ \\
=\underline{(2\cos^2\theta-1)}\cos\theta-\underline{(2\sin\theta\cos\theta)}\sin\theta\\ \\
=2\cos^3\theta-\cos\theta-2\sin^2\theta\cos\theta\\ \\
=2\cos^3\theta-\cos\theta-2(1-\cos^2\theta)\cos\theta\\ \\
=2\cos^3\theta-\cos\theta-2\cos\theta+2\cos^3\theta\\ \\
=4\cos^3\theta-3\cos\theta\)
では問題を解きますが、和を積に換える公式は使いません。
別にやる機会があれば紹介します。
もう一度方程式を見ておくと
\( \sin x+\sin 2x+\sin 3x=0\)
2倍角、3倍角の公式を覚えていないということで進めてみます。
上の公式は、見ながら使えても意味がありませんよ。
覚えているか、導くかしないと問題用紙にはありませんからね。
同じ導くにしても一気に方程式に入れるより、
\(\sin 2x\) と \(\sin 3x\) は別に出しておきましょう。
\( \sin 2x\\ \\
=\sin(x+x)\\ \\
=2\sin x\cos x \)
サインの3倍角の公式は \( \sin x\) だけの式に直す方向で進めます。
\( \sin 3x\\ \\
=\sin(2x+x)\\ \\
=\sin 2x\cos x+\cos 2x\sin x\\ \\
=(2\sin x\cos x)\cos x+(1-2\sin^2x)\sin x\\ \\
=2\sin x\cos^2x+\sin x-2\sin^3x\\ \\
=2\sin x(1-\sin^2x)+\sin x-2\sin^3x\\ \\
=2\sin x-2\sin^3x+\sin x-2\sin^3x\\ \\
=3\sin x-4\sin^3x\)
これらを方程式にあてはめると
\( \sin x+\sin 2x+\sin 3x\\ \\
=\sin x+2\sin x\cos x+3\sin x-4\sin^3x\\ \\
=4\sin x+2\sin x\cos x-4\sin^3x\\ \\
=2\sin x(2+\cos x-2\sin^2x)\\ \\
=2\sin x\{2+\cos x-2(1-\cos^2x)\}\\ \\
=2\sin x(2+\cos x-2+2\cos^2x)\\ \\
=2\sin x(\cos x+2\cos^2x)\\ \\
=2\sin x\cos x(1+2\cos x)=0\)
このとき、
\( \sin x=0\) または \( \cos x=0\) または \( 1+2\cos x=0\)
となりますが、
\( 0< x < \pi\) の条件から \( \sin x\neq 0\) となるので
\( \sin x=0\) は不適です。
\( \cos x=0 \hspace{5pt} \Leftrightarrow \hspace{5pt} x=\displaystyle \frac{\pi}{2}\)
また
\( 1+2\cos\theta=0\hspace{5pt} \Leftrightarrow \hspace{5pt} \cos x=-\displaystyle \frac{1}{2}
\hspace{5pt} \Leftrightarrow \hspace{5pt} x=\displaystyle \frac{2\pi}{3}\)
以上のことから、
\( \sin x+\sin 2x+\sin 3x=0\)
を解くと
\( x=\underline{\displaystyle \frac{\pi}{2}\,,\,\displaystyle \frac{2\pi}{3}}\)
これだけの計算を試験中にやらなければなりません。
しかし、積を和に変える、和を積に変える公式を覚えていたとしたら?
\( \sin x+\sin 2x+\sin 3x\\ \\
=\underline{\sin x+\sin 3x}+\sin 2x\\ \\
=\underline{2\sin 2x\cos x}+\sin 2x\\ \\
=\sin 2x(2\cos x+1)=0\)
から \(\sin 2x=0\) または \(2\cos x+1=0\)
\( 0< x < \pi\) なので \( 0< 2x < 2\pi\) となることに注意して、
\( x=\underline{\displaystyle \frac{\pi}{2}\,,\,\displaystyle \frac{2\pi}{3}}\)
が求まり終わりです。
覚える時間を惜しまず公式を覚えておくか、
試験中に導けるだけの計算力をつけておくかの違いですね。
加法定理と並ぶ、三角関数もう一つの必須重要項目です。
三角関数は割と覚えることが多いです。
しかも、ややこしい関係式が出てくるので少し時間をかけて覚えるようにしましょう。
