三角関数の合成の公式の確認と合成のやり方を説明します。
合成の定理は公式になっていますが一般的なので見ても余り使えません。
そのため覚える気になれない人もいるので加法定理を覚えているという前提になりますがここで合成できるようになるまで徹底的に説明します。
三角関数の三大テーマは、
「加法定理」「合成」「グラフ」
といっても良いでしょう。
中でも加法定理と合成ができないとこの分野の得点はかなり厳しくなりますよ。
三角関数の合成の定理と証明
合成にはふた通りあります。
正弦(サイン)で合成するか、余弦(コサイン)で構成するかです。
コサインの合成は知らない人が多いかもしれませんが、
加法定理を使って導くので同じように合成できるんですよ。
余り使わない人が多いので導くだけにして、
問題を解くときはサインの合成を使うことにします。
先ずは定理(公式)を書いておきます。
具体的な導き方は後で説明しますのでここは飛ばしても良いです。
[定理]合成の公式
\( a=b=0\) ではないとき,
\( a\sin\theta+b\cos\theta=\sqrt{a^2+b^2}\sin(\theta+\alpha)\)
ただし、\( \alpha\) は点P \( (a\,,\,b)\) をとるときの動径OPが \(x\) 軸となす角。
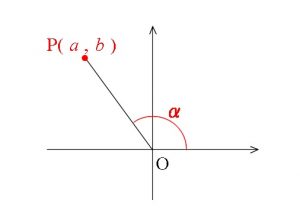
証明しておきます。
角 \( \alpha\) は \( OP=\sqrt{a^2+b^2}\) であることから
\(\displaystyle \color{red}{\cos\alpha=\frac{a}{\sqrt{a^2+b^2}}} , \color{blue}{\sin\alpha=\frac{b}{\sqrt{a^2+b^2}}}\)
を満たす。
このとき
\(\hspace{10pt} a\sin\theta+b\cos\theta\\ \\
\displaystyle=\sqrt{a^2+b^2} \left( \color{red}{\frac{a}{\sqrt{a^2+b^2}}}\sin\theta+ \color{blue}{\frac{b}{\sqrt{a^2+b^2}} }\cos\theta\right)\\ \\
=\sqrt{a^2+b^2}\hspace{5pt} (\sin\theta\color{red}{\cos\alpha}+\cos\theta\color{blue}{\sin\alpha})\\ \\
=\sqrt{a^2+b^2}\hspace{5pt} \sin(\theta+\alpha)\)
最後の2行に加法定理を使っていることを見ておいてください。
一般的には上の公式通りで良いのですが,
第1段階として具体的に \( \alpha \) が求まる場合にはどうするかを覚ええておきましょう。
正弦(サイン)の合成のやり方
例えば、
\( \sin\theta+\cos\theta\)
を合成してサインだけで表して見ます。
\( \sin\theta\) と \( \cos\theta\) の係数が両方1なので
\( \sqrt{1^2+1^2}=\sqrt{2}\)
で全体をくくって各項の係数を合わせます。
\( \sin\theta+\cos\theta\\ \\
=\underline{\sqrt{2}\left(\sin\theta\cdot\displaystyle \frac{1}{\sqrt{2}}+\cos\theta\cdot\displaystyle \frac{1}{\sqrt{2}}\right)}\)
何故この変形をしているかというと加法定理
\( \sin(\theta+\alpha)=\sin\theta\cos\alpha+\cos\theta\sin\alpha\)
を意識しているからです。
2つを比べると
\( \cos\alpha=\displaystyle \frac{1}{\sqrt{2}}\hspace{10pt},\hspace{10pt} \sin\alpha=\displaystyle \frac{1}{\sqrt{2}}\)
となりますがこれを満たすのは
\( \alpha=\displaystyle \frac{\pi}{4}\)
だから
\( \sin\theta+\cos\theta\\ \\
=\sqrt{2}\left(\sin\theta\cdot\displaystyle \frac{1}{\sqrt{2}}+\cos\theta\cdot\displaystyle \frac{1}{\sqrt{2}}\right)\\ \\
=\sqrt{2}\sin\left(\theta+\displaystyle \frac{\pi}{4}\right)\)
と合成できます。
いくつか練習して合成できるようになっておきましょう。
\( \sin\theta+\sqrt{3}\cos\theta\)
を合成してみましょう。
それぞれの係数から
\( \sqrt{1^2+(\sqrt{3})^2}=2\)
これは最初にやってください。
次に
\( \sin\theta+\sqrt{3}\cos\theta\\ \\
=\underline{2\left(\sin\theta\cdot\displaystyle \frac{1}{2}+\cos\theta\cdot\displaystyle \frac{\sqrt{3}}{2}\right)}\)
これを書かずに合成している高校生にたくさん出会いましたが、これは書いて下さい。
もちろん書かずに合成できるようになればかまいませんが、
加法定理を利用するので書いた方が最終的には広く使えるようになります。
今は合成できるようになることが目的なので書いて下さい。
\( \sin\theta\cdot\displaystyle \frac{1}{2}+\cos\theta\cdot\displaystyle \frac{\sqrt{3}}{2}\)
と加法定理
\( \sin(\theta+\alpha)=\sin\theta\cos\alpha+\cos\theta\sin\alpha\)
を比べて
\( \cos\alpha=\displaystyle \frac{1}{2}\hspace{10pt},\hspace{10pt}\sin\alpha=\displaystyle \frac{\sqrt{3}}{2}\)
の両方を満たすのは
\( \alpha=\displaystyle \frac{\pi}{3}\)
よって
\( \sin\theta+\sqrt{3}\cos\theta\\ \\
=2\left(\sin\theta\cdot\displaystyle \frac{1}{2}+\cos\theta\cdot\displaystyle \frac{\sqrt{3}}{2}\right)\\ \\
=2\sin\left(\theta+\displaystyle \frac{\pi}{3}\right)\)
次は、さっきと似た係数だけど \( \alpha \) が変わります。
\( \sqrt{3}\sin\theta+\cos\theta\\ \\
=\underline{2\left(\sin\theta\cdot\displaystyle \frac{\sqrt{3}}{2}+\cos\theta\cdot \displaystyle \frac{1}{2}\right)}\\ \\
=2\sin\left(\theta+\displaystyle \frac{\pi}{6}\right)\)
出てくる数値は同じですが
\( \cos\alpha =\displaystyle \frac{\sqrt{3}}{2}\hspace{10pt}.\hspace{10pt}\sin\alpha=\displaystyle \frac{1}{2}\)
なのでさっきの合成とは違いますよ。
下線を引いている加法定理の形を書き出すことと、
\(\sin\alpha \,,\,\cos\alpha \)の値を書き出して
\( \alpha \) を求めさえすれば良いということです。
もう一つ、今度は符号を変えて見ましょう。
\( \sqrt{a^2+b^2}\) の部分は変わりません。
\( \sin\theta -\cos\theta\\ \\
=\sqrt{2}\left(\sin\theta\cdot\displaystyle \frac{1}{\sqrt{2}}-\cos\theta\cdot\displaystyle \frac{1}{\sqrt{2}}\right)\)
ここからはふた通りありますが加法定理を最小限しか覚えていないとして今までと同じ方法でやります。
\( \sin\theta -\cos\theta\\ \\
=\sqrt{2}\left(\sin\theta\cdot\displaystyle \frac{1}{\sqrt{2}}-\cos\theta\cdot\displaystyle \frac{1}{\sqrt{2}}\right)\\ \\
=\sqrt{2}\left(\sin\theta\cdot\displaystyle \frac{1}{\sqrt{2}}+\cos\theta\cdot\displaystyle \frac{-1}{\sqrt{2}}\right)\)
と見れば
\( \cos\alpha=\displaystyle \frac{1}{\sqrt{2}}\hspace{10pt}.\hspace{10pt}\sin\alpha=-\displaystyle \frac{1}{\sqrt{2}}\)
これを両方満たすのは
\( \alpha=-\displaystyle \frac{\pi}{4}\)
です。
これを加法定理
\( \sin(\theta+\alpha)=\sin\theta\cos\alpha+\cos\theta\sin\alpha\)
にあてはめれば
\( \sin\left\{\theta+\left(-\displaystyle \frac{\pi}{4}\right)\right\}=\sin\left(\theta-\displaystyle \frac{\pi}{4}\right)\)
とすることもできます。
定理のもう1段階先を覚えていて
\( \sin(\theta-\alpha)=\sin\theta\cos\alpha-\cos\theta\sin\alpha\)
を利用出来るなら
\( \sin\theta -\cos\theta\\ \\
=\sqrt{2}\left(\underline{\sin\theta\cdot\displaystyle \frac{1}{\sqrt{2}}-\cos\theta\cdot\displaystyle \frac{1}{\sqrt{2}}}\right)\)
から即座に
\( \sin\left(\theta-\displaystyle \frac{\pi}{4}\right)=\underline{\sin\theta\cdot\displaystyle \frac{1}{\sqrt{2}}-\cos\theta\cdot\displaystyle \frac{1}{\sqrt{2}}}\)
とつなげて
\( \sin\theta -\cos\theta=\sqrt{2}\sin\left(\theta-\displaystyle \frac{\pi}{4}\right)\)
と合成できます。
合成を適当にやっていると符号が合わないことが出てきますので注意しておきましょう。
ここでは \( \alpha\) が具体的に求まる合成をしました。
これができればそれで良いです。
一応 \( \alpha \) が具体的に出ないときの合成も書いておきますが、定理の通りです。
\( 2\sin\theta-\cos\theta\) を合成してみると
\( 2\sin\theta-\cos\theta\\ \\
=\sqrt{5}\left(\underline{\sin\theta\cdot\displaystyle \frac{2}{\sqrt{5}}+\cos\theta\cdot\displaystyle \frac{-1}{\sqrt{5}}}\right)\)
となりますが、
\(\displaystyle \cos\alpha=\frac{2}{\sqrt{5}}\) や \(\displaystyle\sin\alpha=\frac{-1}{\sqrt{5}}\)
となる \( \alpha\) は定まりません。
このようなときは
\( 2\sin\theta-\cos\theta=\sqrt{5}(\theta+\alpha)\)
と合成し、
「ただし、\( \alpha\) は
\(\displaystyle \cos\alpha=\frac{2}{\sqrt{5}}\,,\,\sin\alpha=\frac{-1}{\sqrt{5}}\) を満たす。」
と添え書きをすれば良いのです。
加法定理を書いて処理すればどちらも同じなのですが、
先ずは具体的に求まる合成からでいいです。
余弦(コサイン)の合成の公式
中にはコサインで合成することすら知らない高校生人もいますが、
できるんですよ。
あんまり使われないので必要無いですが、普通に使えるので見ておいてください。
[合成の公式](コサイン編)
\( a\cos\theta+b\sin\theta=\sqrt{a^2+b^2}\,\cos(\theta-\alpha)\)
ただし、\( \alpha\) は
\( \cos\alpha=\displaystyle \frac{a}{\sqrt{a^2+b^2}}\hspace{10pt},\hspace{10pt}\sin\alpha=\displaystyle \frac{b}{\sqrt{a^2+b^2}}\)
を満たす角である。
加法定理を使うのは同じですが、
\( \cos(\theta+\alpha)=\cos\theta\cos\alpha-\sin\theta\sin\alpha\)
を利用します。
例えば、
\( \cos\theta+\sin\theta\\ \\
=\sqrt{2}(\cos\theta\cdot\displaystyle \frac{1}{\sqrt{2}}+\sin\theta\cdot\displaystyle \frac{1}{\sqrt{2}})\\ \\
=\sqrt{2}(\underline{\cos\theta\cdot\displaystyle \frac{1}{\sqrt{2}}-\sin\theta\cdot\displaystyle \frac{-1}{\sqrt{2}}})\)
ここで加法定理
\( \cos(\theta+\alpha)=\underline{\cos\theta\cos\alpha-\sin\theta\sin\alpha}\)
と比べて、
\( \cos\alpha=\displaystyle \frac{1}{\sqrt{2}}\hspace{10pt},\hspace{10pt}\sin\alpha=\displaystyle \frac{-1}{\sqrt{2}}\)
となる \( \alpha\) を定めると
\( \alpha=-\displaystyle \frac{\pi}{4}\)
よって
\( \cos\theta+\sin\theta=\sqrt{2}\cos\left(\theta-\displaystyle \frac{\pi}{4}\right)\)
とコサインで合成することも難しい訳ではありません。
合成は正弦(サイン)でできれば十分です。
しかし、サインでの合成も出来ないかも、という最悪の場合、
\( a\sin\theta+b\cos\theta=\sqrt{a^2+b^2}\,\sin(\theta+\alpha)\)
となることを想定して \( \alpha\) を探す方法でも良いです。
三角関数では「加法定理」か「合成」は確実に使います。
「加法定理を覚えていない」ことと、この「合成ができない」ということは、三角関数を捨てているのと同じことです。
三角関数がどうしても苦手という人はこの2つをやり直してみてください。
もしかしたら、目の前が少しは明るくなるかもしれません。
覚えることが多い単元ですので根気よく粘ってください。笑