三角関数は三角比の性質そのままに角度が拡張されます。
さらに、関数としてあつかうのでグラフを見なければならないことと加法定理の応用が加わるので少し覚えることが増えます。
ここでは応用になりますが数学Ⅲまでやるなら和と積の公式まで覚えておく方がいいです。
三角関数の要点
基本的な性質や用語は三角比と同じなのでさっさと進めます。
三角比と違うのは関数として扱うのでグラフが出てくることです。
角の拡張（弧度法と一般角）
三角比では角の大きさを度分法で扱ってきましたが、
三角関数では弧度法を使います。
\(\color{red}{\fbox{ 弧度法 }}\)
半径\(\,1\,\)の円である単位円において、
弧の長さが\(\,1\,\)の円弧を見込める中心角を\(\,1\,\)ラジアンという。
単位円において、
弧の長さが\(\,\color{red}{\ell}\,\)となる中心角は\(\,\color{blue}{\ell}\,\)ラジアン
です。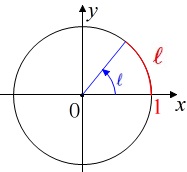
覚えやすいのは単位円の円周が\(\,2\pi\,\)なので
\(\displaystyle \color{red}{360^{\circ}=2\pi (ラジアン)} \)
を基準にして比例で考える方法です。
この単位、左辺は「°（度）」ですが右辺は「ラジアン」でおかしな感じがしますが、
数学\(\,Ⅱ\,\)の三角関数のように弧度法（ラジアン）で扱っていることが分かっているときは省略するのが普通なので書かなくて良いです。
\(\hspace{10pt}\displaystyle 180^{\circ}=\pi\,,\,90^{\circ}=\frac{\pi}{2}\)
\(\color{red}{\fbox{ 一般角 }}\)
1つの動径が表す角を一般角という。
1つの動径があれば、\(\,1\,\)周しても\(\,2\,\)周しても同じ動径を表すのでまとめて表すことができるということです。
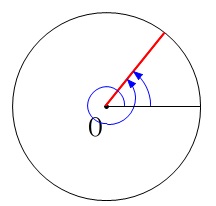
\(\color{red}{\fbox{ 一般角の表し方 }}\)
始線となす角の1つを\(\,\theta\,\)とすると一般角は
\(\hspace{10pt}\color{red}{\theta+2\,n\,\pi (\,n\,は整数\,)}\)
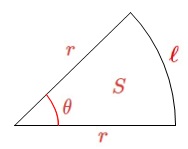
弧度法を用いると弧の長さと扇形の面積が簡単に表せます。
\(\color{red}{\fbox{ 弧の長さと扇形の面積の公式 }}\)
半径\(\,r\,\)、中心角\(\,\theta\,\)とすると
弧の長さ \(\,\ell=r\,\theta\,\)
扇形の面積 \(\displaystyle \,S=\frac{1}{2}\,r^2\,\theta=\frac{1}{2}\,\ell\,\theta\,\)
これは三角比または中学数学で同じように使える公式なので覚えておきましょう。
三角関数
三角関数の定義だけまとめておきます。
\(\color{red}{\fbox{ sin , cos , tan 関数 }}\)
単位円において原点\(\,\mathrm{O}\,\)を基準点とし、\(\,x\,\)軸の性の部分を始線として、
一般角\(\,\theta\,\)の動径を描き単位円との交点を\(\,\mathrm{P}\,\)とする。
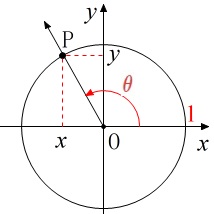このとき\(\,\mathrm{P}\,\)の座標\(\,x,y\,\)はともに角\(\,\theta\,\)の関数であり、
\(\,x=\cos \,\theta\,,\,y=\sin \,\theta\,\)
と定める。
\(\hspace{10pt}\sin\,\theta\) をサイン関数
\(\hspace{10pt}\cos\,\theta\) をコサイン関数
という。
また、\(\cos\,\theta ≠0\) であるような\(\,\theta\,\)について
\(\hspace{10pt}\displaystyle \tan\,\theta=\frac{\sin\,\theta}{\cos\,\theta}\)
により、\(\,\tan\,\theta\,\)が定義される。
\(\,\tan\,\theta\,\)を\(\,\theta\,\)のタンジェント関数という。
これが単位円を用いた定義です。
次はグラフです。
三角関数のグラフ
三角関数のグラフは横軸は\(\,\theta\,\)です。
\(\hspace{10pt}y=\sin\,\theta\) のグラフ
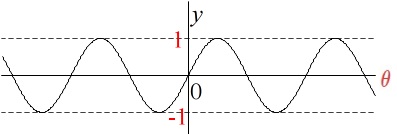原点に関して対称です。
\(\hspace{10pt}y=\cos\,\theta\) のグラフ
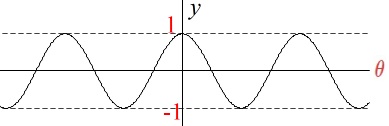\(\,y\,\)軸に関して対称です。
\(\hspace{10pt}y=\tan\,\theta\) のグラフ
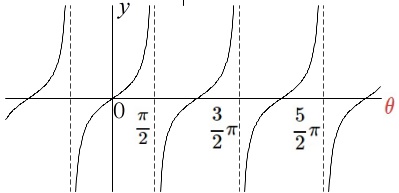原点に関して対称になります。
\(\,n\,\)を整数として\(\hspace{10pt}\displaystyle \theta=\frac{\pi}{2}+n\,\pi\,\)は漸近線です。
\(\color{red}{\fbox{ 三角関数のグラフの周期 }}\)
\(\,k\,\)を正の定数とするとき
\(\,\sin\,k\theta\,,\,cos\,k\theta\,\)の周期は \(\displaystyle \frac{2\,\pi}{k}\)
\(\,tan\,\theta\,\)の周期は \(\displaystyle \frac{\pi}{k}\)
となる。
これは実際にグラフを書く練習をしないと言っている意味は分かりません。
教科書の例題でも良いから\(\,k\,\)に具体的な値を入れ、グラフを書いて意味がつかめるまで試して見てください。
（ここでは一つひとつやっていくと長くなるので省略します。笑）
三角関数の性質
三角関数において成り立つ等式を並べておきます。
（三角比でも出てきているので簡単にまとめるだけにしておきます。）
\(\,\sin\,,\,\cos\,,\,\tan\,\)の符号は象限で決まっています。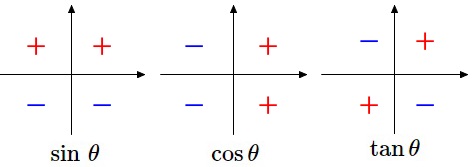
これを覚えておけば\(\,\theta\,\)が第\(\,1\,\)象限のときの値さえ覚えておけばすべての象限で値が出せます。
周期から
\( \begin{cases}
\hspace{7pt} \sin(\,\theta+2n\pi)=\sin\,\theta\\ \\
\hspace{7pt} \cos (\,\theta+2n\pi)=\cos \theta\\ \\
\hspace{7pt} \tan (\,\theta+\color{red}{n\pi})=\tan \theta
\end{cases}\)
（\(\,n\,\)は整数です。）
\((\,-\theta\,)\)を第\(\,4\,\)象限と見なして、
\( \begin{cases}
\hspace{7pt} \sin(\,-\theta\,)=\color{red}{-}\sin\,\theta\\ \\
\hspace{7pt} \cos (\,-\theta\,)=\cos \theta\\ \\
\hspace{7pt} \tan (\,-\theta\,)=\color{red}{-}\tan \theta
\end{cases}\)
\(\,(\,\pi-\theta)\,\)を第\(\,2\,\)象限と見なして
\( \begin{cases}
\hspace{7pt} \sin(\,\pi-\theta)=\sin\,\theta\\ \\
\hspace{7pt} \cos (\,\pi-\theta)=\color{red}{-}\cos \theta\\ \\
\hspace{7pt} \tan (\,\pi-\theta)=\color{red}{-}\tan \theta
\end{cases}\)
\(\,(\,\pi+\theta)\,\)を第\(\,3\,\)象限と見なして
\( \begin{cases}
\hspace{7pt} \sin(\,\pi+\theta)=\color{red}{-}\sin\,\theta\\ \\
\hspace{7pt} \cos (\,\pi+\theta)=\color{red}{-}\cos \theta\\ \\
\hspace{7pt} \tan (\,\pi+\theta)=\tan \theta
\end{cases}\)
\(\,\sin\,,\,\cos\,\)が入れかわりますが\(\displaystyle \left(\,\frac{\pi}{2}-\theta \,\right)\)を第\(\,1\,\)象限と見なして
\( \begin{cases}
\hspace{7pt}\displaystyle \sin\left(\,\frac{\pi}{2}-\theta\right)=\cos\,\theta\\ \\
\hspace{7pt}\displaystyle \cos \left(\,\frac{\pi}{2}-\theta\right)=\sin \theta\\ \\
\hspace{7pt}\displaystyle \tan \left(\,\frac{\pi}{2}-\theta\right)=\frac{1}{\tan \theta}
\end{cases}\)
これも\(\,\sin\,,\,\cos\,\)が入れかわりますが\(\displaystyle \left(\,\theta +\frac{\pi}{2}\,\right)\)を第\(\,2\,\)象限と見なして
\( \begin{cases}
\hspace{7pt}\displaystyle \sin\left(\,\theta +\frac{\pi}{2}\right)=\cos\,\theta\\ \\
\hspace{7pt}\displaystyle \cos \left(\,\theta +\frac{\pi}{2}\right)=\color{red}{-}\sin \theta\\ \\
\hspace{7pt}\displaystyle \tan \left(\,\theta +\frac{\pi}{2}\right)=\color{red}{-}\frac{1}{\tan \theta}
\end{cases}\)
三角比でさんざん使った関係式は当然成り立ちます。
\(\hspace{10pt}\displaystyle \frac{\sin\,\theta}{\cos\,\theta}=\tan\,\theta\)
\(\hspace{10pt}\sin^2\theta+\cos^2\theta=1\)
これを両辺\(\,\cos^2\,\theta\,\)で割った
\(\hspace{10pt}\displaystyle \tan^2\theta+1=\frac{1}{\cos^2\,\theta}\)
ここまでの内容は問題解説の中で確認してください。
三角比と三角関数は扱う角の範囲の違いと、関数なのでグラフが関係してくることです。
関係式は同じなので三角比で忘れていることはないかしっかり確認しておきましょう。
加法定理の要点
三角関数の公式がいろいろと出てきますが、基本は加法定理です。
（加法定理は確率にもありますがここでは三角関数の「加法定理」と読み取っておいてください。）
三角関数の加法定理
\(\color{red}{\fbox{ 正弦、余弦の加法定理 }}\)
\(\hspace{10pt}\color{red}{\sin\,(\alpha+\beta\,)=\sin\alpha\cos\beta+\cos\alpha\sin\beta} ･･･①\)
\(\hspace{10pt}\color{blue}{\sin\,(\alpha-\beta\,)=\sin\alpha\cos\beta-\cos\alpha\sin\beta} ･･･②\)
\(\hspace{10pt}\color{red}{\cos\,(\alpha+\beta\,)=\cos\alpha\cos\beta-\sin\alpha\cos\beta} ･･･③\)
\(\hspace{10pt}\color{blue}{\cos\,(\alpha-\beta\,)=\cos\alpha\cos\beta+\sin\alpha\cos\beta} ･･･④\)
②④は①③において\(\,\beta\,\)の代わりに\(\,(-\beta)\,\)とすれば
\(\hspace{10pt}\color{red}{\sin\,(-\beta)}=\color{blue}{-\sin\beta}\)
となるだけなので①③を覚えていれば導けます。
\(\color{red}{\fbox{ 正接の加法定理 }}\)
\(\hspace{10pt}\displaystyle \color{red}{\tan(\alpha+\beta)=\frac{\tan\alpha+\tan\beta}{1-\tan\alpha\tan\beta}} ･･･⑤\)
\(\hspace{10pt}\displaystyle \color{blue}{\tan(\alpha+\beta)=\frac{\tan\alpha+\tan\beta}{1-\tan\alpha\tan\beta}} ･･･⑥\)
⑥は⑤において\(\,\color{red}{\beta}\,\)を\(\,(\color{blue}{-\beta})\,\)とすれば
\(\hspace{10pt}\color{red}{\tan(-\beta)}=\color{blue}{-\tan\beta}\)
なので⑤を覚えておけばなんとかなります。
\(\,2\,\)直線のなす角をタンジェントの加法定理を用いて求める問題もよくあります。
ちょっとした応用ですが、なす角を図示すると分かり易くなります。
加法定理の応用
２倍角と半角の公式と合成ですが、３倍角も覚えておくと後が楽になりますよ。
\(\color{red}{\fbox{ 正弦、余弦の２倍角の公式 }}\)
\(\hspace{10pt}\color{red}{\sin(\,2\,\alpha\,)=2\,\sin\alpha\cos\alpha}\)
\(\hspace{8pt}\begin{eqnarray}
\color{red}{\cos(\,2\,\alpha\,)}&=&\cos^2\alpha-\sin^2\alpha\\
&=&\color{red}{1-2\,\sin^2\alpha}\\
&=&\color{blue}{2\,\cos^2\alpha-1}
\end{eqnarray}\)
\(\color{red}{\fbox{ 正接の２倍角の公式 }}\)
\(\hspace{10pt}\displaystyle \color{red}{\tan(\,2\alpha\,)=\frac{2\tan\alpha}{1-\tan^2\alpha}}\)
コサインの２倍角は３通りとも使うので覚えておきましょう。
⇒ 三角関数の２倍角と３倍角の公式と三角方程式、不等式の解き方
３倍角の公式は確認しておきましょう。
係数が似ているので気をつけてください。
\(\color{blue}{\fbox{ 正弦、余弦、正接の半角の公式 }}\)
\(\hspace{10pt}\displaystyle \color{blue}{\sin^2\frac{\alpha}{2}=\frac{1-\cos\alpha}{2}}\)
\(\hspace{10pt}\displaystyle \color{blue}{\cos^2\frac{\alpha}{2}=\frac{1+\cos\alpha}{2}}\)
\(\hspace{10pt}\displaystyle \color{blue}{\tan^2\frac{\alpha}{2}=\frac{1-\cos\alpha}{1+\cos\alpha}}\)
これらは\(\,2\,\)倍角の公式において、
\(\color{red}{\alpha}\,\)を\(\displaystyle \,\color{blue}{\frac{\alpha}{2}}\,\) （\(\,\color{red}{2\,\alpha}\,\)を\(\,\color{blue}{\alpha}\,\)）
と置きかえることで導かれます。
\(\color{red}{\fbox{ 三角関数の合成 }}\)
\(\hspace{10pt}\displaystyle \color{red}{a\sin\theta+b\cos\theta=\sqrt{a^2+b^2}\sin(\,\theta+\alpha}\,)\)
ただし、\(\,\color{blue}{\alpha}\,\)は
\(\displaystyle \,\color{blue}{\cos\alpha=\frac{\alpha}{\sqrt{a^2+b^2}}\,,\,\sin\alpha=\frac{b}{\sqrt{a^2+b^2}}}\,\)
を満たす角である。
これは慣れた方が早いです。
三角関数でも最大値最小値問題はよく問われます。
和と積の公式
加法定理を利用すれば正弦と余弦の積を和に変形することができます。
\(\color{red}{\fbox{ 積を和に直す公式 }}\)
\(\hspace{10pt}\displaystyle \color{red}{\sin\alpha}\color{blue}{\cos\beta}=\color{red}{\frac{1}{2}\{\sin(\alpha+\beta)+\sin(\alpha-\beta)\}} ･･･①\)
\(\hspace{10pt}\displaystyle \color{blue}{\cos\alpha}\color{red}{\sin\beta}=\color{red}{\frac{1}{2}\{\sin(\alpha+\beta)-\sin(\alpha-\beta)\}} ･･･②\)
\(\hspace{10pt}\displaystyle \color{blue}{\cos\alpha}\color{blue}{\cos\beta}=\color{red}{\frac{1}{2}\{\cos(\alpha+\beta)+\cos(\alpha-\beta)\}} ･･･③\)
\(\hspace{10pt}\displaystyle\color{red}{ \sin\alpha}\color{red}{\sin\beta}=\color{red}{-\frac{1}{2}\{\cos(\alpha+\beta)-\cos(\alpha-\beta)\}} ･･･③\)
①②③④において
\(\,\alpha+\beta=A\,,\,\alpha-\beta=B\,\)
とおくと
\(\displaystyle \,\alpha=\frac{A+B}{2}\,,\,\beta=\frac{A-B}{2}\,\)
と変形できることから和を積に直す公式が導かれます。
\(\color{red}{\fbox{ 和を積に直す公式 }}\)
\(\hspace{10pt}\displaystyle \color{red}{\sin A+\sin B=2\,\sin\frac{A+B}{2}\cos\frac{A-B}{2}}\)
\(\hspace{10pt}\displaystyle \color{red}{\sin A-\sin B=2\,\cos\frac{A+B}{2}\sin\frac{A-B}{2}}\)
\(\hspace{10pt}\displaystyle \color{red}{\cos A+\cos B=2\,\cos\frac{A+B}{2}\cos\frac{A-B}{2}}\)
\(\hspace{10pt}\displaystyle \color{red}{\cos A-\cos B=-2\,\sin\frac{A+B}{2}\sin\frac{A-B}{2}}\)
⇒ 三角関数の和（差）を積に直す公式の証明とその応用
\(\,A\,,\,B\,,\,A+B\,,\,A-B\,\)の位置は同じなので覚えられると便利です。
⇒ 共通テスト(センター試験)数学の勉強法と対策まとめ単元別攻略と解説
共通テストではグラフを扱うことが少ないですが、
関数ですのでグラフはイメージできるようになっておいた方が良いですよ。