対数で底や真数に未知数を持っている対数方程式の解き方です。
指数方程式と同じように置き換えができれば普通に方程式を解くのと同じですが、底の変換や真数条件についてしっかりチェックすることが大切です。
対数関数のグラフは不等式のときに使うことが多いですが方程式でも使うのでグラフの書き方についても触れてもおきます。
対数方程式を解くとき最初にやるべきこと
対数の方程式です。
問題は対数方程式だけ取り上げていますが指数方程式と方針は同じです。
対数方程式で初めにチェックしなければならないのは、『真数条件』です。
方程式を変形させる前に、必ずチェックしましょう。
変形させた後ではダメです。
例えば、
\( \log_{2}x^2\) の真数は \( x^2\) です。
真数条件は \( x^2\,＞\,0\) となります。
\( \log_{2}x^2\,=2\log_{2}x\)
とできるのは \( x\,＞\,0\) のときだけですよ。
ここでややこしくしてもしかたないので先に進みますが、真数条件は変形する前の形で取り上げておいてください。
次の方程式を解け。
（１） \( \log_{2}3x + \log_{2}(x-1) =2+\log_{2}(x-1)^2\)
（２） \( ( \log_{2}x^2)^2 +8 (\log_{2}x -4)=0\)
（１） \( \log_{2}3x + \log_{2}(x-1) =2+\log_{2}(x-1)^2\)
対数方程式を解くときに最初にしなければならないのは「真数条件」を調べておくことです。
真数条件は「真数すべてが正」なので
\(\hspace{10pt} 3x>0\,,\,(x-1)>0\,,\,(x-1)^2>0\)
です。
これらは「かつ」なので、
\( x>1\) ･･･①
これが『真数条件』となります。
次にすることは、底をそろえることですが既にそろっているので必要無くて、
\(\begin{eqnarray} \log_{2}3x + \log_{2}(x-1) &=&2+\log_{2}(x-1)^2\\ \\
\hspace{5pt} \Leftrightarrow \hspace{30pt} \log_{2}3x(x-1)&=& \log_{2}4 +\log_{2}(x-1)^2\\ \\
\hspace{5pt} \Leftrightarrow \hspace{30pt} \log_{2}3x(x-1)&=& \log_{2}4(x-1)^2
\end{eqnarray}\)
対数の値は、\(\,x\,\)の値１つに対し１つしか存在しないので、真数同士が等しくなります。
よって
\(\begin{eqnarray} 3x(x-1)&=&4(x-1)^2\\ \\
\Leftrightarrow \hspace{32pt} 3x^2-3x&=&4(x^2-2x+1)\\ \\
\Leftrightarrow \hspace{32pt} 3x^2-3x&=&4x^2-8x+4\\ \\
\Leftrightarrow \hspace{12pt} -x^2+5x-4&=&0\\ \\
\Leftrightarrow \hspace{20pt} x^2-5x+4&=&0\\ \\
\Leftrightarrow \hspace{10pt} (x-1)(x-4)&=&0
\end{eqnarray}\)
から
\(\hspace{10pt} x=1\,,\,4\)
となりますが、真数条件①から \( x=1\) は不適となります。
\( \underline{ x=4 }\)
左辺にすべての項を集めても良いですが、真数の比較の方が早いでしょう。
対数方程式のグラフ利用
（２） \( ( \log_{2}x^2)^2 +8 (\log_{2}x -4)=0\)
これも（１）と同じで真数条件から求めておきます。
\( x^2>0\) かつ \(x>0\)
これらから \( x>0\) ･･･②
ここで、\(\log_{2}x\) 部分が同じなので、\( \log_{2}x = t\) とおくと、
\( \color{red}{t}\) は実数全体となります。
置換（置きかえ）した \( t\) の変域には注意して下さい。
対数のグラフから考えれば分かりますので、少し指数･対数のグラフについて触れておきます。
教科書にある基本なので覚えているとは思いますが、復習しておきます。
指数関数のグラフ
\(y=a^x\) のグラフは「底」の値によって変わります。
ⅰ） \( a>1\) のとき
例えば
\( y=2^x\)
を見てみると
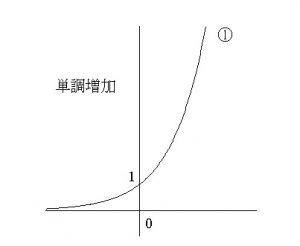
\( x=-1\,,\,0\,,\,1\,,\,2\,,\,\cdots\)
と \( x\) の値が大きくなれば \( y\) の値も大きくなります。
これを増加関数といいます。
ⅱ） \( 0< a < 1\) のとき
例えば
\( y=\left(\displaystyle \frac{1}{2}\right)^x\)
を見てみると
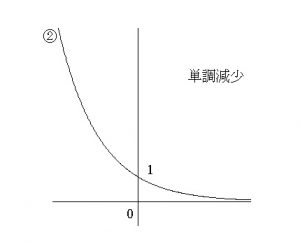
\( x=-1\,,\,0\,,\,1\,,\,2\,,\,\cdots\)
と \(x\) の値が大きくなれば \( y\) の値は小さくなります。
これを減少関数といいます。
ただし、どちらも必ず \( x=0\,,\,y=1\) つまり \( \color{red}{(0\,,\,1)}\) を通ります。
これが基本のグラフとなるので平行移動させる場合もこれを基本にして下さい。
底 \( a\) は \( a>0 , a\neq 1\) なので定義から確認しておきましょう。
対数関数のグラフ
対数関数\(\, y=\log_{a}x\,\)のグラフは、
ⅲ） \( a>1\) のとき
例えば、\(\, y=\log_{2}x\,\)を見てみると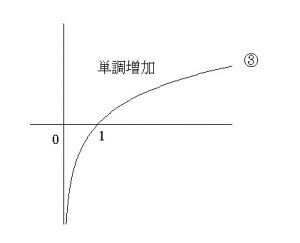
\( x=1\,,\,2\,,\,\cdots\)
（ \( x>0\) ）
と\(\,x\,\)の値が大きくなれば\(\, y\,\)の値も大きくなります。
これも指数関数同様に増加関数といいます。
ⅳ） \( 0< a < 1\) のとき
例えば、\(\,\displaystyle y=\log_{\frac{1}{2}}x\,\)を見てみると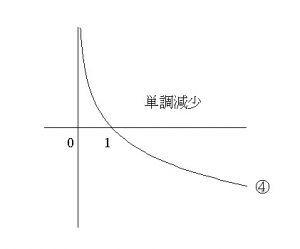
\(\hspace{10pt}x=1\,,\,2\,,\,\cdots\)
（\(\hspace{10pt} x>0\) ）
と\(\, x\,\)の値が大きくなれば\(\, y\,\)の値は小さくなります。
これを減少関数といいます。
ただし、どちらも必ず \(\, x=1\,,\,y=0\,\)つまり\( \color{red}{(\,1\,,\,0\,)}\)を通ります。
指数関数と同じようにこれが基本のグラフとなるので平行移動させる場合もこれを基本にして下さい。
底 \( a\) は \( a>0\,,\,a\neq 1\) なのでこれも定義から確認しておいて下さい。
指数関数の逆関数なので当然ですね。
\( y=a^x\) と \( \log_{a}x\) のグラフの関係は、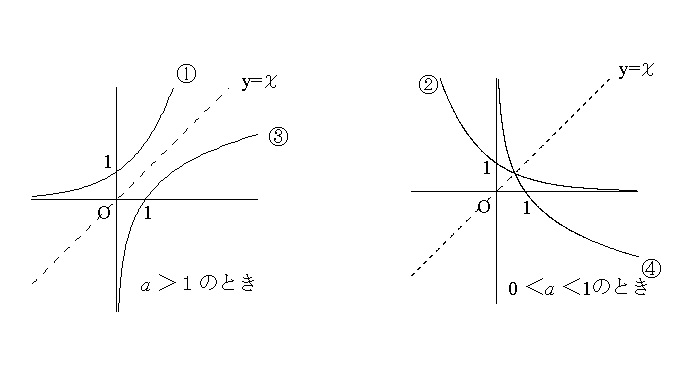
と、\( \,y=x\,\) に関して対称であるということも確認しておきましょう。
対数方程式の答を出す前の確認事項
では、
\(\hspace{10pt} ( \log_{2}x^2)^2 +8 ( \log_{2} x -4 ) = 0\)
を解いて行きます。
\(\log_{2} x = t\) とおくと \( \color{red}{t}\,\)は実数全体で、
\(\hspace{10pt} ( \log_{2}x^2)^2 +8 ( \log_{2} x -4 ) = 0\\ \\
\hspace{5pt} \Leftrightarrow \hspace{5pt} (2\log_{2}x)^2+8(\log_{2}x-4)=0\\ \\
\hspace{5pt} \Leftrightarrow \hspace{5pt} (2t)^2+8t-32=0\\ \\
\hspace{5pt} \Leftrightarrow \hspace{5pt} 4t^2+8t-32=0\\ \\
\hspace{5pt} \Leftrightarrow \hspace{5pt} t^2+2t-8=0\\ \\
\hspace{5pt} \Leftrightarrow \hspace{5pt} (t+4)(t-2)=0\\ \\
\hspace{5pt} \Leftrightarrow \hspace{5pt} t=\color{red}{-4}\,,\,\color{blue}{2}\)
置換して\(\,\log_{2}x=t\,\)としましたが、解は\(\, x\,\) で求めます。
\( \color{red}{t=-4}\) のとき
\(\hspace{10pt}\log_{2}x=-4\\ \\
\Leftrightarrow \hspace{10pt}\log_{2}x=\log_{2}2^{-4}\)
だから
\( x=2^{-4}=\displaystyle \frac{1}{16}\)
\( \color{blue}{t=2}\) のとき
\(\hspace{10pt} \log_{2}x=2\\ \\
\Leftrightarrow \hspace{10pt}\log_{2}x=\log_{2}2^2\)
だから
\(\hspace{10pt}x=2^{2}=4\)
以上より
\( x=\underline{\displaystyle \frac{1}{16}\,,\,4 }\)
対数方程式を解くときは、真数条件を一番先に出しておくようにしましょう。
でも同じですが、それほど特殊な解き方がある訳ではありませんよ。
対数は、指数の別表現に過ぎないのです。