指数に未知数を含む不等式の解き方です。
まとまっている数を置き換えして解くのは方程式の場合と同じですが、
不等式は大小関係でもあるのでグラフを利用すると簡単に解ける問題が多いです。
指数関数のグラフは底の大きさでふた通りあることをもう一度確認しておきましょう。
指数関数のグラフをもう一度確認しておきましょう。
指数関数のグラフ
指数関数 \(y=a^x\) のグラフは底の大きさでふた通りに分けられます。
\( a>1\) のとき増加関数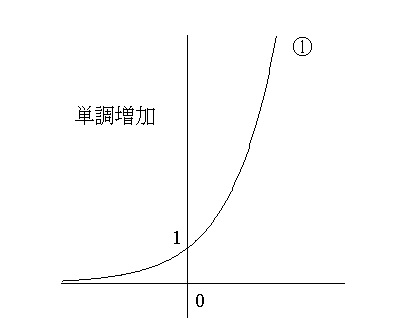 
\( 0< a < 1\) のとき減少関数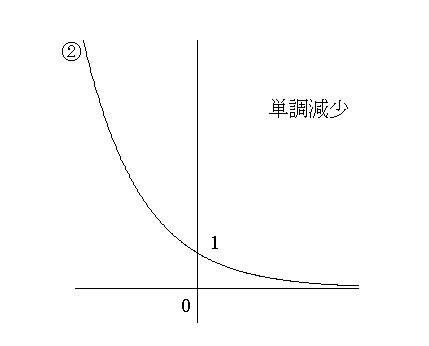
となります。
不安な人は
で確認しておいてください。
指数関数のグラフの書き方もまとめてあります。
不等式にどのように利用出来るかというと、
ⅰ）底が１より大きいとき
「指数が大きくなれば指数で表された数全体が大きくなる。」
これは
「指数で表された数全体が大きいなら指数も大きい」
ということになります。
\( 3^x>3^y \hspace{5pt} \Leftrightarrow \hspace{5pt} x>y\)
ⅱ）底が１より小さいとき
「指数が大きくなれば指数で表された数全体が小さくなる。」
「指数で表された数全体が小さいなら逆に指数は大きくなる。」
ということになります。
\( \left(\displaystyle \frac{1}{2}\right)^x>\left(\displaystyle \frac{1}{2}\right)^y \hspace{5pt} \Leftrightarrow \hspace{5pt} x\,< \,y\)
このことさえわかっていれば、置換して方針を決めておけば普通の不等式です。
指数不等式の解き方
問題を解いて行きましょう。
次の不等式を解け。
（１） \( 3^{2x+1}+2\cdot 3^x>1\)
（２） \(\displaystyle \left(\frac{1}{4}\right)^x+8 ≦ 3\cdot \left(\frac{1}{2}\right)^{x-1}\)
底が１より大きい指数方程式の解き方
（１） \( 3^{2x+1}+2\cdot 3^x>1\)
指数を見るのは後です。
先ずは底がそろっているかどうかを見ます。
底は３でそろっているので、置換できるようにまとまりを探します。
\(\hspace{10pt} 3^{2x+1}+2\cdot 3^x>1\\ \\
\Leftrightarrow \hspace{5pt} 3\cdot 3^2x+2\cdot 3^x>1\\ \\
\Leftrightarrow \hspace{5pt} 3\cdot (3^x)^2+2\cdot 3^x>1\)
と変形できるので、
\(\color{red}{3^x=t}\) とおくと \( \color{red}{t>0}\) で
\(\hspace{10pt} 3\cdot (3^x)^2+2\cdot 3^x>1\\ \\
\Leftrightarrow \hspace{5pt} 3\cdot t^2+2\cdot t >1\\ \\
\Leftrightarrow \hspace{5pt} 3t^2+2t-1>0\\ \\
\Leftrightarrow \hspace{5pt} (3t-1)(t+1)>0\)
ここで普通なら
「 \( (3t-1)>0 , (t+1)>0\) 」
または
「 \( (3t-1)< 0 , (t+1)< 0\) 」
と場合分けしますが、
真数条件 \( t>0\) から \(\color{red}{(t+1)>0}\) なので
\( (3t-1)>0\) だけを見れば良いのです。
\(\hspace{10pt} 3t-1>0 \hspace{5pt} \Leftrightarrow \hspace{5pt} t>\displaystyle \frac{1}{3}\)
よって
\(\hspace{10pt} 3^x>\displaystyle \frac{1}{3}\\ \\
\hspace{5pt} \Leftrightarrow \hspace{5pt} 3^x > 3^{-1}\)
底が１より大きいので真数の大小はそのまま比較できます。
\( \underline{ x\,＞\,-1 }\)
グラフを簡単に書いてイメージしながら大小関係を見るとわかりやすいですよ。
底が１より小さい指数不等式の解き方
（２） \(\displaystyle \left(\frac{1}{4}\right)^x+8 ≦ 3\cdot \left(\frac{1}{2}\right)^{x-1}\)
指数がうんぬんよりも底がそろっていません。
底をそろえますが、２つ考えてみましょう。
１つは底が１より小さい場合です。
この場合減少関数になるので \( x\) が大きくなるにつれて、\(y\) は小さくなります。
そのための指数の大小が入れかわります。
\(a\,<\,1\) のとき \( a^x\, > \,a^y \Leftrightarrow x < y\)
この性質を利用して解いてみましょう。
\(\hspace{10pt} \left(\displaystyle \frac{1}{4}\right)^x+8 ≦ 3\cdot \left(\displaystyle \frac{1}{2}\right)^{x-1}\\ \\
\hspace{5pt} \Leftrightarrow \hspace{5pt} \left(\displaystyle \frac{1}{2}\right)^{2x}+8≦ 3\cdot \left(\displaystyle \frac{1}{2}\right)^{x-1}\)
これで底がそろったのでまとまりをつくる変形をします。
\(\hspace{10pt} \left(\displaystyle \frac{1}{2}\right)^{2x}+8≦ 3\cdot \left(\displaystyle \frac{1}{2}\right)^{x-1}\\ \\
\hspace{5pt} \Leftrightarrow \hspace{5pt} \left(\displaystyle \frac{1}{2}\right)^{2x}+8≦ 3\cdot \left(\displaystyle \frac{1}{2}\right)^{-1} \left(\displaystyle \frac{1}{2}\right)^{x}\\ \\
\hspace{5pt} \Leftrightarrow \hspace{5pt} \left(\displaystyle \frac{1}{2}\right)^{2x}+8≦ 3\cdot 2^1\cdot \left(\displaystyle \frac{1}{2}\right)^{x}\\ \\
\hspace{5pt} \Leftrightarrow \hspace{5pt} \left(\displaystyle \frac{1}{2}\right)^{2x}+8≦ 6 \left(\displaystyle \frac{1}{2}\right)^{x}\)
ここで
\(\displaystyle \color{red}{\left(\frac{1}{2}\right)^x=t}\) とおくと \( \color{red}{t>0}\) となって不等式は
\( \hspace{10pt}t^2+8≦ 6x\\ \\
\hspace{5pt} \Leftrightarrow \hspace{5pt} t^2-6t+8≦ 0\\ \\
\hspace{5pt} \Leftrightarrow \hspace{5pt} (t-2)(t-4)≦ 0\\ \\
\hspace{5pt} \Leftrightarrow \hspace{5pt} 2 ≦ t ≦ 4\)
つまり
\(\hspace{10pt} 2 ≦ \left(\displaystyle \frac{1}{2}\right)^{x} ≦ 4\\ \\
\hspace{5pt} \Leftrightarrow \hspace{5pt} \left(\displaystyle \frac{1}{2}\right)^{-1} ≦ \left(\displaystyle \frac{1}{2}\right)^{x} ≦ \left(\displaystyle \frac{1}{2}\right)^{-2} \)
底が１より小さいので指数の大小が逆になり、
\( \underline{ -2\,≦\,x\,≦\,-1 }\)
もう一つは、底を１より大きい数で統一します。
\( \left(\displaystyle \frac{1}{4}\right)^x+8 ≦ 3\cdot \left(\displaystyle \frac{1}{2}\right)^{x-1}\\ \\
\hspace{5pt} \Leftrightarrow \hspace{5pt} 2 ≦ \left(\displaystyle \frac{1}{2}\right)^{x} ≦ 4\\ \\
\hspace{5pt} \Leftrightarrow \hspace{5pt} 2 ≦ 2^{-x} ≦ 4\)
とさっき変形したものを利用しても良いのですが、
ここまでは底を１より小さいもので変形しています。
取り組みはじめの方針が違うので、この途中から利用するというのは最初から取り組んだ場合は出てこない形です。
なので最初からやり直します。
仕切り直して底を２にそろえます。
\(\hspace{10pt}\left(\displaystyle \frac{1}{4}\right)^x+8 ≦ 3\cdot \left(\displaystyle \frac{1}{2}\right)^{x-1}\\ \\
\hspace{5pt} \Leftrightarrow \hspace{5pt} (2^{-2})^{x}+8 ≦ 3\cdot (2^{-1})^{x-1}\\ \\
\hspace{5pt} \Leftrightarrow \hspace{5pt} (2^{x})^{-2}+8≦ 3\cdot 2^{-x+1}\\ \\
\hspace{5pt} \Leftrightarrow \hspace{5pt} (2^{x})^{-2}+8≦ 3\cdot 2\cdot 2^{-x}\\ \\
\hspace{5pt} \Leftrightarrow \hspace{5pt} (2^{x})^{-2}+8≦ 3\cdot 2\cdot (2^x)^{-1}\\ \\
\hspace{5pt} \Leftrightarrow \hspace{5pt} \displaystyle \frac{1}{(2^{x})^2}+8 ≦ 6\cdot \displaystyle \frac{1}{2^x}\)
ここで \(2^x=t\) とおくと \( t>0\) で
\(\hspace{10pt} \displaystyle \frac{1}{(2^{x})^2}+8 ≦ 6\cdot \displaystyle \frac{1}{2^x}\\ \\
\hspace{5pt} \Leftrightarrow \hspace{5pt} \displaystyle \frac{1}{t^2}+8 ≦ 6\cdot \displaystyle \frac{1}{t}\)
\(t^2>0\) だから \( t^2\) を両辺にかけても大小関係は変化しないので、
\( \displaystyle \frac{1}{t^2}+8 ≦ 6\cdot \displaystyle \frac{1}{t}\\ \\
\hspace{5pt} \Leftrightarrow \hspace{5pt} 1+8t^2 ≦ 6t\\ \\
\hspace{5pt} \Leftrightarrow \hspace{5pt} 8t^2-6t+1 ≦ 0\\ \\
\hspace{5pt} \Leftrightarrow \hspace{5pt} (4t-1)(2t-1) ≦ 0\\ \\
\hspace{5pt} \Leftrightarrow \hspace{5pt} \displaystyle \frac{1}{4}≦ t ≦ \displaystyle \frac{1}{2}\)
つまり
\( \displaystyle \frac{1}{4}≦ 2^x ≦ \displaystyle \frac{1}{2}\\ \\
\hspace{5pt} \Leftrightarrow \hspace{5pt} 2^{-2} ≦ 2^x ≦ 2^{-1}\)
底が１より大きい増加関数なので指数の大小はそのままで
\( \underline{ -2\,≦\,x\,≦\,-1 }\)
一番見やすいのは、
底を１より小さくして変形途中で出てきた
\( 2 ≦ \left(\displaystyle \frac{1}{2}\right)^{x} ≦ 4\)
と戻したときに、再度、底を２に換える、ということをしたときです。
\(\hspace{10pt} 2 ≦ \left(\displaystyle \frac{1}{2}\right)^{x} ≦ 4\\ \\
\hspace{5pt} \Leftrightarrow \hspace{5pt} 2 ≦ 2^{-x} ≦ 4\\ \\
\hspace{5pt} \Leftrightarrow \hspace{5pt} 2^1 ≦ 2^{-x} ≦ 2^2\\ \\
\hspace{5pt} \Leftrightarrow \hspace{5pt} 1≦ -x ≦ 2\\ \\
\hspace{5pt} \Leftrightarrow \hspace{5pt} -2 ≦ x ≦ -1\)
方針は１つにしたほうがいろいろと考えなくて良いのですが、
一番楽というわけではありません。
底を１より大きくして増加関数で統一して考えるというのは、
一番間違えにくい、というのは事実です。
指数不等式を理解できていれば、対数不等式にもすでに対応できるようになっていますよ。
指数関数と対数関数は逆関数、という定義を忘れなければ意識するのはグラフですね。