微分係数を用いた接線の方程式の求め方を説明します。
接線を求める問題では接点が与えられた曲線上にある場合と、曲線上に無い場合とで少し難易度が変わりますが基本的な手順は同じです。
忘れてはならないことは接線は直線であることなので問題は簡単なものですが基本を確認しておいてください。
ここでは抑えておきたいポイントがいくつかあります。
接線を求めるときは接点が必要
先ず、「接線」は「直線」であること。
何度も言ってきたことですが「接線」とあれば「接点」を探す、もしくは「設定」する。
そして、直線の方程式の置き方ですが、今まではあまり「こう」と決まったやり方をすることは言ってきませんでした。それは、中学数学の１次関数で十分だったからです。
しかし、この微分を扱うときの接線（直線）は形を覚えて下さい。
これは数学\(\,Ⅱ\,\)以上を学習する人にとっては必須事項です！
関数\(\, y=f(x)\,\)上の点\(\, (\color{red}{t}\,,\,\color{red}{f(t)})\,\)における接線の方程式は
\( y-\,\color{red}{f(t)}\,=\,\color{blue}{f'(t)}\,(x-\,\color{red}{t}\,)\) ･･･☆
となります。ややこしくも何ともありません。
今までの考え方で行くと、
傾き\(\,a\,\)で\(\, (\,t\,,\,f(t)\,)\,\)を通る直線が
\(\hspace{10pt} y-f(t)=\color{blue}{a}(x-t)\)
であったのに対し、
傾き\(\, \color{blue}{a}\,\)が\( \,\color{blue}{f'(t)}\,\)に変わっただけです。
（微分係数はその点での接線の傾きです。）
☆の形は必ず覚えてください。
センター試験や共通テストで満点はいらないけど、ある程度は点を取りたいという人でもこれが使えないと話になりません。
いちいちその場で考えるということは数学\(\,Ⅱ\,\)以上ではあまりにも時間がかかるのでできるだけ減らしたいのですが、
もしものときでもその時間は三角関数で使いたいので微分では考える時間は必要無い状態にしておきましょう。
「覚えた」、ということで問題に入りましょう。
曲線 \( y=x^3+4x^2\) 上の点 \( (1\,,\,5)\) における接線を求めよ。
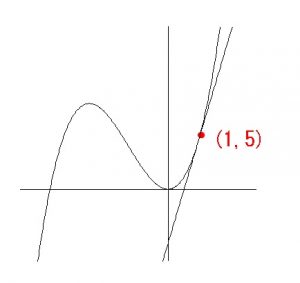これは接点がわかっていますのでものすごく簡単です。\( y=f(x)=x^3+4x^2\)
\( y’=f'(x)=3x^2+8x\)
微分の問題ではこれを書き出しておくことは当たり前にやっておくことです。
接線の傾きは微分係数
接点は \((\,1\,,\,5\,)\) です。
このときの微分係数は
\( f'(1)=3\cdot 1^2+8\cdot 1\,=11\)
この微分係数は接線の傾きです。
求める接線は「傾きが\(\,\color{red}{11}\,\)で\(\,\color{blue}{(\,1\,,\,5\,)}\,\)を通る直線」なので
\(\hspace{10pt} y-\color{blue}{5}=\color{red}{11}(x-\color{blue}{1})\\ \\
\Leftrightarrow \hspace{5pt} \underline{ y=11x-6 }\)
次は接点がわかっていないけど、、、という問題です。
曲線 \( y=x^3-3x\) の接線のうち、
直線 \( y=3x\) に平行なものを求めよ。
これは接点がわかっていませんので先に「接点の設定」です。
接線問題は接点の設定が基本です。
接点がわかっている場合は簡単すぎる問題なんです。
\(\hspace{10pt} y=x^3-3x\)
\(\hspace{10pt} y’=3x^2-3\)
接点の\(\,x\,\)座標を\(\,t\,\)とおくと、
接点は\(\,(\,\color{red}{t}\,,\,\color{red}{t^3-3t}\,)\)
とおけます。
はじめから「接点を\(\,(\,t\,,\,t^3-3t\,)\,\)」とおいても良いですよ。
接線の傾きは\(\,y’\,\)から\(\,\color{blue}{3t^2-3}\,\)で、
接線の方程式は
\(\hspace{10pt} y-(\,\color{red}{t^3-3t}\,)=(\,\color{blue}{3t^2-3}\,)(\,x-\color{red}{t}\,)\) ･･･①
接線は\(\,y=3x\,\)に平行なので傾きが等しいことから
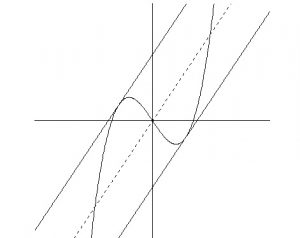（接線が２本あることは予想できます。）
\( 3t^2-3\,=3\)
これを解くと
\(\begin{eqnarray}\displaystyle
3t^2&=&6\\
t^2&=&2\\
t&=&\pm \sqrt{2}
\end{eqnarray}\)
よって①より求める接線は
\( t=\sqrt{2}\) のとき
\(\begin{eqnarray}\displaystyle
y-(2\sqrt{2}-3\sqrt{2})&=&(3\cdot 2-3)(x-\sqrt{2})\\
y+\sqrt{2}&=&3(x-\sqrt{2})\\
y&=&3x-4\sqrt{2}
\end{eqnarray}\)
\( t=-\sqrt{2}\) のとき
\(\begin{eqnarray}\displaystyle
y-(-2\sqrt{2}+3\sqrt{2})&=&(3\cdot 2-3)(x+\sqrt{2})\\
y-\sqrt{2}&=&3(x+\sqrt{2})\\
y&=&3x+4\sqrt{2}
\end{eqnarray}\)
よって求める接線は
\(\hspace{10pt}\displaystyle \underline{ y=3x\pm 4\sqrt{2} }\)
ここでは接点の\( \,x\,\)座標\( \,t\,\)が出た時点で接線の方程式に代入しましたが、
接点を求めてからでもかまいません。
接点はわかっていないけど、接線の傾きがわかっている場合でした。
接点がわかっていないときの設定
次は曲線外の点を通る条件がある接線問題です。
もちろん接点の設定からですが、これができていればいろいろと使えますよ。
曲線 \( y=x^3-4x+2\) に原点から引いた接線の方程式を求めよ。
これも例題２と同じで接点の設定からです。
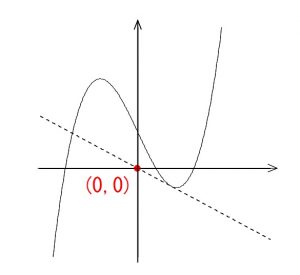原点 \( (\,0\,,\,0\,)\) は曲線上にありません。
問題の「原点から引いた接線」は、原点が接点なのではないことをいっています。
\(\hspace{10pt} y=x^3-4x+2\)
\(\hspace{10pt} y’=3x^2-4\)
接点を\( \,(\,t\,,\,t^3-4t+2\,)\,\)とおくと、
求める接線は
\(\hspace{10pt} y-(t^3-4t+2)=(3t^2-4)(x-t)\) ･･･①
とおけます。
この形で表しておくことがポイントですよ。
これが原点 \((\,0\,,\,0\,)\) を通ることより、
\( (\,x\,,\,y\,)=(\,0\,,\,0\,)\) を①に代入すると
\(\begin{eqnarray} 0-(\,t^3-4t+2\,)\,&=&\,(\,3t^2-4\,)(\,0-t\,)\\
-t^3+4t-2&=&-3t^+4t\\
t^3&=&1
\end{eqnarray}\)
これを満たす実数は \(t=1\) だけです。
よって求める接線の方程式は①より、
\(\begin{eqnarray}\displaystyle
y-(\,1^3-4\cdot 1+2\,)&=&(\,3\cdot 1^2-4\,)(\,x-1\,)\\
y-(\,1-4+2\,)&=&(\,3-4\,)(\,x-1\,)\\
y-(-1)&=&-(\,x-1\,)
\end{eqnarray}\)
よって求める接線は
\( \underline{ y=-x }\)
概図を書いて接線のだいたいの傾きと本数を予測しておくと確認しやすいです。
ここでは接線が１本しかありませんでしたが、
３次関数に曲線上以外の点から接線を引く場合、２本または３本あることもあります。
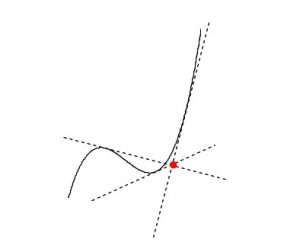
グラフで確認してみると分かります。
次は法線を求めて見ましょう。接線がわかれば簡単ですよ。
接線は積分（面積）ともは大きく関わってくるので大切なところです。