微分法と積分法の要点（数学Ⅱ）

微分法と積分法の数学Ⅱの範囲の要点のまとめページです。
微分法では導関数や接線の方程式、増減表やグラフ、
積分法においては面積や体積の求め方など重要なポイントがたくさんありますので確認しておいてください。

最近では文系の人にも数学\(Ⅲ\)が（大学で）必要とされる場面が多いですが、
ここでは数学\(\,Ⅱ\,\)の基礎的な範囲に限定してまとめておきます。
※
詳しく説明すると、微分法積分法は数学\(Ⅱ\)全体の半分の内容を占めます。
ここでは体積について（今のところ）触れていません。

微分法の要点

微分法から数学らしい\(\,？\,\)記号や表現が続々と出てきます。
用語の意味が分かっていないと通用しない分野でもあるので定義が大切になりますが、
数学\(\,Ⅱ\,\)における厳密性はそれほどありません。
何故なら、数学\(\,Ⅲ\,\)においても厳密にはやらないからです。笑
もちろん、意味を理解することは大切ですが、先ずは記号や用語に慣れてある程度使える様になりましょう。

微分係数

微分係数とは関数の変化率を細かく区切った極限値のことですが、
用語を2つ確認してから定義します。

平均変化率とは

\(\color{red}{\fbox{　平均変化率　}}\)

関数\(\,f(x)\,\)において、\(\,x\,\)が\(\,a\,\)から\(\,b\,\)まで変化するとき、
　\(\,x\,\)の変化量　\(\color{red}{b-a}\)　を\(\,x\,\)の増分
　\(\,y\,\)の変化量　\(\color{blue}{f(b)-f(a)}\)　を\(\,y\,\)の増分
といい、
　\(\hspace{10pt}\displaystyle \frac{　(\,yの増分)　}{　(\,xの増分)　}=\frac{\color{blue}{f(b)-f(a)}}{\color{red}{b-a}}\)
を、
　\(\,x\,\)が\(\,a\,\)から\(\,b\,\)まで変化するときの、
　関数\(\,y=f(x)\,\)の平均変化率
という。

※
異なる\(\,2\,\)点の変化の割合（直線の傾き）を難しそうにいっているだけです。

極限値とは

\(\color{red}{\fbox{　極限値　}}\)

関数\(\,f(x)\,\)において、
　\(\,x\,\)が限りなく\(\,a\,\)に近づくとき
　\(\,f(x)\,\)の値が一定値\(\,A\,\)に近づくなら、
この\(\,A\,\)を
　\(\,x\,\)が\(\,a\,\)に限りなく近づくときの極限値という。

極限値は
　「\(\,x\,\rightarrow \,a\,\)　のとき　\(\,f(x)\,\rightarrow \,A\,\)」
または、極限（limit）という英語を使って
　「\(\displaystyle \,\color{red}{\lim_{x \to a} f(x)=A}\,\)」
と表します。
この等号は\(\,A\,\)に限りなく近づくという意味ですが、
一致しても使い方には問題ありません。
※
長くなるので無視してください。笑

使い方は例題で見た方が早いです。

⇒　極限値の求め方（不定形を含む問題も数学Ⅱの範囲で解く方法）

極限値を詳しくやりたい場合だけ見ておいてください。

⇒　極限値とは（数学Ⅱ：収束と無限大への発散と不定形について）

不定形という言葉は出てきませんが数学\(Ⅲ\)を視野に入れているなら目を通しておきましょう。

⇒　極限の分数式の中にある係数を決定する問題の解き方

ちょっとした応用ですが数学\(Ⅱ\)でも出てきます。

微分係数の定義

\(\color{red}{\fbox{　微分係数の定義　}}\)

　関数\(\,y=f(x)\,\)の\(\,x=a\,\)における微分係数とは
　\(\hspace{10pt}\displaystyle \color{red}{f'(a)=\lim_{h \to 0}\frac{f(a+h)-f(a)}{h}}\)
のことである。

これは平均変化率
　\(\hspace{10pt}\displaystyle \frac{\color{blue}{f(b)-f(a)}}{\color{red}{b-a}}\)
において、\(\,x\,\)の増分を\(\,h\,\)とおくと
　\(\,b-a=h\,\)　なので　\(\,b=a+h\,\)
と置き換えた場合の\(\,h\,\rightarrow \,0\,\)の極限値です。

つまり、極めて小さな変化で見たときの平均変化率を表していて、
関数\(\,y=f(x)\,\)の\(\,x=a\,\)における接線の傾きを表しています。
「導関数」でも出てきますが、
　\(\,f(x)\,\)の\(\,x=a\,\)での微分係数は\(\,f'(a)\,\)
と表すことを忘れないでください。

微分係数と接線の傾き

\(\color{red}{\fbox{　接線の傾きと微分係数　}}\)

　関数\(\,y=f(x)\,\)の\(\,x=a\,\)での「微分係数\(\,f'(a)\,\)は」、
関数\(\,y=f(x)\,\)のグラフ上の
　「点\(\,(\,a\,,\,f(a)\,)\,\)における接線の傾き」
に等しい。

これは覚えておかないと微分積分は全滅といって良いです。笑

導関数と微分の計算

導関数と微分係数は何が違う？と感じる人もいるでしょう。

\(\,y=f(x)\,\)という関数から求める方法は同じですが、
　微分係数が「ある点の接線の傾き」で、
　導関数は「微分係数を全体でつなげた関数」、
とちょっとだけ見方が違う、と考えておけば良いです。

もう少し具体的にいうと、\(\,y=f(x)\,\)において
　\(\hspace{10pt}\,x=a\,,\,b\,,\,c\,,\,\cdots\,\)
と変化するときの微分係数を
　\(\hspace{10pt}f'(a)\,,\,f'(b)\,,\,f'(c)\,,\,\cdots \)
と対応させたときの関数を導関数といいます。

\(\color{red}{\fbox{　導関数の定義　}}\)

　関数\(\,y=f(x)\,\)の導関数とは
　\(\hspace{10pt}\displaystyle \color{red}{f'(x)=\lim_{h \to 0}\frac{f(x+h)-f(x)}{h}}\)
　で定められる関数である。

導関数を表す記号はいくつかありますが、\(\,y=f(x)\,\)において
　\(\displaystyle \,f'(x)\,,\,y’\,,\,\frac{dy}{dx}\,,\,\frac{d}{dx}f(x)\,\)
はすべて同じ意味です。

そして、\(\,f(x)\,\)の導関数\(\,f'(x)\,\)を求めることを「微分する」といいます。

\(\color{red}{\fbox{　微分の公式　}}\)

　\(\,c\,\)が定数のとき
　\(\hspace{10pt}\displaystyle (c)’=\frac{d}{dx}c=0\)

　\(\,m\,\)が正の定数のとき
　\(\hspace{10pt}\displaystyle (x^m)’=\frac{d}{dx}x^m=mx^{m-1}\)

証明は必要ないでしょう。
　定数は微分すると\(\,0\,\)になる。
　\(\,m\,\)次の関数は微分すると係数が\(\,m\,\)で次数が\(\,1\,\)小さくなる。
ということです。

例えば、（定数を微分すると\(\,0\,\)になるというのは良いとして）
　\(\,(x^3)’=3x^2\,,\,(x^5)’=5x^4\,\)

\(\,m\,\)は自然数でなくても成り立ちますが、
自然数の整関数の微分ができない高校生はいないと思いたい。笑

そして、関数の和と差において線型性があります。

\(\color{red}{\fbox{　微分の性質　}}\)

　\(\,y=kf(x)\,\)を微分すると　\(\,y’=kf'(x)\,\)
　\(\,y=f(x)+g(x)\,\)を微分すると　\(\,y’=f'(x)+g'(x)\,\)
　\(\,y=f(x)-g(x)\,\)を微分すると　\(\,y’=f'(x)-g'(x)\,\)

多項式の微分は、各項を微分して足したり引いたりして良いということです。

⇒　微分係数と導関数の定義および微分の公式

もう少していねいに説明してあります。笑

微分係数と接線の方程式

これは必ず覚えましょう。

\(\color{blue}{\fbox{　接線の傾きと微分係数（定理）　}}\)

　関数\(\,y=f(x)\,\)の\(\,x=a\,\)での微分係数\(\,f'(a)\,\)は、
　曲線\(\,y=f(x)\,\)上の点
　\(\hspace{10pt}\,(\,a\,,\,f(a)\,)\,\)での接線の傾き
　に等しい。

このことから接線の公式が導かれます。

\(\color{red}{\fbox{　接線の公式　}}\)

　　\(\,f'(a)\,\)が存在するとき、
　曲線\(\,y=f(x)\,\)上の点\(\,(\,a\,,\,f(a)\,)\,\)における接線は
　\(\hspace{10pt}\color{red}{y-f(a)=f'(a)(x-a)}\)
　で与えられる。

傾き\(\,m\,\)で\(\,(\,a\,,\,b\,)\,\)を通る直線は
　\(\,y-b=m(x-a)\,\)
であることをことある毎に強調しているのはこの接線のためです。

⇒　微分を使った接線の方程式の求め方（接点が曲線上にある場合と無い場合）

接線問題は大きく2つの場合がありますが、基本方針は1つです。

⇒　微分を使った接線に垂直な法線の方程式の求め方と公式

ついでに法線についても求められるようになっておきましょう。

さて、微分の有効的な使い方はここからです。

微分法で見る関数の値の変化

微分法による関数の増加、減少について詳しい説明は別にしますので、
ここでは簡単に、定義、定理だけまとめておきます。

関数の増減と極大値および極小値

\(\color{red}{\fbox{　関数の増加と減少（定義）　}}\)

　関数\(\,f(x)\,\)について、区間\(\,I\,\)に属する任意の\(\,x_1\,,\,x_2\,\)に対し、
\(　\color{red}{①　x_1\,＜\,x_2\,　⇔　\,f(x_1)\,＜\,f(x_2)}\,\)
　が成り立つとき、\(\,f(x)\,\)は区間\(\,I\,\)で増加である。
\(　\color{red}{②　x_1\,＜\,x_2\,　⇔　\,f(x_1)\,＞\,f(x_2)}\,\)
　が成り立つとき、\(\,f(x)\,\)は区間\(\,I\,\)で減少である。
という。

難しく考えなくて良いです。
左から見ていったときグラフが上に上がるとき増加、下に下がるとき減少、ということです。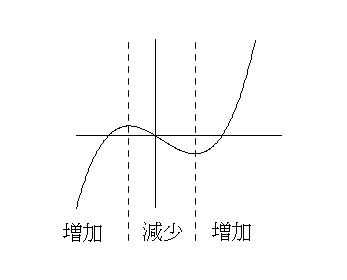次は定理ですが、区間について細かくいうと長くなるので、少し省略します。笑

\(\color{red}{\fbox{　微分係数の符号と増加減少（定理）　}}\)

　関数\(\,f(x)\,\)が、
　①　\(\,f'(x)\,＞\,0\,\)の区間では\(\,f(x)\,\)は増加する。
　②　\(\,f'(x)\,＜\,0\,\)の区間では\(\,f(x)\,\)は減少する。
※
\(\,f'(x)=0\,\)のときはその区間で定数ですが、連続であればどちらの区間に含めても良いです。

証明は数学\(\,Ⅲ\,\)でやってください。（「平均値の定理」利用）
増加するか減少するかは、
接線の傾きが正か負かに注目すればなんとなくでも理解できるでしょう。

\(\color{red}{\fbox{　極大値と極小値の定義　}}\)

関数\(\,f(x)\,\)が、
\(①　\,x=\alpha\,\)を境として「増加から減少に変化」するとき
　\(\hspace{10pt}「f(x)\,はx=\alpha\,で極大である」\)といい、
　\(\hspace{10pt}f(\alpha)を「極大値」\)という。
\(②　\,x=\beta\,\)を境として「減少から増加に変化」するとき
　\(\hspace{10pt}「f(x)\,はx=\beta\,で極小である」\)といい、
　\(\hspace{10pt}f(\beta)を「極小値」\)という。
また、極大値、極小値をまとめて極値という。
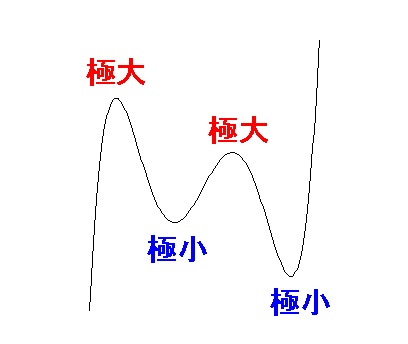これは連続であればなめらかでなくても言えます。
ただし、増加と減少が変化しなければ極値とはいいません。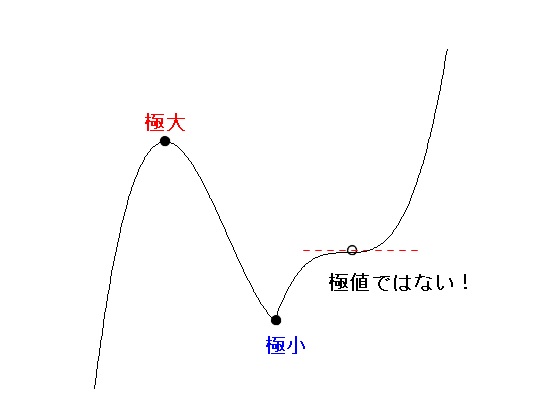

⇒　極値（極大値・極小値）を持つ条件と持たない条件

極値を持つ条件がわかりにくい場合は、定義をもう一度確認しておきましょう。

極値を探す手段は次の増減表です。

関数の増減表とグラフの応用

増減表は関数を見るときに最も大切な道具だと考えておいてください。
例えば、\(\,f(x)=x^3-3x\,\)の増減は
　\(\hspace{10pt} f'(x)=3x^2-3\,=3(x+1)(x-1)=0\,\)
から、\(\,x=-1\,,\,1\,\)を境に変化するので、
　\(\,\begin{array}{|c|c|c|c|c|c|}\hline
x & \cdots & -1 & \cdots & 1 & \cdots \\
\hline
f’(x) & + & 0 & – & 0 & + \\
\hline
f(x) & \nearrow & 2 & \searrow & -2 & \nearrow \\ \hline
\end{array}\,\)
となりますが、これを\(\,xy\,\)平面に書き込めばグラフができあがります。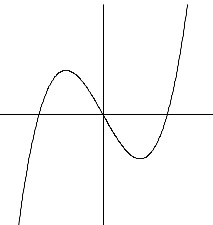

増減表の書き方

増減表の書き方は
　①　\(\,f'(x)\,\)を求める。
　②　\(\,f'(x)\,\)の正と負の区間を調べる。
これだけで良いのですが極大、極小を調べるには、
　\(\,f'(x)=0\,\)となる\(\,x\,\)を求める。
これだけで、数学\(\,Ⅱ\,\)の関数の増減は調べることができます。

⇒　増減表とグラフの書き方（関数の増加減少と極値）

グラフの書き方もまとめてありますので確認してください。

⇒　三角関数の最大値最小値問題を微分を使って解く方法（数学2）

グラフが描ければ方程式や不等式、最大値最小値に応用できます。

積分法の要点

数学\(\,Ⅱ\,\)の積分法では、簡単な多項式における面積を直感的にでもイメージできる範囲で求めることが目的になります。
積分そのものは微分の逆演算（逆の操作）なので難しいことはありません。

定義や定理は少ないですが、様々な関数や区間における問題に利用できます。
応用が効くということですが、定義と定理をしっかり覚えておけば使えます。
（高校生には迷惑な話でしょうか？笑笑）

積分は数学\(Ⅱ\)においても応用範囲が広いので、
後半に例題を多めに入れてありますので、基本定理を確認しながら見ておくと良いです。

不定積分

「不定積分」と「原始関数」は同じものだと考えて良いです。
概念を区別するほどの厳密な積分法は大学に進学してから学んでください。

不定積分の定義と定理（公式）

\(\color{red}{\fbox{　不定積分の定義　}}\)

　\(\,x\,\)の関数\(\,f(x)\,\)が与えられたとき、
微分すれば\(\,f(x)\,\)となる関数\(\,F(x)\,\)を\(\,f(x)\,\)の不定積分という。
つまり、
　\(\,F(x)\,\)は\(\,f(x)\,\)の不定積分　⇔　\(\,F'(x)=f(x)\,\)

\(\color{red}{\fbox{　不定積分の記号と積分定数　}}\)

　\(\,f(x)\,\)の不定積分の1つを\(\,F(x)\,\)とすると
　\(\hspace{10pt}\displaystyle \int f(x)dx=F(x)+C　(\,C\,は定数)\)
ここで、定数\(\,C\,\)を積分定数という。

不定積分の公式

　\(\color{red}{\fbox{　不定積分の公式(1)　}}\)

　\(\,n\,\)が\(\,0\,\)または正の整数の定数とすると
　\(\hspace{10pt}\displaystyle \color{red}{\int x^n dx=\frac{1}{n+1}x^{n+1}+C　（\,C\,は積分定数)}\)

※
\(\,n=0\,\)のときは\(\,x^0=1\,\)となるので\(\,a\,\)を定数とすると
　\(\hspace{10pt}\displaystyle \int a\,dx=ax+C　(\,C\,は積分定数)\)
となるということです。
定数\(\,n\,\)の範囲は拡張できますが、数学\(\,Ⅱ\,\)ではここまでで大丈夫です。

　\(\color{red}{\fbox{　不定積分の公式(2)　}}\)

　\(\,f(x)\,,\,g(x)\,\)が連続ならば、
　\(\hspace{10pt}\displaystyle \color{red}{\int kf(x)dx=k\int f(x)dx}\)
　\(\hspace{10pt}\displaystyle \color{red}{\int \{f(x)+g(x)\}dx=\int f(x)dx+\int g(x)dx}\)
　\(\hspace{10pt}\displaystyle \color{red}{\int \{f(x)-g(x)\}dx=\int f(x)dx-\int g(x)dx}\)
※
数学\(\,Ⅱ\,\)で積分するのは連続な関数だけなので、『連続ならば』というのは忘れて良いです。

この3つは書き換えると、
　\(\,F'(x)=f(x)\,,\,G'(x)=g(x)\,\) のとき
　\(\hspace{10pt}\displaystyle \int kf(x)dx\,=\,kF(x)+C　(\,k\,,\,C\,は定数)\)
　\(\hspace{10pt}\displaystyle \int \{f(x)+g(x)\}dx\,=\,F(x)+G(x)+C\)
　\(\hspace{10pt}\displaystyle \int \{f(x)-g(x)\}dx\,=\,F(x)-G(x)+C\)
と同じことです。
（もちろん\(\,C\,\)は「積分定数」）

⇒　不定積分（原始関数）の定義と公式と計算問題の解き方

いくつか練習すればすぐ慣れます。

定積分

数学\(\,Ⅱ\,\)の定積分は、形式上の「定積分の定義」で覚えていれば良いです。

定積分の定義

\(\color{red}{\fbox{　定積分の定義　}}\)

　\(F'(x)=f(x)\,\)のとき
　\(\hspace{10pt}\displaystyle \color{red}{\int_a^b f(x)dx=\left [F(x)\right ]_a^b=F(b)-F(a)}\)
　を関数\(\,f(x)\,\)の\(\,a\,\)から\(\,b\,\)までの定積分という。

これは面積を表しているのではない、ということは知っておきましょう。

定積分の公式

不定積分と同様に公式があります。

\(\color{red}{\fbox{　定積分の公式(1)　}}\)

　①\(\hspace{10pt}\displaystyle \color{red}{\int_a^b kf(x)dx=k\int_a^b f(x)dx　(\,k\,は定数)}\)
　②\(\hspace{10pt}\displaystyle \color{red}{\int_a^b \{f(x)+g(x)\}dx=\int_a^b f(x)dx+\int_a^b g(x)dx}\)
　③\(\hspace{10pt}\displaystyle \color{red}{\int_a^b \{f(x)-g(x)\}dx=\int_a^b f(x)dx-\int_a^b g(x)dx}\)

①は積分してから\(\,k\,\)（実数）倍しても良いと、
②③はまとめて積分しても良いし、それぞれの項を積分して足したり引いたりしても良い、ということです。
例題で見た方が早いでしょうから別ページの詳しい説明を見てください。

\(\color{red}{\fbox{　定積分の公式(2)　}}\)

　④\(\hspace{10pt}\displaystyle \color{red}{\int_a^a f(x)dx=0}\)
　⑤\(\hspace{10pt}\displaystyle \int_\color{blue}{b}^\color{red}{a} f(x)dx=\color{magenta}{-}\int_\color{red}{a}^\color{blue}{b }f(x)dx\)
　⑥\(\hspace{10pt}\displaystyle \color{red}{\int_a^b f(x)dx=-\int_a^cf(x)+\int_c^b f(x)dx}\)

④は積分区間の上端と下端が同じときは\(\,0\,\)になり、
⑤積分区間が逆転すると積分された値は符号が逆になるということです。
⑥は積分区間を分けても良いということです。

\(\color{red}{\fbox{　偶関数、奇関数の定積分　}}\)

①　\(\,f(x)\,\)が偶関数なら\(\,\displaystyle \int_{-a}^a f(x)dx=2\int_0^a f(x)dx\)
②　\(\,f(x)\,\)が奇関数なら\(\,\displaystyle \int_{-a}^a f(x)dx=0\)

偶関数、奇関数のグラフから考えれば明らかな公式です。

\(\color{red}{\fbox{　微分積分学の基本定理　}}\)

　\(\,a\,\)を定数とすると
　\(\hspace{10pt}x\,\)の関数\(\displaystyle \,\int_a^x f(t)dt\,\)\,\)の導関数は\(\,f(x)\,\)となる。
　\(\hspace{10pt}\displaystyle \color{red}{\frac{d}{dx}\int_a^x f(t)dt=f(x)}\)

この定理は何で微分し、何で積分するかを見れば明らかです。
関数の形が同じであれば文字は違っても定積分の結果は同じだということです。

　\(\hspace{10pt}\displaystyle \color{blue}{\int_a^b f(t)dt=\int_a^b f(x)dx}\)

⇒　数学2（整関数）の定積分の公式（定義と定理と計算問題で使える公式）

定積分を例題を入れてまとめてあります。

積分と図形の面積の関係

定積分は積分する変数から見れば定数にはなりますが、
　定積分が必ず面積を表すとは限らない
ということは忘れないでください。

定積分で面積を求める公式

\(\color{red}{\fbox{　定積分と面積(1)　}}\)

　\(\,a\,≦\,x\,≦\,b\,\)において\(\,\color{red}{f(x)\,≧\,0}\,\)のとき、
　\(\,y=f(x)\,\)のグラフと\(\,x\,\)軸と、
　\(\,2\,\)直線\(\,x=a\,,\,x=b\,\)で囲まれる面積\(\,S\,\)は
　\(\hspace{10pt}\displaystyle \color{red}{S=\int_a^b f(x)dx}\)
　となる。

\(\color{red}{\fbox{　定積分と面積(2)　}}\)

　\(\,a\,≦\,x\,≦\,b\,\)において\(\,\color{blue}{f(x)\,≦\,0}\,\)のとき、
　\(\,y=f(x)\,\)のグラフと\(\,x\,\)軸と、
　\(\,2\,\)直線\(\,x=a\,,\,x=b\,\)で囲まれる面積\(\,S\,\)は
　\(\hspace{10pt}\displaystyle \color{blue}{S}=\int_a^b \{-f(x)\}dx=\color{blue}{-\int_a^b f(x)dx}\)
　となる。

これは\(\,x\,\)軸を\(\,y=0\,\)の曲線（直線）と考えています。
一般化しておきます。

\(\color{red}{\fbox{　定積分と面積(3)　}}\)

　　\(\,a\,≦\,x\,≦\,b\,\)において\(\,\color{red}{f(x)\,≧\,g(x)}\,\)のとき、
　\(\,y=f(x)\,\)と\(\,y=g(x)\,\)のグラフと、
　\(\,2\,\)直線\(\,x=a\,,\,x=b\,\)で囲まれる面積\(\,S\,\)は
　\(\hspace{10pt}\displaystyle S=\int_a^b \{f(x)-g(x)\}dx\)
　となる。

グラフが上になる曲線から下になる曲線を引いてその区間で積分すれば面積になるということです。

※
面積を求める問題はこの上下関係を見極めることがポイントです。

⇒　整関数の定積分の計算問題の解き方

定積分を面積問題も例題を含めて確認してください。

定積分と方程式を利用する場合

⇒　定積分で積分区間の文字（定数）を求める問題の解き方

微分積分の基本定理を利用する場合

⇒　定積分を関数と見るときの極値と定数を求める問題の解き方

絶対値がついた関数の定積分も含んだ問題

⇒　定積分によって面積を求める問題の解き方と公式

面積を求めるときの大切なポイントを接線を含めて説明しています。

⇒　２本の接線と曲線で囲まれる面積の求め方（定積分）