整関数での定積分の定義と定理(公式)をまとめておきます。
数学Ⅱでは整関数だけを考えれば良いので意味さえ理解できて、微分ができれば問題ありません。
ただ、定積分は面積を意味しているのではありませんので注意してください。
定積分まで来るとさまざまな問題があるのでそれぞれを別に取り上げて説明しますが、ここでは不定積分と定積分の違いだけでも見ておいてください。
整関数の定積分の定義
あまりむずかしく考えなくて良いですが、
整関数における定積分と不定積分の違いを定義を加えて説明しておきます。
【定義】(定積分の定義と記号)
\(\,F(x)\,\)が区間\(\,a\,≦\,x\,≦\,b\,\)連続な関数\(\,f(x)\,\)の不定積分のとき、
\(\hspace{10pt} \displaystyle \int_a^b f(x)\,dx=\left[F(x)\right]_a^b=F(b)-F(a)\)
のことを、
\( f(x)\) の \( a\) から \(b\) までの定積分という。
「連続な関数」というのは切れ目のない関数ということですが、
整関数をあつかう数学\(\,Ⅱ\,\)ではほとんど考えなくて良いです。
不定積分と定積分の違い
不定積分との違いは、
「積分区間がある」
ことと、計算結果が
「関数ではなく値」
であることです。
この「値」は面積ではありませんので注意が必要です。
後で説明を加えます。
例えば、
不定積分の場合 積分定数 \( C\) を用いると
\(\hspace{10pt} \displaystyle \int 2xdx=x^2+C\)
と関数で求まります。
定積分では
\(\hspace{10pt} \displaystyle \int_1^3 2x\,dx=\left[x^2\right]_1^3\,=3^2-1^2\,=8\)
と値で結果が出ます。
定積分 \( \displaystyle \int_a^b f(x)\,dx\) において、
\(\,f(x)\,\)を「被積分関数」
といい、
\(\,a\,\)を「下端(かたん)」
\( \,b\,\)を「上端(じょうたん)」
といいます。
積分する \(x\) を「積分変数」、
\( a\,≦\,x\,≦\,b\) を「積分区間」といいます。
説明するとややこしくなるので省略しますが、
積分区間は上端と下端の大小に限定はありません。
ところで、簡単にいえば
「定積分は不定積分の区間付き積分」
です。
不定積分は積分定数が無限にあったはずなのですが定積分はどうして値が定まるのか?
と疑問になるかもしれないのでちょっとだけ説明しておきます。
例えばですが、
\( f(x)=2x\,\)の不定積分(原始関数)は\(\,C\,\)を定数として
\( F(x)=x^2\) や \( F(x)=x^2+C\)
があります。
被積分関数を \( f(x)\)、
積分区間を \( 1\,≦\,x\,≦\,2\)
とすると、
\( \displaystyle \int_1^2 2x\,dx=\left[x^2\right]_1^2\,=(2^2)-(1^2)=3\)
\( \displaystyle \int_1^2 2x\,dx=\left[x^2+C\right]_1^2\,=(2^2+C)-(1^2+C)=3\)
のように不定積分の定数は関係なく同じ値になります。
どの不定積分を使っても間違いではありませんが、
できるだけ簡単な(計算しやすい)不定積分を使って計算すれば良いのです。
定積分の定理
すべて連続な関数であるということを前提として定理を並べておきます。
普通に使って良いことなので納得したら先に進んで下さいね。
不定積分のときに成り立っていた線型性は定積分においても成り立ちます。
【定理】
ⅰ) \( \displaystyle \int_a^b kf(x)dx=k\int_a^b f(x)dx\)
( \( k\) は定数とする。)
ⅱ) \( \displaystyle \int_a^b \left\{f(x)+g(x)\right\}dx\displaystyle =\int_a^b f(x)dx + \int_a^b g(x)dx\)
ⅲ) \( \displaystyle \int_a^b \left\{f(x)-g(x)\right\}dx\displaystyle =\int_a^b f(x)dx – \int_a^b g(x)dx\)
普通に定積分すればいつも使っていることなので気にする必要はありません。
この手の練習問題も別のところで追加しますが、
例えば、
\( \displaystyle \int_1^2 (2x+4)dx\)
を計算するとき
\(\hspace{10pt} \displaystyle \int_1^2 (2x+4)dx\\
\displaystyle =\left[x^2+4x\right]_1^3\\
=(3^2+4\cdot3)-(1^2+4\cdot 1)\\
=(9+12)-(1+4)\\
=21-5\,=16\)
としても
\(\hspace{10pt} \displaystyle \int_1^2 (2x+4)dx\\
\displaystyle =\underline{2\int_1^2 x\, dx + \int_1^2 4\,dx} \\
\displaystyle =\left[x^2\right]_1^3 + \left[4x\right]_1^3\\
=(3^2-1^1)+(4\cdot3- 4\cdot 1)\\
=(9-1)+(12-4)=8+8=16\)
としても良いですよ、ということです。
この例えは余計ややこしくしているのは分かると思いますが、
\(\hspace{10pt}\displaystyle \int_1^2 (3x^2+2x+4)dx\, – \,\int_1^2 (3x^2-2x+4)dx \)
のように積分区間が同じときは、
\(\hspace{10pt} \displaystyle \int_1^2 \underline{(\color{red}{3x^2+2x+4})}dx \,-\, \int_1^2 \underline{(\color{blue}{3x^2-2x+4})}dx \\
\displaystyle =\int_1^2 \left\{\underline{\color{red}{(3x^2+2x+4}) \,-\, (\color{blue}{3x^2-2x+4})}\right\}dx\\
\displaystyle =\int_1^2 (3x^2+2x+4-3x^2+2x-4)dx\\
\displaystyle =\int_1^2 4x\,dx\\
\displaystyle =\left[2x^2\right]_1^2\\
=(2\cdot 2^2)-(2\cdot 1^2)=8-2\,=6\)
のように被積分関数が簡単になることが多いので多いに利用して下さい。
積分区間の定理
積分区間の定理ついては、面積と定積分との関係をみながら進めた方が分かり易いので後で詳しく説明します。
ここでは、定理の紹介程度で先に進みます。
【定理】(積分区間に関する性質)
ⅰ) \( \displaystyle \int_a^a f(x)dx=0\)
ⅱ) \( \displaystyle \int_a^b f(x)dx=-\int_b^a f(x)dx\)
ⅲ) \( \displaystyle \int_a^c f(x)dx\displaystyle =\int_a^b f(x)dx + \int_b^c f(x)dx \)
ⅰ)は上端と下端が同じで、
「積分区間がない」
と考えてください。
ⅱ)は上端と下端が逆で、
「定積分を逆にすることで符号が変わる」
ことを確認しておけば大丈夫です。
\(\hspace{10pt} \displaystyle \int_a^b f(x)dx\\
\displaystyle =\left[F(x)\right]_a^b\\
=F(b)-F(a)\\
=-(F(a)-F(b))\\
\displaystyle =-\int_b^a f(x)dx\)
ⅲ)は被積分関数が違う場合に積分区間を分けるとき役に立つものです。
絶対値の関数などで良く使います。
\(\hspace{10pt} \displaystyle \int_{-1}^{1} |x| \,dx\\
\displaystyle =\int_{-1}^{0} (-x) \,dx +\int_{0}^{1} (x)\,dx\)
いずれにしてもいくつか具体的に関数を見ながら例題を解けばすぐに分かることです。
例題は別のところに追加して行きます。
偶関数と奇関数の定積分
偶関数と奇関数については整関数を見る時は簡単です。
\(\,x\,\)の関数で、
\(\,x\,\)の指数が偶数だけの関数のときを偶関数、
\(\,x\,\)の指数が奇数だけの関数のときを奇関数、
といいます。
グラフの特長などは後で説明しますが、先に定義を書いておきます。
【定義】(偶関数と奇関数の定義)
ⅰ)定義域内にある任意の \( x\) に対し、
\(\hspace{10pt} f(-x)=f(x)\)
が成り立つ関数\(\, f(x)\,\)を偶関数という。
ⅱ)定義域内にある任意の\(\,x\,\)に対し、
\(\hspace{10pt} f(-x)=-f(x)\)
が成り立つ関数\(\, f(x)\,\)を奇関数という。
例えば、
\(\hspace{10pt} f(x)=x^4-3x^2+1\)
これはすべての項の指数が偶数になっているので偶関数です。
(定数項は「0次」の項です。)
もちろん、項が1つの場合も同じですよ。
\(\hspace{10pt} f(x)=x^3+x\)
これはすべての項の指数が奇数になっているので奇関数です。
グラフの特長は、
偶関数は \( f(-x)=f(x)\) が成り立つので、
\( \color{red}{y}\) 軸に対して対称なグラフになります。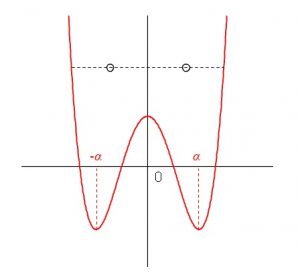
奇関数は \( f(-x)=-f(x)\) が成り立つので、
原点に関して対称なグラフになります。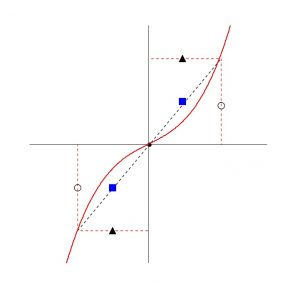
グラフの特長と合わせて考えたいのが偶関数、奇関数についての定積分の性質です。
【定理】(偶関数と奇関数の定積分)
ⅰ) \( f(x)\) が偶関数なら
\(\hspace{10pt} \displaystyle \int_{\color{red}{-a}}^{a} f(x)dx=\color{red}{2}\int_\color{red}{0}^a f(x)dx\)
ⅱ) \( f(x)\) が奇関数なら
\( \displaystyle \int_{\color{red}{-a}}^{\color{red}{a}} f(x)dx=\color{red}{0}\)
ⅰ)は偶関数でグラフが\(\,y\,\)軸対称なので、
積分区間が
\(\,-a\,≦\,x\,≦\,0\,\)と\(\,0\,≦\,x\,≦\,a\,\)で定積分の値が同じ
になることをイメージすれば分かるでしょう。
もちろん、実際に定積分しても証明はできます。
\(\hspace{10pt} \displaystyle \int_{-a}^{a} x^{2n}dx\\
\displaystyle =\int_{-a}^0 x^{2n}dx + \int_{0}^a x^{2n}dx \\
\displaystyle =\int_{0}^a \{(-x)^2\}^n \,dx + \int_{0}^a x^{2n}\,dx \\
\displaystyle =\int_{0}^a x^{2n}dx +\int_{0}^a x^{2n}dx \\
\displaystyle =2\int_{0}^a x^{2n}dx \)
ⅱ)は奇関数の場合、
ⅰ)とは逆に原点対象なので定積分の値の符号が逆になるので「0」になります。
これも単項式でも成り立つ定理なので、線型性と合わせて考えると積分区間が
\( -a\, ≦ \,x\, ≦ \,a\)
のように下端と上端の絶対値が同じときは計算が楽になることがあり、良く使う定理です。
例
\(\hspace{10pt} \displaystyle \int_{-1}^{1} (3x^5+5x^4+7x^3+3x^2+9x+1)dx\\
\displaystyle = \int_{-1}^{1} (5x^4+3x^2+1)dx\\
\displaystyle = 2\int_{0}^{1} (5x^4+3x^2+1)dx\\
=2\left[x^5+x^3+x\right]_0^1\,=\,2(1+1+1)=6\)
奇関数部分は消えて、偶関数部分は積分区間を楽に計算できる範囲に分けることができました。
微分積分法の基本定理
この定理は定積分において積分区間の上端が変数\(\,x\,\)のとき、
積分変数が\(\,t\,\)であっても定積分が\(\,x\,\)の関数になるという高校生が苦手にしているものの1つです。
【定理】微分積分学の基本定理
\( \displaystyle \frac{d}{dx}\int_{a}^x f(t)dt=f(x)\)
積分するときは\(\,t\,\)の関数として\(\,x\,\)を定数扱いしますが、
その後\(\,x\,\)の関数とみて\(\,x\,\)で微分しています。
証明は\(\,f(x)\,\)の不定積分の1つを\(\,F(x)\,\)とすると、
\(\,F'(x)=f(x)\,\)なので
\( \displaystyle G(x)\displaystyle =\int_{a}^x f(t)dt=F(x)-F(a)\)
これを微分することで \( G'(x)=f(x)\) を示せます。
しかし、この証明は後でもいいので変数が変わることを見ておいてください。
定積分と面積に関する定理と公式
実は、定積分を利用した面積を求めることについての基本的な定理は1つだけです。
【定理】
区間 \( a ≦ x ≦ b\) で \( f(x)≧ 0\) であり、
\( f(x)\) が連続なら定積分
\( \displaystyle I\displaystyle =\int_a^b f(x)\)
の値は、
曲線 \( y=f(x)\) と \( x\) 軸
直線 \( x=a\) , \( x=b\)
によって囲まれる部分の面積 \( S\) に等しい。
ポイントは \( f(x)≧ 0\) としているところです。
マイナスのときは面積計算できませんので「囲まれた面積」という場合はそのまま計算することはできません。
定積分は \( f(x)\) の正負に関係なく計算できますが、面積計算ではできません。
これが定積分が面積ではないという理由です。
この定理に沿って面積は求めることになるので、
「関数を\(\,x\,\)軸より上に折り返す」
または、
「2つの曲線があれば上の曲線から下の曲線を引いて積分する」
というだけで面積は求めることができるのです。
数学\(\,Ⅱ\,\)であつかう関数は整関数の3次式までがほとんどなので、
いくつか覚えておくと便利な計算公式がありますが、
例題を解きながら納得した方がいいので練習問題は別のところでやることにします。
積分区間を分けることさえしっかりできれば、
面積を求めることは難しい計算ではありませんよ。
ここに載せたことは教科書にある定義や定理ですが、
これを書いておかないと先の説明が飛躍するので書いておきました。
定積分の前に不定積分の復習は欠かさないで下さい。
厳密な話はなしにして、不定積分があって定積分です。
ここまでが定積分の定理だということを念頭に例題に入りましょう。
これ以上の定義や定理は必要ありませんので安心して先に進みましょう。
数学\(\,Ⅱ\,\)の微分積分で必要なことはほとんどまとめてありますので総復習に利用してください。