数学Ⅱであつかう整関数の定積分の基本計算問題の解き方です。
微分積分となると総合的になってきますので問題の形はいろいろありますが、定積分を行うことにかわりはありません。
いろいろな技を使うよりも、基本通り解くことが得点力を安定させてくれる近道ですよ。
試験時間を考えると、定理を使って計算を工夫し時間の短縮はすべきですけどね。
定積分の計算問題
整関数の定積分ができるようになれば十分です。
定積分は不定積分に積分区間がついているだけなので、数学Ⅱの定積分は機械的に処理できますよ。
使うのは \( f(x)\) の不定積分を \( F(x)\) として
\( \displaystyle \int_a^b f(x)dx=F(b)-F(a)\)
だけです。
あれこれパターンを取り上げてたらキリありませんので、「置換積分」を見すえた問題はここでは取り上げません。
次の定積分を求めよ。
(1) \( \displaystyle \int_{-1}^3 (x^3-4x^2+3)dx\)
(2) \( \displaystyle \int_{-1}^2 (x+1)(x-2)dx\)
各項に
\( \displaystyle \int x^n=\frac{1}{n+1}x^{n+1}+C\)
を利用しますが、定積分では積分定数は計算しやすいもの「0」を選ぶのが普通です。
※
定積分では積分定数は何をとっても結果は同じになるので、できるだけ計算しやすい「0」を選んで良いということです。
(1)
\(\hspace{10pt} \displaystyle \int_{-1}^3 (x^3-4x^2+3)dx\\ \\
\displaystyle =\left[\frac{1}{4}x^4-\frac{4}{3}x^3+3x\right]_{-1}^{3}\\ \\
\displaystyle =\frac{1}{4}\{3^4-(-1)^4\}-\frac{4}{3}\{3^3-(-1)^3\}+3\{3-(-1)\}\\ \\
\displaystyle =\frac{1}{4}(81-1)-\frac{4}{3}(27+1)+3(3+1)\\ \\
\displaystyle =\frac{1}{4}(80)-\frac{4}{3}(28)+3(4)\\ \\
\displaystyle =20-\frac{112}{3}+12\\ \\
\displaystyle =\frac{60-112+36}{3}=\frac{-16}{3}=-\frac{16}{3}\)
3行目の計算を各項ごとに上端と下端の差を計算しています。
それを
\(\hspace{10pt} \displaystyle \int_{-1}^3 (x^3-4x^2+3)dx\\ \\
\displaystyle =\left[\frac{1}{4}x^4-\frac{4}{3}x^3+3x\right]_{-1}^{3}\\ \\
\displaystyle =\left\{ \frac{1}{4}(3)^4-\frac{4}{3}(3)^3+3(3)\right\}-\left\{ \frac{1}{4}(-1)^4-\frac{4}{3}(-1)^3+3(-1)\right\}\\ \\
\displaystyle =\left( \frac{1}{4}\cdot 81-4\cdot 3^2+9\right)-\left( \frac{1}{4}+\frac{4}{3}-3\right)\\ \\
\displaystyle =\frac{1}{4}\cdot 81-36+9- \frac{1}{4}-\frac{4}{3}+3\\ \\
\displaystyle =20-36+9-\frac{4}{3}+3\\ \\
\displaystyle =-4-\frac{4}{3}=-\frac{16}{3}\)
と先ず上端に専念して、その後下端に専念して、としてもかまいません。
項ごとに計算するメリットはありますけどね。
(2)普通に展開して積分しましょう。
\(\hspace{10pt} \displaystyle \int_{-1}^2 (x+1)(x-2)dx\\ \\
\displaystyle =\int_{-1}^2 (x^2-x-2)dx\\ \\
\displaystyle=\left[\, \frac{1}{3}x^3- \frac{1}{2}x^2-2x\,\right]_{-1}^2\\ \\
\displaystyle= \frac{1}{3}\{(2)^3-(-1)^3\}- \frac{1}{2}\{(2)^2-(-1)^2\}-2\{(2)-(-1)\}\\ \\
\displaystyle= \frac{1}{3}\cdot 9- \frac{1}{2}\cdot 3-2\cdot 3\\ \\
\displaystyle=3- \frac{3}{2}-6=\frac{6-3-12}{2}=-\frac{9}{2} \)
面積計算で便利な公式
ここでひとつよく知られた公式を紹介しておきます。
\( \displaystyle \color{red}{\int_{\alpha}^{\beta} (x-\alpha)(x-\beta)dx=-\frac{1}{6}(\beta-\alpha)^3}\)
これは2次方程式 \( ax^2+bx+c=0\) の2解を、
\( \alpha \,,\,\beta (\alpha \,< \,\beta)\) としたとき、
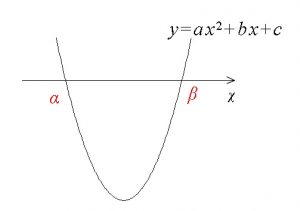
\( y=ax^2+bx+c\) と \( x\) 軸とで囲まれた面積は
\(\hspace{10pt} \displaystyle \int_{\alpha}^{\beta}(ax^2+bx+c)dx\\ \\
=a(x-\alpha)(x-\beta)dx\\ \\
=\displaystyle \frac{|a|}{6}(\beta-\alpha)^3\)
となるという面積問題の場面で良く使われます。
これは \(x\) 軸だけじゃなくて、放物線と直線の交点が \( \alpha \,,\,\beta\) の場合にも囲む面積として使える公式です。
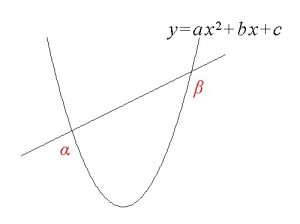
この公式は後々も使いますから記憶しておいて下さい。
ただし、
\( \displaystyle \int_{\alpha}^{\beta} (x-\alpha)(x-\beta)dx=-\displaystyle \frac{1}{6}(\beta-\alpha)^3\)
自体の値は「負(マイナス)」で面積を表しているのではありませんよ。
難しいことはいいません。
面積にしたかったら絶対値をつけて「正の値」にかえれば良いのです。
この公式を使う求積問題は、3次関数のときも似たような公式がありますので追加して説明することにします。
ところで、
\( \displaystyle \int_{-1}^2 (x+1)(x-2)dx\)
は公式そのものなので、
\(\hspace{10pt}\displaystyle \int_{-1}^2 (x+1)(x-2)dx\\ \\
\displaystyle =-\frac{1}{6}\{2-(-1)\}^3\\ \\
\displaystyle =-\frac{1}{6}\cdot 3^3=-\frac{27}{6}=-\frac{9}{2}\)
としても良いですよ。
ただし、不定積分から定積分が計算できるようにはなっておきましょう。
次も良く出てくる計算問題です。
定理により簡単になる積分計算
次の定積分を求めよ。
(1) \( \displaystyle \int_{-2}^2 x^3(x^2+3x+1)^2\,dx\)
(2) \( \displaystyle \int_{-1}^1 15x^2(x+1)^3\,dx\)
この形の問題が多いというのは、
積分区間の「下端」と「上端」が同じ
というところです。
被積分関数 \(f(x)\) が
奇関数なら
\(\hspace{10pt} \displaystyle \color{red}{\int_{-a}^{a} f(x)dx=0}\)
偶関数なら
\(\hspace{10pt} \displaystyle \color{red}{\int_{-a}^{a} f(x)dx =2\int_{0}^{a} f(x)dx }\)
つまり、整関数の場合
\(\hspace{10pt} \displaystyle \color{red}{\int_{-a}^{a} x^{2n-1}\,dx =0}\)
\(\hspace{10pt} \displaystyle \color{red}{\int_{-a}^{a} x^{2n} \,dx= 2\int_{0}^{a} x^{2n}\, dx}\)
になるということを利用すると計算が楽になります。
上端と下端が同じときは、
指数が奇数の部分の項は計算しなくてよく、
指数が偶数の部分は計算しやすい部分を2倍すれば良い、
ということに気をつけて計算しましょう。
(1)
\(\hspace{10pt} \displaystyle \int_{-2}^2 x^3(x^2+1)^2\,dx\\ \\
\displaystyle =\int_{-2}^2 x^3(x^4+2x^2+1)\,dx\\ \\
\displaystyle =\int_{-2}^2 (x^7+2x^5+x^3)\,dx=0\)
指数が奇数の項の和(奇関数の和)になっているので計算する必要がありません。
(2)
\(\hspace{10pt} \displaystyle \int_{-}^1 5x^2(x+1)^3\,dx\\ \\
\displaystyle =\int_{-1}^1 5x^2 ( x^3+3x^2+3x+1) \,dx\\ \\
\displaystyle =\int_{-1}^1 (5x^5+15x^4+15x^3+5x^2) \,dx\\ \\
\displaystyle =\int_{-1}^1 (5x^5+15x^3) \,dx + \int_{-1}^1 (15x^4+5x^2) \,dx\)
のように奇関数の部分と偶関数の部分とを分けると、奇関数の部分は計算しなくていいので、
\(\hspace{10pt} \displaystyle \int_{-1}^1 5x^2(x+1)^3\,dx\\ \\
\displaystyle =\int_{-1}^1 (5x^5+15x^4+15x^3+5x^2) \,dx\\ \\
\displaystyle =\int_{-1}^1 (15x^4+5x^2) \,dx\\ \\
\displaystyle =2\int_{0}^1 (15x^4+5x^2) \,dx\\ \\
\displaystyle =2\left[3x^5+\frac{5}{3}x^3\right]_{0}^{1}\\ \\
\displaystyle =2\left(3+\frac{5}{3}\right)=2\cdot \frac{14}{3}=\frac{28}{3}\)
整関数の積分計算は難しい計算がある訳ではありませんが、時間のかかるものが多いので要領よく、しなくて良い計算は省くことがポイントです。
特に、時間との戦いとなる試験では大切なことですよ。
文字決定問題はどの分野でも出てきます。
積分も例外ではありませんが難しくはありません。
使い方によっては微分法と積分法は他の分野でも大いに活躍できます。
