2019年(平成31年)度に行われたセンター試験数学1Aの問2の解説です。
第2問は三角比、図形の計量とデータの活用の問題があります。
資料の活用は例年通りのページ数の多さに嫌になるかもしれませんが、今年は優しい誘導付きです。
正解はセンターが発表していますので確認してください。
この問題は数学\(ⅠA\)のみの部分掲載となります。
センター試験2019年度数学1Aの第2問〔1〕三角比(図形の計量)
例年通り選択問題に平面幾何の項目があるのでここは得点しやすかったでしょう。
最初の条件は△ABCにおいて
\(\,\mathrm{AB=3}\,\)
\(\,\mathrm{BC=4}\,\)
\(\,\mathrm{AC=2}\,\)
だけです。
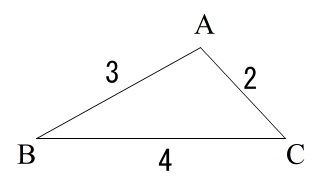
問題用紙に大きくスペースをくれています。
計算スペースでもありますが、図示するスペースですよ。
計算はたいしたことないので次のページの問題を一緒にしても良いのに、明らかに図を書いて考えなさい、といってくれているようなものです。
最後の年だからはっきり言うけど、センター試験では分野の融合がされないので各分野で使う定理などをあらかじめ予測しておくことができます。
(共通テストも形式が少し変わりますが内容は同じですよ。)
三角比だと
正弦定理
\(\displaystyle \frac{a}{\sin \mathrm{A}}=\frac{b}{\sin \mathrm{B}}=\frac{c}{\sin \mathrm{C}}=2R\)
余弦定理
\(a^2=b^2+c^2-2bc\cos \mathrm{A}\)
\(b^2=c^2+a^2-2ca\cos \mathrm{B}\)
\(c^2=a^2+b^2-2ac\cos \mathrm{C}\)
面積の公式
\(\begin{eqnarray}\displaystyle
S&=&\frac{1}{2}ab\sin \mathrm{C}\\
&=&\frac{1}{2}bc\sin \mathrm{A}\\
&=&\frac{1}{2}ca\sin \mathrm{B}
\end{eqnarray}\)
これを外して問題は作れないでしょう。笑
「\(\displaystyle \cos ∠\mathrm{BAC}=\frac{\color{black}{\fbox{\( アイ \)}}}{\color{black}{\fbox{\( ウ \)}}}\)であり、」
余弦(\(\,\cos\,\))について聞かれているので余弦定理です。
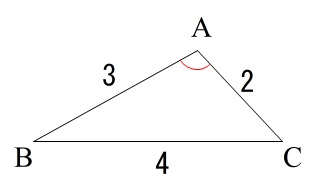
\(\begin{eqnarray} \displaystyle
\cos ∠\mathrm{BAC}&=&\frac{2^2+3^2-4^2}{2\times 2\times 3}\\
&=&\frac{4+9-16}{2\times 2\times 3}\\
&=&\frac{-3}{2\times 2\times 3}\\
&=&\frac{\color{black}{\fbox{\(\,\color{red}{ -1 }\,\)}}}{\color{black}{\fbox{\(\,\color{red}{ 4 }\,\)}}}
\end{eqnarray}\)
余弦定理を
\(\,a^2=b^2+c^2-2bc\cos \mathrm{A}\,\)
の形でしか覚えていない人は、代入して等式を解いてもそれほど時間は変わりませんのでかまいませんよ。
\(\cos ∠\mathrm{BAC}<0\) なので\(\,\mathrm{∠BAC}\,\)は\(\color{black}{\fbox{\( \color{red}{鈍角} \)}}\)です。
\(\color{red}{\sin^2 \theta+\cos^2 \theta=1}\)
なので
\(\begin{eqnarray} \displaystyle
\sin^2 ∠\mathrm{BAC}&=&1-\cos^2∠\mathrm{BAC}\\
&=&1-\left(-\frac{1}{4}\right)^2\\
&=&1-\frac{1}{16}\\
&=&\frac{15}{16}
\end{eqnarray}\)
三角形の内角においては正弦(\(\,\sin\,\))の値は正なので
\(\begin{eqnarray} \displaystyle
\sin ∠\mathrm{BAC}&=&\sqrt{\frac{15}{16}}\\
&=&\frac{\sqrt{\color{black}{\fbox{\(\color{red}{ 15 }\)}}}}{\color{black}{\fbox{\(\color{red}{ 4 }\)}}}
\end{eqnarray}\)
ここで条件が加わります。
「線分\(\,\mathrm{AC}\,\)の垂直二等分線と直線\(\,\mathrm{AB}\,\)の交点を\(\,\mathrm{D}\,\)」
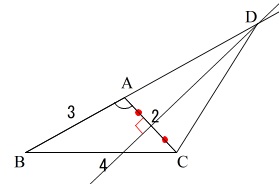
問題の誘導に乗ると
「\(\displaystyle \cos ∠\mathrm{CAD}=\frac{\color{black}{\fbox{\( ク \)}}}{\color{black}{\fbox{\( ケ \)}}}\)」
を求めることになりますが余弦の定義に戻ります。
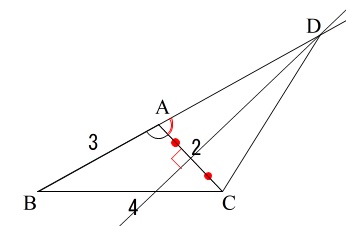
\(\begin{eqnarray}\displaystyle
\cos ∠\mathrm{CAD}&=&\cos (180^{\circ}-∠\mathrm{BAC})\\
&=&-\cos ∠\mathrm{BAC}\\
&=&\frac{\color{black}{\fbox{\(\,\color{red}{ 1 }\,\)}}}{\color{black}{\fbox{\(\,\color{red}{ 4 }\,\)}}}
\end{eqnarray}\)
誘導してくれているので\(\cos ∠\mathrm{BAC}\)はすでに求めていることは忘れないようにしましょう。
また、この垂直二等分線と\(\,\mathrm{AC}\,\)との交点を\(\,\mathrm{E}\,\)とすると
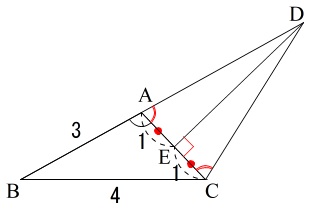
\(\,\mathrm{E}\,\)は線分\(\,\mathrm{AC}\,\)の中点で \(\,\mathrm{AE=1}\,\)
であり、余弦の定義から
\(\displaystyle \cos ∠\mathrm{DAE}=\frac{\mathrm{AE}}{\mathrm{AD}}\)
なので
\(\displaystyle \frac{1}{4}=\frac{1}{\mathrm{AD}}\)
から
\(\,\mathrm{AD}=\color{black}{\fbox{\(\,\color{red}{ 4 }\,\)}}\,\)
後は2つの三角形の面積の和を求めれば良いだけです。
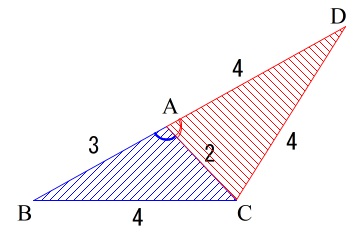
\(\sin (180^{\circ}-A)=\sin A\)
であることから
\(\displaystyle \sin ∠\mathrm{\color{blue}{BAC}}=\sin ∠\mathrm{\color{red}{DAC}}=\frac{\sqrt{15}}{4}\)
なので
\(\begin{eqnarray}\displaystyle
△\mathrm{DBC}&=&△\mathrm{BAC}+△\mathrm{CAD}\\
&=&\frac{1}{2}\cdot \mathrm{AB}\cdot \mathrm{AC}\cdot \sin ∠\mathrm{BAC}+\frac{1}{2}\cdot \mathrm{AC}\cdot \mathrm{AD}\cdot \sin ∠\mathrm{DAC}\\
&=&\frac{1}{2}\times 3\times 2\times \frac{\sqrt{15}}{4}+\frac{1}{2}\times 2\times 4\times \frac{\sqrt{15}}{4}\\
&=&\frac{3\sqrt{15}+4\sqrt{15}}{4}\\
&=&\frac{\color{black}{\fbox{\(\,\color{red}{ 7 }\,\)}}\sqrt{\color{black}{\fbox{\(\,\color{red}{ 15 }\)}\,}}}{\color{black}{\fbox{\(\,\color{red}{ 4 }\,\)}}}
\end{eqnarray}\)
垂直二等分線は\(\,2\,\)点\(\,\mathrm{A,C}\,\)から等しい距離にある点の集まりなので、
\(\,\mathrm{AD=AC}\,\)
が言えるので改めて余弦定理から、などとすることもできますが、誘導の通りに求めました。
これで〔1〕が終わりです。
第2問〔2〕データの活用(ヒストグラムと箱ひげ図と散布図の読み取り
〔2〕はデータの活用ですが、チンタラやってる時間はありません。
ちゃちゃっと済ませましょう。
(1)まずは箱ひげ図から度数分布表を選ぶ問題です。
\(\,2013\,\)年の箱ひげ図を見ると
最大値が\(\,136\,\)
最小値が\(\,72\,\)
くらいだということは読み取れます。
ところが、度数分布表を見ると最小値である\(\,72\,\)を含む階級
\(\,70\,\)以上\(\,80\,\)未満の階級
に度数を持っているのは③しかありません。
これだけで\(\color{black}{\fbox{\(\color{red}{ ③ }\)}}\)を選びます。
\(\,2017\,\)年の箱ひげ図を見ると
最大値が\(\,122\,\)
最小値が\(\,80\,\)
くらいだということは読み取れます。
最大値が\(\,120\,\)以上になるのは\(\,2012\,\)年、\(\,2013\,\)年、\(\,2017\,\)年のどれかです。
ヒストグラムの中で120以上の階級に度数を持つ①③④のうち、
①③は\(\,130\,\)以上にも度数がある。
だから2017年の同数分布表は\(\color{black}{\fbox{\(\, \color{red}{④} \,\)}}\)。
で何のデータだったっけ?
ソメイヨシノの開花日だったのか。
(2)モンシロチョウとツバメをはじめて見た日を追跡している人がいるんだな、と。
散布図には\(\,2\,\)点だけ重なったデータがあるということは散布図には\(\,39\,\)点あるはず。
モンシロチョウをはじめて見た日とツバメを初めて見た日の
箱ひげ図と散布図
を見ながら「正しくないもの」を選ぶのですべてを調べる方が良いですね。
・箱ひげ図から最初値は2つとも同じです。
・箱ひげ図から最大値が大きいのはモンシロチョウです。
・モンシロチョウの中央値(長方形の中の少し太い線)は\(\,93\,\)くらい
ツバメの中央値は\(\,91\,\)くらい
だからモンシロチョウの方が中央値は大きい。
・モンシロチョウの四分位範囲(箱ひげ図の長方形部分の幅)は\(\,20\,\)くらい
ツバメの四分位範囲は\(\,9\,\)くらい
だからモンシロチョウの四分位範囲はツバメの四分位範囲の\(\,3\,\)倍はない。
・だからモンシロチョウの四分位範囲は\(\,20\,\)くらいだって。
\(\,15\,\)日以下ではない。
これ間違い。
・だ・か・ら・、、、ツバメの四分位範囲は\(\,9\,\)くらいだから\(\,15\,\)日以下です。
・初見日が同じ地点は原点を通り傾きが\(\,1\,\)の直線上の点のことです。
見た目で\(\,4\,\)点ある、ということは重なりを考えなくても少なくとも\(\,4\,\)点あります。
・散布図にある切片の違いは、同じ地点での初見日の違いが\(\,15\,\)にはやいか遅いかの判断材料です。
例えば切片\(\,0\,\)上の点はモンシロチョウの初見日とツバメの初見日が同じ日だということを意味します。
そこで切片\(\,+15\,\)と\(\,-15\,\)の外にある点を見てみると
左の上にある点はモンシロチョウ\(\,69\,\)、ツバメ\(\,86\,\)
この差
\(\,86-69=17\,\)
が初見日の差です。
これだけで間違いだと分かりますが、もう\(\,1\,\)点、
モンシロチョウ\(\,104\,\)とツバメ\(\,88\,\)という点も
\(\,104-88=16\,\)
となるので15日以下だとは言えません。
これ正しくない。
よって\(\color{black}{\fbox{\(\, \color{red}{4} \,\)}}\)と\(\color{black}{\fbox{\(\, \color{red}{7} \,\)}}\)を選びます。
正しいものが多いから気がつきますが、正しくないものを探すので気をつけましょう。
(2)はここまでです。
とっとと次に行きましょう。
(3)
(1)と(2)のように(3)も続きじゃないのか?と思ったら最後にモンシロチョウとツバメが出てきました。
「一般に」ということは具体的にデータを作っちゃおう!
\(\,n≧2\,\)と一応書いてあるのでデータを2つにしようかな。
おまけして3つにしておこうかなと思いもしたけどめんどうなので2つにしよう。
\(\,x_1=-2\,,\,x_2=2\,\)
というデータに対し、
\(\displaystyle \color{red}{\bar{x}}=\frac{-2+2}{2}=\color{red}{0}\,\)
分散は
\(\begin{eqnarray}
s^2&=&\frac{(-2-0)^2+(2-0)^2}{2}\\
&=&\frac{4+4}{2}\\
&=&4
\end{eqnarray}\)
標準偏差は
\(\,\color{blue}{s}=\sqrt{4}=\color{blue}{2}\,\)
このとき
\(\displaystyle \,x’_1=\frac{-2-0}{2}=-1\,\)
\(\displaystyle \,x’_2=\frac{2-0}{2}=1\,\)
さて、とりあえず問題を解いていきましょうか。
・\(\,X\,\)の偏差\(\,x_1-\bar{x},x_2-\bar{x},\cdots,x_n-\bar{x}\,\)の平均値は\(\color{black}{\fbox{ テ }}\)である。
これは説明しなくても
偏差の和は\(\,0\,\)になるので平均値そのものも\(\,0\,\)になる。
というのはすぐに分かりますが先ほど作ったデータでも見ておきましょう。
一般に言えるなら、具体的なデータでも成り立っているはずです。
\(\,x_1=-2\,,\,x_2=2\,\)
\(\displaystyle \bar{x}=\frac{-2+2}{2}=0\,\)
\(\,s=2\,\)
これに
\(\,\displaystyle x’_i=\frac{x_i-\bar{x}}{s}\,\)
を適応させると
\(\,\displaystyle x’_1=\frac{-2-0}{2}=-1\,\)
\(\,\displaystyle x’_2=\frac{2-0}{2}=1\,\)
となります。
このデータの偏差は
\(\,x_1-\bar{x}=-2-0=-2\,\)
\(\,x_2-\bar{x}=2-0=2\,\)
この2つのデータの偏差の平均値は
\(\displaystyle \frac{-2+2}{2}=\color{black}{\fbox{\(\, \color{red}{0} \,\)}}\)
・\(\,X’\,\)の平均値は
\(\begin{eqnarray}\displaystyle
\bar{x’}&=&\frac{x’_1+x’_2}{2}\\
&=&\frac{-1+1}{2}=\color{black}{\fbox{\(\, \color{red}{0} \,\)}}
\end{eqnarray}\)
・\(\,X’\,\)の標準偏差は
\(\begin{eqnarray}\displaystyle
s’^2&=&\frac{(-1-0)^2+(1-0)^2}{2}\\
&=&\frac{2}{2}=1
\end{eqnarray}\)
なので
\(\,s’=\color{black}{\fbox{\(\, \color{red}{1} \,\)}}\,\)
これは一般にも言えないとおかしいでしょう?
「一般に」と書いてあるんだからこのデータにも成り立つはずです。
もちろん普通に文字のまま処理しても出てきますよ。
そちらはご自由にどうぞ。
最後は変換したデータの散布図を選ぶ問題です。
「標準偏差を考慮すると」
とあるので標準偏差が\(\,\color{red}{s’=1}\,\)だということを頭に置いておきましょう。
\(\,図5\,\)の散布図は問題ページが違っていて比較しにくいですが、
\(\,図4\,\)を圧縮した形になっています。
平均値からの差、偏差を見ると正負は一致するはずなので⓪か②の散布図だと予想がつきます。
ちなみに①③の散布図は\(\,\,(M’\,,\,N’\,)=(\,0\,,\,0\,)\,\)を中心に\(\,180\,\)°回転させた正負を逆にしたものです。
⓪と②で何が違うかというと\(\,M’,T’\,\)の絶対値が\(\,1\,\)の範囲にあるかどうかです。
\(\,-1≦M’≦1 , -1≦T’≦1\,\)
つまり
\(\,|M’|≦1 , |T’|≦1\,\)
なのかそうでないのかです。
「標準偏差を考慮して」
とヒントがあるので標準偏差を考えて見ましょう。
\(\displaystyle s’=\sqrt{\frac{(M’_1-\bar{M’})^2+(M’_2-\bar{M’})^2+\cdots+(M’_{41}-\bar{M’})^2}{41}}\,\)
において
\(\,s’=1 , \bar{M’}=0\,\)
なので両辺が正であることから
\(\begin{eqnarray}\displaystyle
1&=&\sqrt{\frac{M’^2_1+M’^2_2+\cdots+M’^2_{41}}{\color{red}{41}}}\\
1&=&\frac{M’^2_1+M’^2_2+\cdots+M’^2_{41}}{\color{red}{41}}\\
\color{red}{41}&=&M’^2_1+M’^2_2+\cdots+M’^2_{41}\\
\color{red}{41}&=&|M’_1|+|M’_2|+\cdots+|M’_{41}|
\end{eqnarray}\)
このとき右辺のすべてが\(\,1\,\)のとき成り立ちますがあり得ません。
\(\,0\,\)や\(\,0\,\)付近にもいくつも点があるので、
\(\,M’>1\,\)となる点は存在しないと標準偏差\(\,1\,\)というのは成り立ちません。
\(\,T’\,\)についても同じです。
だから\(\,M’\,,\,T’\,\)の散布図は\(\color{black}{\fbox{\(\, \color{red}{②} \,\)}}\)。
例えば\(\,図5\,\)の左下に並んである\(\,2\,\)点
\(\,(M’\,,\,T’)=(-1.9\,,\,-2.4)\,,\,(-1.6\,,\,-2.4)\,\)
これは明らかに\(\,図4\,\)の左下の\(\,2\,\)点でしょう。
\(\,図4\,\)で見ると
\(\,(M,T)=(69,69)\,,\,(73,69)\,\)
と見て、おおよその平均が中央値から大きくずれないと見て\(\,90\,\)前後だとすると、
変換値\(\,M’,T’\,\)は正の値にはならない、と思いません?
\(\,\displaystyle x’_i=\frac{x_i-\bar{x}}{s}\,\)
変換前の\(\,M,T\,\)の標準偏差\(\,s\,\)は正の値です。
この問題\(\,2\,\)点です。笑
勘で答えて\(\displaystyle \,\frac{1}{2}\,\)の確率です。
(なんていい加減な解説なんだ。w)
満点狙いでないなら、他の問題をきっちり仕上げて、それからで良いのではないでしょうか。
第1問は絶対体の外し方が問題になっただけでした。
⇒ 2019年(平成31年)度センター試験数学1Aの問1の解説
問3からは選択問題です。
例年通り、場合の数と確率、整数、平面幾何から\(\,2\,\)問選択です。
第\(\,2\,\)問までで\(\,60\,\)点あるので、平均は\(\,70\,\)点あってもおかしくはありません。
第\(\,3\,\)問は確率ですが条件付き確率を公式なしで解いておきました。
共通テストになっても内容が変わるわけではありません。