2019年度センター試験数学1Ａ第3問確率問題の解説

2019年(平成31年）度に行われたセンター試験の数学１Ａ第3問の確率問題の解説です。
第3問は条件付き確率までで終わりですが、色が紛らわしいだけで区別がしっかりできればそれほどややこしくはありません。
条件付き確率は公式を使わずに解説しておきます。

正解はセンターが発表していますので確認してください。

⇒　2019(H31)年センター試験数学1A問題

この問題は数学\(Ⅰ\mathrm{A}\)のみの部分掲載となります。

確率はルールの読み取りがポイント

(1)に入る前にこの問題のルール（条件）を確認しておきましょう。

　赤い袋には赤玉\(\,2\,\)個と白玉\(\,1\,\)個
　白い袋には赤玉\(\,1\,\)個と白玉\(\,1\,\)個

が入っています。

「赤い袋」に「赤い球」などと紛らわしいので
　
　赤い袋から取り出すことを\(\,\mathrm{A}\,\)、
　白い袋から取り出すことを\(\,\mathrm{B}\,\)

としておきましょう。
なので\(\,\mathrm{A}\,\)、\(\,\mathrm{B}\,\)という表現はこの解説内だけでの分け方なので意識しておいて下さい。

　\(\,\mathrm{\color{red}{A}}\,\)には赤球\(\,2\,\)個と白球\(\,1\,\)個
　\(\,\mathrm{\color{blue}{B}}\,\)には赤球\(\,1\,\)個と白球\(\,1\,\)個

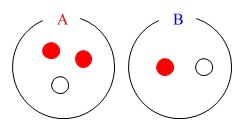
ということですが、問題の内容が変わるわけではありません。

ルールの続きです。

　最初にさいころを\(\,1\,\)個投げる。
　出目が\(\,3\,\)の倍数なら\(\,\mathrm{\color{blue}{B}}\,\)を選び、それ以外は\(\,\mathrm{\color{red}{A}}\,\)を選ぶ。
　選ばれた\(\,\mathrm{A,B}\,\)どちらかから球を\(\,1\,\)個取り出す。
　球の色を確認したら元に戻す。
　\(\,2\,\)回目と\(\,3\,\)回目は取り出した球の色と同じ色の袋から球を\(\,1\,\)個取り出し元に戻す。

ここで赤球、白球と書くと見にくいので、
（めんどうなのではありません。見にくいからです。）

　赤い袋\(\,\mathrm{A}\,\)から赤球を取り出すことを\(\,\mathrm{A}赤\,\)
　赤い袋\(\,\mathrm{A}\,\)から白球を取り出すことを\(\,\mathrm{A}白\,\)
　白い袋\(\,\mathrm{B}\,\)から赤球を取り出すことを\(\,\mathrm{B}赤\,\)
　白い袋\(\,\mathrm{B}\,\)から白球を取り出すことを\(\,\mathrm{B}白\,\)

と表現することにします。
この表現は自分で好きにして下さい。

例えば、
　赤い袋を\(\,\mathrm{R}\,\)、白い袋を\(\,\mathrm{W}\,\)として
　赤い球を\(\,r\,\)、白い球を\(\,w\,\)として
　赤い袋から白い球を取り出すときを\(\,\mathrm{A}w\,\)などとしても自分が分かり易ければ良いのです。

必要無いと思いますが袋選びの確率は出しておきましょうか。
　
　最初に\(\,\mathrm{A}\,\)を選ぶ確率\(\,\mathrm{P(A)}\,\)はさいころので目が\(\,3\,\)の倍数じゃないときなので
　\(\,\mathrm{P(A)}=\frac{4}{6}=\frac{2}{3}\,\)

　最初に\(\,\mathrm{B}\,\)を選ぶ確率\(\,\mathrm{P(B)}\,\)はさいころので目が\(\,3\,\)の倍数のときなので
　\(\,\mathrm{P(B)}=\frac{2}{6}=\frac{1}{3}\,\)

(1)
　\(\,\mathrm{A}\,\)が選ばれ赤球が取り出される「\(\,\mathrm{A}\,\)赤」の確率です。

最初に\(\,\mathrm{A}\,\)が選ばれる確率はさいころので目が\(\,3\,\)の倍数じゃないときなので、
\(\,\mathrm{A}\,\)から赤球を取り出すことを考えると
　\(\begin{eqnarray}\displaystyle
\mathrm{A}赤&=&\frac{4}{6}\times \frac{2}{3}\\
&=&\frac{\color{black}{\fbox{\(\,\color{red}{　4　}\,\)}}}{\color{black}{\fbox{\(\,\color{red}{　9　}\,\)}}}
\end{eqnarray}\)

次は\(\,\mathrm{B}赤\,\)です。
ここまでくるとルールにも慣れてきたでしょう。
サイコロので目が\(\,3\,\)の倍数なので
　\(\begin{eqnarray}\displaystyle
\mathrm{B}赤&=&\frac{2}{6}\times \frac{1}{2}\\
&=&\frac{\color{black}{\fbox{\(\,\color{red}{　1　}\,\)}}}{\color{black}{\fbox{\(\,\color{red}{　6　}\,\)}}}
\end{eqnarray}\)

(2)\(\,2\,\)回目の操作が\(\,\mathrm{B}\,\)で行われるのは、
　\(\,1\,\)回目に取り出された球が白の場合
で
　\(\,1\,\)回目が\(\,\mathrm{A白}\,\)、または\(\,\mathrm{B白}\,\)の場合
があるので
　\(\,\mathrm{A}白\,\)の確率\(\,\mathrm{P(A白)}\,\)と\(\,\mathrm{B}\,\)白の確率\(\,\mathrm{P(B白)}\,\)の和
です。
　\(\hspace{10pt}\mathrm{P(A白)+P(B白)}\\
\displaystyle =\frac{2}{3}\times \frac{1}{3}+\frac{1}{3}\times \frac{1}{2}\\
\displaystyle =\frac{2}{9}+\frac{1}{6}\\
\displaystyle =\frac{2\times 2+1\times 3}{18}\\
\displaystyle =\frac{\color{black}{\fbox{\(\color{red}{　7　}\)}}}{\color{black}{\fbox{\(\color{red}{　18　}\)}}}\)

(3)
「\(\,1\,\)回目の操作で白球を取り出す確率を\(\,p\,\)とすると」、
\(\,1\,\)回目の操作で赤球を取り出す確率は\(\,(1-p)\,\)です。

\(\,2\,\)回目の操作で白球が取り出される確率は、
・\(\,1\,\)回目が白球なら\(\,\mathrm{B}\,\)から白球を取り出す\(\,\mathrm{B白}\,\)
　\(\,1\,\)回目白　→　\(\,2\,\)回目\(\,\mathrm{B白}\,\)
・\(\,1\,\)回目が赤球なら\(\,\mathrm{A}\,\)から白球を取り出す\(\,\mathrm{A白}\,\)
　\(\,1\,\)回目赤　→　\(\,2\,\)回目\(\,\mathrm{A白}\,\)
の「和」なので、\(\,2\,\)回目に白球を取り出す確率は
　\(\hspace{10pt}\displaystyle p \times \frac{1}{2}+(1-p)\times \frac{1}{3}\\
\displaystyle =\frac{1}{2}p+\frac{1}{3}-\frac{1}{3}p\\
\displaystyle =\frac{\color{black}{\fbox{\(\color{red}{　1　}\)}}}{\color{black}{\fbox{\(\color{red}{　6　}\)}}}p+\frac{1}{3}\)

続きがあります。

\(\,p\,\)は\(\,1\,\)回目に白球を取り出す確率なので
(2)の\(\,2\,\)回目を\(\,\mathrm{B}\,\)で行う確率に等しいから
　\(\displaystyle \,p=\frac{7}{18}\,\)
これを代入すれば良いだけです。
　\(\hspace{10pt}\displaystyle \frac{1}{6}p+\frac{1}{3}\\
\displaystyle =\frac{1}{6}\times \frac{7}{18}+\frac{1}{3}\\
\displaystyle =\frac{7}{6\times 18}+\frac{1}{3}\\
\displaystyle =\frac{7+36}{6\times 18}\\
\displaystyle =\frac{\color{black}{\fbox{\(\color{red}{　43　}\)}}}{\color{black}{\fbox{\(\color{red}{　108　}\)}}}\)
　
「同様に」考えると」？

　\(\,2\,\)回目赤で\(\,3\,\)回目白
つまり
　\(\,2\,\)回目赤　→　\(\,\mathrm{A白}\,\)
と
　\(\,2\,\)回目白で\(\,3\,\)回目白
つまり
　\(\,2\,\)回目白　→　\(\,\mathrm{B白}\,\)
の確率の和を計算しろということですね。

\(\,2\,\)回目白の確率は\(\displaystyle \color{blue}{\frac{43}{108}}\)
なので\(\,2\,\)回目赤の確率は
　\(\displaystyle 1-\frac{43}{108}=\color{red}{\frac{65}{108}}\)

よって\(\,3\,\)回目に白球が取り出される確率は
　\(\,2\,\)回目赤　→　\(\,\mathrm{A白}\,\)
　\(\,2\,\)回目白　→　\(\,\mathrm{B白}\,\)
の和になるので
　\(\hspace{10pt}\displaystyle \color{red}{\frac{65}{108}}\times \frac{1}{3}+\color{blue}{\frac{43}{108}}\times \frac{1}{2}\\
\displaystyle =\frac{65\times 2+43\times 3}{108\times 3\times 2}\\
\displaystyle =\frac{130+129}{108\times 3\times 2}\\
\displaystyle =\frac{\color{black}{\fbox{\(\,\color{red}{　259　}\,\)}}}{\color{black}{\fbox{\(\,\color{red}{　648　}\,\)}}}\)

条件付き確率に公式を使わない方法

(4)は条件付き確率を求めます。

　\(\displaystyle \mathrm{P}_A(B)=\frac{\mathrm{P}(A\cap B)}{\mathrm{P}(A)}\)

という公式は覚えていると思うのでこれは使わずに答えを出しておきます。
何をするかというと『ベン図』を利用します。
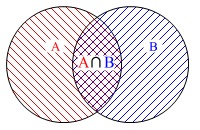ベン図の中には要素を書き込むのが普通ですが、ベン図の中にある要素の数と確率を考えます。
ここでは、
　\(\,\mathrm{A}\,\)と書いてある部分は\(\,\mathrm{A}\,\)が起こる確率
　\(\,\mathrm{B}\,\)と書いてある部分は\(\,\mathrm{B}\,\)が起こる確率
　\(\,\mathrm{A∩B}\,\)と書いているところは\(\,\mathrm{A∩B}\,\)が起こる確率
を表していると考えます。
　\(\,\mathrm{A}\,\)であったとき\(\,\mathrm{A∩B}\,\)の条件付き確率は　\(\displaystyle \frac{\mathrm{A\cap B}}{\mathrm{A}}\)
　\(\,\mathrm{B}\,\)であったとき\(\,\mathrm{A∩B}\,\)の条件付き確率は　\(\displaystyle \frac{\mathrm{A\cap B}}{\mathrm{B}}\)　
　
要素の数と全体の要素の数の比は確率を表すので、確率で考えてもベン図の状態は同じだと見るのです。

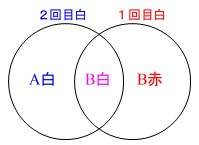
　「\(\,2\,\)回目の操作で取り出した球が白球」
の確率は(3)で
　\(\color{blue}{\mathrm{P}(\mathrm{A}白)}+\color{magenta}{\mathrm{P}(\mathrm{B}白)}=\displaystyle \frac{43}{108}\)

　「\(\,1\,\)回目の操作で取り出した球が白球」
の確率は(1)で
　\(\displaystyle \,p=\frac{7}{18}\,\)
とでているので、\(\,1\,\)回目白球で\(\,2\,\)回目も白球である確率は、
　\(\,1\,\)回目白　→　\(\,\mathrm{B}\,\)白
の確率で
　\(\displaystyle \color{magenta}{\mathrm{P}(\mathrm{B}白)}=\frac{7}{18}\times \frac{1}{2}=\color{magenta}{\frac{7}{36}}\)
求める条件付き確率は
　\(\begin{eqnarray}
\displaystyle \frac{\frac{7}{36}}{\frac{43}{108}}&=&\frac{7}{36} \div \frac{43}{108}\\
&=&\frac{7}{36}\times \frac{108}{43}\\
&=&\frac{\color{black}{\fbox{\(\color{red}{　21　}\)}}}{\color{black}{\fbox{\(\color{red}{　43　}\)}}}
\end{eqnarray}\)

やっていることは
　　\(\displaystyle \mathrm{P}_A(B)=\frac{\mathrm{P}(A\cap B)}{\mathrm{P}(A)}\)
と同じじゃないか！
公式を覚えている人はそう思えるでしょう。

公式を忘れたときでも、覚えていなくても、ベン図で出せますよ、というだけです。

だから最初に断り書きしてるでしょう？
きれいな解答を求めている人は予備校の解答を見て下さい。

このサイトでは、泥臭い解答を目指しています。笑
（何を目指しているんだ？）

もう一つ条件付き確率がありました。

　「3回目の操作で取り出した球が白球だったとき」
の確率は(3)で
　\(\displaystyle \color{red}{\frac{259}{648}}\)
と求めてあります。

　「はじめて白球が取り出されたのが\(\,3\,\)回目である」
確率は、
　\(\,1\,\)回目赤　→　\(\,2\,\)回目赤　→　\(\,3\,\)回目白
の場合なので

\(\,1\,\)回目赤である場合は
　\(\,\mathrm{A赤}\,\)と\(\,\mathrm{B赤}\,\)
があるので確率は
　\(\hspace{10pt}\displaystyle \frac{2}{3}\times \frac{2}{3}+\frac{1}{3}\times \frac{1}{2}\\
\displaystyle =\frac{4}{9}+\frac{1}{6}\\
\displaystyle =\frac{4\times 2+1\times 3}{18}\\
\displaystyle =\frac{11}{18}\)

※
これは(2)の\(\,2\,\)回目が\(\,\mathrm{B}\,\)で行われるという事象の余事象なので
　\(\displaystyle 1-\frac{7}{18}=\frac{11}{18}\)
と同じことです。

\(\,2\,\)回目も赤である場合は\(\,1\,\)回目赤でさらに\(\,2\,\)回目も赤
　\(\,1\,\)回目赤　→　\(\,\mathrm{A赤}\,\)
の場合の確率なので
　\(\displaystyle \frac{11}{18}\times \frac{2}{3}=\frac{11}{27}\)

この後3回目が\(\,\mathrm{A白}\,\)となる確率は\(\displaystyle \frac{1}{3}\)なので
　\(\displaystyle \frac{11}{27}\times \frac{1}{3}=\color{blue}{\frac{11}{81}}\)
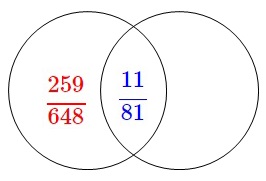（なんて手を抜いた図なんだ！）
よって求める条件付き確率は
　\(\hspace{10pt}\displaystyle \frac{\color{blue}{\frac{11}{81}}}{\color{red}{\frac{259}{648}}}\\
\displaystyle =\color{blue}{\frac{11}{81}}\div \color{red}{\frac{259}{648}}\\
\displaystyle =\frac{11}{81}\times \frac{648}{259}\\
\displaystyle =\frac{\color{black}{\fbox{\(\,\color{red}{　88　}\,\)}}}{\color{black}{\fbox{\(\,\color{red}{　259　}\,\)}}}\)
　
第3問の確率終わりです。
急いで入力したので入力ミスしてそうです。笑