2019年(平成31年度)に行われた平成最後のセンター試験となる数学1Aの問1の解説です。
問1は絶対値のはずし方、命題の必要十分性、2次関数の平行移動問題で項目としては例年通りです。
数式だけでも処理できるようになっていますがグラフを活用すると分かり易い問題もあります。
正答はセンターが発表していますので確認してください。
この問題は数学\(ⅠＡ\)の部分のみの問題です。
※
きれいな解答を見たい人は予備校の解答などを参考にして下さい。
ここではとにかく答えを出す、という方針で進めます。笑
2019年センター試験数学ⅠＡ第１問〔１〕数と式と絶対値
数式を完全平方式にします。
\(9a^2-6a+1=(\,\color{black}{\fbox{ ア }}a-\color{black}{\fbox{ イ }}\,)^2\)
平方して
\(\,9\,\)になる数は\(\,3\,\)
\(\,1\,\)になる数は\(\,1\,\)
なので問題はないでしょう。
\(9a^2-6a+1=(\color{black}{\fbox{\(\,\color{red}{ 3 }\,\)}}a-\color{black}{\fbox{\(\,\color{red}{ 1 }\,\)}})^2\)
使っているのは
\((a+b)^2=a^2+2ab+b^2\)
の逆で因数分解公式
\(a^2+2ab+b^2=(a+b)^2\)
で\(\,+b\,\)の代わりに\(\,-b\,\)を入れた
\(\color{red}{a^2-2ab+b^2=(a-b)^2}\)
において\(\,a\,\)に\(\,3a\,\)、\(\,b\,\)に\(\,1\,\)を代入たものです。
中学生でもできる問題です。
この\(\,\color{blue}{9a^2+6a+1}\,\)は次に出てくる
\(\,\mathrm{A=\sqrt{\color{blue}{9a^2-6a+1}}+|a+2|}\,\)
のルートの中身です。
それが誘導されています。
\(\begin{eqnarray}
A=\sqrt{(3a-1)^2}+|a+2|
\end{eqnarray}\)
これはルートをはずすときに注意が必要ですが問題ないでしょう。
問題が多いのでここでは説明を省略します。
\(\sqrt{(3a-1)^2}=|3a-1|\)
です。
すると
\(\,A=|3a-1|+|a+2|\,\)
この場合分けは絶対値の中身が\(\,0\,\)になるところを境界に分かれます。
\(\,3a-1=0\,\) から \(\displaystyle a=\frac{1}{3}\)
\(\,a+2=0\,\) から \(a=-2\)
この2点を境界に3つに分かれます。
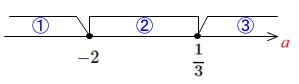問題では③②①の順に場合分けされています。
③ \(\displaystyle a＞\frac{1}{3}\)のとき、
例えば\(\,a=1\,\)などを入れて
\(\,3a-1＞0 , a+2＞0\,\)
（絶対値の中は両方正）なので
\(\begin{eqnarray}
A&=&|3a-1|+|a+2|\\
&=&(3a-1)+(a+2)\\
&=&\color{black}{\fbox{\(\,\color{red}{ 4 }\,\)}}a+\color{black}{\fbox{\(\,\color{red}{ 1 }\,\)}}
\end{eqnarray}\)
② \(\displaystyle -2≦a≦\frac{1}{3}\)のとき、
例えば\(\,a=0\,\)などを入れて
\(\,3a-1≦0 , a+2≧0\,\)
なので
\(\begin{eqnarray}
A&=&|3a-1|+|a+2|\\
&=&-(3a-1)+(a+2)\\
&=&-3a+1+a+2\\
&=&\color{black}{\fbox{\(\,\color{red}{ -2 }\,\)}}a+\color{black}{\fbox{\(\,\color{red}{ 3 }\,\)}}
\end{eqnarray}\)
① \(\,a＜-2\,\)のとき
例えば\(\,a=-3\,\)などを入れて
\(\,3a-1＜0 , a+2＜0\,\)
なので
\(\begin{eqnarray}
A&=&|3a-1|+|a+2|\\
&=&-(3a-1)-(a+2)\\
&=&-3a+1-a-2\\
&=&-\color{black}{\fbox{ 4 }}a-\color{black}{\fbox{ 1 }}
\end{eqnarray}\)
次に
\(\,A=\color{magenta}{2a+13}\,\)
を満たす\(\,a\,\)を求めます。
①②③の場合分けをしたように\(\,a\,\)の範囲で\(\,A\,\)が変わります。
\(\displaystyle a＞\frac{1}{3}\) のとき \(\,A=\color{blue}{4a+1}\,\)
なので
\(\begin{eqnarray}
\color{blue}{4a+1}&=&\color{magenta}{2a+13}\\
2a&=&12\\
a&=&\color{black}{\fbox{\(\,\color{red}{ 6 }\,\)}}
\end{eqnarray}\)
これは \(\displaystyle a＞\frac{1}{3}\) に適しています。
\(\displaystyle -2≦a≦\frac{1}{3}\) のとき \(\,A=\color{blue}{-2a+3}\,\)
なので
\(\begin{eqnarray}\displaystyle
\color{blue}{-2a+3}&=&\color{magenta}{2a+13}\\
-4a&=&10\\
&=&-\frac{5}{2}
\end{eqnarray}\)
これは \(\displaystyle -2≦a≦\frac{1}{3}\) に不適。
\(\,a＜-2\,\) のとき \(\,A=\color{blue}{-4a-1}\,\)
なので
\(\begin{eqnarray}\displaystyle
\color{blue}{-4a-1}&=&\color{magenta}{2a+13}\\
-6a&=&14\\
a&=&\frac{\color{black}{\fbox{\(\,\color{red}{ -7 }\,\)}}}{\color{black}{\fbox{\(\,\color{red}{ 3 }\)}}\,}
\end{eqnarray}\)
これは \(\,a＜-2\,\) に適しています。
第一問の〔１〕は終わりです。
次に第一問の〔２〕です。
第１問〔２〕命題（必要条件と十分条件）
条件を見ておきましょう。
\(\,p\,\) : \(\,m\,\)と\(\,n\,\)はともに奇数である。
\(\,q\,\) : \(\,3mn\,\)は奇数である。
\(\,r\,\) : \(\,m+5n\,\)は偶数である。
\(\,p\,\)の「\(\,m\,\)と\(\,n\,\)はともに」
は
「\(\,m\,\)かつ\(\,n\,\)」
の意味で、「かつ」の否定は「または」になるので、
\(\,\bar{p}\,\) : \(\,m\,\)または\(\,n\,\)は偶数である。
(1)自然数\(\,m,n\,\)が条件\(\,\bar{p}\,\)を満たす。
\(\,\bar{p}\,\) : \(\,m\,\)または\(\,n\,\)は偶数である。
どちらかは偶数で、\(\,m\,\)が奇数なら\(\,n\,\)は\(\color{black}{\fbox{\(\,\color{red}{ 偶数 }\,\)}}\)でなければなりません。
また、「\(\,m\,\)または\(\,n\,\)が偶数」の「または」は排他的ではありません。
⇒ 数学１Ａ 命題と逆に使う「かつ」と「または」と日常生活の違い
両方が偶数でも良いということなので、
\(\,m\,\)が偶数ならば\(\,n\,\)は\(\color{black}{\fbox{\(\, \color{red}{偶数でも奇数でもよい} \,\)}}\)。
となります。
(2)は反例を探せ！です。
・「\(\,p\,\)は\(\,q\,\)であるための\(\color{black}{\fbox{ セ }}\)」
\(\,p \rightleftharpoons q\,\) の両方を見ます。
\(\,p \rightarrow q\,\)
は
「\(\,m\,\)と\(\,n\,\)がともに奇数ならば\(\,3mn\,\)は奇数である。」
なので常に成り立つ。
\(\,\rightarrow\,\) は○（十分）
\(\,p \leftarrow q\,\)
は
「\(\,3mn\,\)が奇数であるならば\(\,m\,\)と\(\,n\,\)はともに奇数。」
なので常に成り立つ。
\(\,\leftarrow\,\) は○（必要）
よって\(\color{black}{\fbox{\(\,\color{red}{ 必要十分条件 }\,\)}}\)。
・「\(\,p\,\)は\(\,r\,\)であるための\(\color{black}{\fbox{ ソ }}\)」
\(\,p \rightarrow r\,\)
は
「\(\,m\,\)と\(\,n\,\)がともに奇数ならば\(\,m+5n\,\)は偶数である。」
\(\,m,n\,\)が奇数のとき、\(\,m\,\)は奇数、\(\,5n\,\)も奇数です。
\(\,(奇数)+(奇数)=(偶数)\,\)
なので
\(\,\rightarrow\,\) は○（十分）
\(\,p \leftarrow r\,\)
は
「\(\,m+5n\,\)は偶数ならば\(\,m\,\)と\(\,n\,\)がともに奇数である。」
\(\,m,n\,\)ともに偶数のとき、
\(\,m\,\)は偶数、\(\,5n\,\)も偶数で、\(\,m+5n\,\)は偶数
になるので、\(\,m,n\,\)ともに奇数とは言えない。
\(\,p \leftarrow r\,\) は×
よって\(\color{black}{\fbox{\(\,\color{red}{ 十分条件ではあるが必要条件ではない }\,\)}}\)。
・「「\(\,\bar{p}\,\)は\(\,r\,\)であるための\(\color{black}{\fbox{ タ }}\)」
\(\,\bar{p} \rightarrow r\,\)
は
「\(\,m\,\)または\(\,n\,\)が偶数ならば\(\,m+5n\,\)は偶数である。」
\(\,m\,\)が奇数、\(\,n\,\)が偶数のとき、
\(\,m+5n\,\)は奇数になるので\(\,m+5n\,\)は偶数であるとは言えない。
\(\,\bar{p} \rightarrow r\,\) は×
\(\,\bar{p} \leftarrow r\,\)
は
「\(\,m+5n\,\)は偶数ならば\(\,m\,\)または\(\,n\,\)が偶数である。」
\(\,m,n\,\)ともに奇数のとき、
\(\,m+5n\,\)は偶数になるので\(\,m\,\)または\(\,n\,\)が偶数であるとは言えない。
\(\,\bar{p} \leftarrow r\,\) は×
よって\(\color{black}{\fbox{\(\,\color{red}{ 十分条件でも必要条件でもない }\,\)}}\)。
具体的な数字を入れていっても良いですが、それほどややこしい条件ではないですね。
第１問〔３〕2次関数の平行移動
２次関数を見たら平方完成するでしょう。
\(y=x^2+(2a-b)x+a^2+1\)
あれ？計算力試している？
\(\begin{eqnarray}\displaystyle
y&=&x^2+(2a-b)x+a^2+1\\
&=&\left(x+\frac{2a-b}{2}\right)^2-\frac{(2a-b)^2}{4}+a^2+1\\
&=&\left(x+\frac{2a-b}{2}\right)^2+\frac{-(2a-b)^2+4(a^2+1)}{4}\\
&=&\left(x+\frac{2a-b}{2}\right)^2+\frac{-(4a^2-4ab+b^2)+4a^2+4}{4}\\
&=&\left(x+\frac{2a-b}{2}\right)^2+\frac{-4a^2+4ab-b^2+4a^2+4}{4}\\
&=&\left(x+\frac{2a-b}{2}\right)^2+\frac{4ab-b^2+4}{4}\\
&=&\left(x+\frac{2a-b}{2}\right)^2+ab-\frac{b^2}{4}+1
\end{eqnarray}\)
(1)頂点は
\(\displaystyle \left(\frac{b}{\color{black}{\fbox{\(\color{red}{ 2 }\)}}}-a\,,\,-\frac{b^2}{\color{black}{\fbox{\(\color{red}{ 4 }\)}}}+ab+1\,\right)\)
(2)2次関数が\(\,(-1,6)\,\)を通る。
頂点が\(\,(-1,6)\,\)なのではありません。
平方完成した形より、もとの関数に代入した方がはやいでしょう。
\(\begin{eqnarray}
y&=&x^2+(2a-b)x+a^2+1\\
(6(&=&(-1)^2+(2a-b)\times (-1)+a^2+1\\
&=&+1-2a+b+a^2+1\\
b&=&-a^2+2a+4\\
&=&-(a^2-a)+4\\
&=&-(a-1)^2+1+4\\
&=&-(a-1)^2+5
\end{eqnarray}\)
\(\,(a,b)\,\)の関数は上に凸な放物線となるので
\(\,b\,\)の最大値は\(\,b=\color{black}{\fbox{\(\,\color{red}{ 5 }\,\)}}\,\)
そのときの\(\,a\,\)の値は\(\,a=\color{black}{\fbox{\(\,\color{red}{ 1 }\,\)}}\,\)
\(\,b=5\,,\,a=1\,\)のときもとの2次関数は
\(\begin{eqnarray}\displaystyle
y&=&x^2+(2a-b)x+a^2+1\\
&=&x^2+(2\times 1-5)x+(1)^2+1\\
&=&x^2-3x+2\\
&=&\left(x-\frac{3}{2}\right)^2-\frac{9}{4}+2\\
&=&\left(x-\frac{3}{2}\right)^2+\frac{-9+8}{4}\\
&=&\left(x-\frac{3}{2}\right)^2-\frac{1}{4}
\end{eqnarray}\)
この放物線の頂点は
\(\displaystyle \left(\frac{3}{2}\,,\,-\frac{1}{4}\right)\)
よって原点が頂点の放物線\(\,y=x^2\,\)を
\(\,x\,\)軸方向に \(\displaystyle \frac{\color{black}{\fbox{\(\color{red}{ 3 }\)}}}{\color{black}{\fbox{\(\color{red}{ 2 }\)}}}\)
\(\,y\,\)軸方向に \(\displaystyle \frac{\color{black}{\fbox{\(\color{red}{ -1 }\)}}}{\color{black}{\fbox{\(\color{red}{ 4 }\)}}}\)
だけ平行移動したものである。
放物線が合同なので頂点の移動分だけ平行移動していることになります。
(1)で平方完成した頂点
\(\displaystyle \left(\frac{b}{2}-a\,,\,-\frac{b^2}{4}+ab+1\,\right)\)
を利用すると\(\,b=\color{red}{5}\,,\,a=\color{blue}{1}\,\)を代入して
\(\,x\,\)座標は
\(\hspace{10pt}
\displaystyle \frac{b}{2}-a\\
\displaystyle =\frac{\color{red}{5}}{2}-\color{blue}{1}\\
\displaystyle =\frac{3}{2}
\)
\(\,y\,\)座標は
\(\hspace{10pt}\displaystyle -\frac{b^2}{4}+ab+1\\
\displaystyle =-\frac{\color{red}{5}^2}{4}+\color{blue}{1}\times \color{red}{5}+1\\
\displaystyle =-\frac{25}{4}+5+1\\
\displaystyle =-\frac{1}{4}
\)
どちらが計算量が少なく感じるか試験場では微妙ですね。
なんとなくもとの関数の方が楽かな？と進めましたが、どっちでもよかったようです。
これで第1問が終わりです。
自分でやればかなり短時間で終わったでしょう？
例年のことを考えるとデータの読み取りが待っているので時間は稼いでおきたいところです。
⇒ 2019年度センター試験数学1Aの問2三角比とデータの活用の解説
第2問は三角比、データの分析です。
問題のページ数の割に、、、でしたね。
「一般的に」、って具体的にも通じないとダメなんですよね。
第\(\,3\,\)問以降はまとめページから選んで見てください。