2020年(令和2年)度に行われた最後のセンター試験、数学1Ａの第1問の解説です。
直線の傾きと不等式（数と式）、集合と命題、2次関数という問題構成は例年通りです。
この基本的な大切な項目が出題されるのは共通テストになっても変わらないでしょう。
センター試験2020年度数学\(\,\mathrm{ⅠＡ}\,\)の問題です。
第１問
第\(\,1\,\)問は〔\(\,1\,\)〕\(\,1\,\)次関数と不等式、〔\(\,2\,\)〕集合と命題と反例、〔\(\,3\,\)〕\(\,2\,\)次関数です。
毎年のことですが配点が\(\,30\,\)点あるので確実に取っておきたい\(\,1\,\)問です。
〔 1 〕数と式（1次関数）と不等式
「数と式」とは書きましたが、\(1\,\)次関数を扱うことになるので数式だけで考えるのではなくグラフをイメージしながら考えましょう。
(1)
直線 \(\,\ell\,\)は
\(\,y=(\color{red}{a^2-2a-8})x+\color{blue}{a}\,\)
です。
直線ですよ、直線。中学生みたいです。
傾きが \(\,\color{red}{a^2-2a-8}\,\)
\(\,y\,\)切片が \(\,\color{blue}{a}\,\)
傾きが負となるのは、
\(\,\color{red}{a^2-2a-8}＜0\,\)
となるときなので、
\(\hspace{10pt}a^2-2a-8\\
=(a+2)(a-4)＜0\)
から
\(\color{black}{\fbox{ －2 }}\,＜\,a\,＜\,\color{black}{\fbox{ 4 }}\)
アイ \(\,\underline{ -2 }\,\) ウ \(\,\underline{ 4 }\,\)
(2)
\(\,\color{red}{a^2-2a-8}\,\)というのは「傾き」のことです。
\(\color{red}{a^2-2a-8}≠0\)
傾きが\(\,0\,\)ではない、つまり直線\(\,\ell\,\)が\(\,x\,\)軸に平行ではないときを考えます。
直線\(\,\ell\,\)と\(\,x\,\)軸との交点の\(\,x\,\)座標が\(\,\color{magenta}{b}\,\)なので、
\(\,x\,\)切片が\(\,\color{magenta}{b}\,\)です。
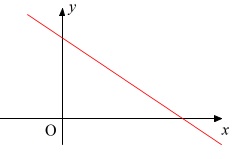
\(\,\color{blue}{a}＞0\,\)の場合、\(\,\color{magenta}{b}＞0\,\)となるのは
\(\,\color{blue}{a}\,\)は\(\,\ell\,\)の\(\,y\,\)切片なので、
\(\,y\,\)軸との交点が\(\,x\,\)軸よりも上にあるときです。
簡単に言えば、
\(\,\color{blue}{a}＞0\,\) かつ 右下がりになるとき
なので、
\(\,\color{blue}{a}＞0\,\) かつ \(\,\color{red}{a^2-2a-8}＜0\,\)
この不等式は(1)で解いているので、
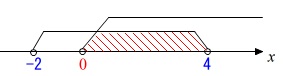\(\,\color{black}{\fbox{ 0 }}\,＜\,a\,＜\,\color{black}{\fbox{ 4 }}\,\)
エ \(\,\underline{ 0 }\,\) オ \(\,\underline{ 4 }\,\)
次に、\(\,\color{blue}{a}\,≦\,0\,\)の場合、\(\,\color{magenta}{b}\,＞\,0\,\)となるのは
\(\,y\,\)切片がマイナス
\(\,x\,\)切片がプラス
だから
傾き\(\,\color{red}{a^2-2a-8}\,\)がプラス
のときなので、
\(\,\color{blue}{a}≦0\,\)かつ\(\,\color{red}{a^2-2a-8}＞0\,\)
\(\hspace{10pt} a^2-2a-8\\
=(a+2)(a-4)＞0\)
から
\(\,a\,＜\,-2\,,\,4\,＜\,a\,\)
\(\,a≦0\,\)のときを見ているので
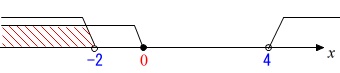\(a\,＜\,\color{black}{\fbox{ －2 }}\)
カキ \(\,\underline{ -2 }\,\)
続いて、\(\,a=\sqrt{3}\,\)のとき
直線\(\,\ell\,\)は
\(\begin{eqnarray}
y&=&\{(\sqrt{3})^2-2(\sqrt{3})-8\}x+\sqrt{3}\\
&=&(3-2\sqrt{3}-8)x+\sqrt{3}\\
&=&(-5-2\sqrt{3})x+\sqrt{3}
\end{eqnarray}\)
この直線の\(\,x\,\)切片は\(\,y=0\,\)とおいて
\(\begin{eqnarray}\displaystyle
0&=&(-5-2\sqrt{3})x+\sqrt{3}\\
(5+2\sqrt{3})x&=&\sqrt{3}\\
x&=&\frac{\sqrt{3}}{5+2\sqrt{3}}\\
&=&\frac{\sqrt{3}(5-2\sqrt{3}}{(5+2\sqrt{3})(5-2\sqrt{3})}\\
&=&\frac{5\sqrt{3}-6}{25-12}\\
&=&\frac{\color{black}{\fbox{ 5 }}\sqrt{\color{black}{\fbox{ 3 }}}-\color{black}{\fbox{ 6 }}}{\color{black}{\fbox{ 13 }}}
\end{eqnarray}\)
ク \(\,\underline{ 5 }\,\) ケ \(\,\underline{ 3 }\,\) コ \(\,\underline{ 6 }\,\) サシ \(\,\underline{ 13 }\,\)
こんなところで時間をかけている場合ではありません。
直線とか\(\,x\,\)座標とかグラフを示す言葉が問題にあるんだから数式だけで処理しようとしないことです。
〔 2 〕集合と命題（要素と反例）
集合で使う用語と記号が分かっていればここも簡単です。
条件\(\,p\,\)：\(\,n\,\)は\(\,4\,\)の倍数
条件\(\,q\,\)：\(\,n\,\)は\(\,6\,\)の倍数
条件\(\,r\,\)：\(\,n\,\)は\(\,24\,\)の倍数
具体的に書き出すと集合は
\(\,P=\{\,4,8,\color{blue}{12},16,20,\color{red}{24},28,32,\color{blue}{36},\cdots\,\}\,\)
\(\,Q=\{\,6,\hspace{8pt}\color{blue}{12},\hspace{6pt}18,\hspace{10pt}\color{red}{24},30,\hspace{14pt}\color{blue}{36},\cdots\,\}\,\)
\(\,R=\{\hspace{62pt}\,\color{red}{24},\hspace{36pt}\color{red}{48},\cdots\,\}\,\)
手書きだと\(\,30\,\)秒くらいで終わります。
(1)
\(\,32 \in \color{black}{\fbox{ス}}\,\)
「\(x\,\in\,\mathrm{A}\)」は「\(\,x\,\)は集合\(\,\mathrm{A}\,\)の要素」を意味します。
\(\,32\,\)を要素に持つ集合は\(\,P\,\)だけで、
\(\,P\,\)の要素だけを意味するのは②の\(\,P\cap \overline{Q}\,\)
ス \(\,\underline{ ② }\,\)
集合\(\,P\,\)の要素を含む集合は⓪と①もありますが、\(\,Q\,\)との交わりに\(\,32\,\)はありません。
(2)
集合\(\,P\,\)と集合\(\,Q\,\)の交わりの要素の中で最小のものは、
\(\,4\,\)と\(\,6\,\)の最小公倍数なので\(\,\color{black}{\fbox{ 12 }}\,\)です。
セソ \(\,\underline{ 12 }\,\)
また、この\(\,12\,\)は集合\(\,R\,\)の要素ではありません。
\(\,12\,\color{black}{\fbox{ \(\,\notin\,\) }} \,R\,\)
タ \(\,\underline{ ④ }\,\)
問題中の同じ記号には、同じ数字や記号が入るので問題をながめているのではなく書き込むのですよ。
(3)
自然数\(\,12\,\)はどの命題の反例になっているか、です。
「反例」は1つでもあればその命題が「偽」となります。
もう一度、要素を並べておきます。
\(\,P=\{\,4,8,\color{blue}{12},16,20,\color{red}{24},28,32,\color{blue}{36},\cdots\,\}\,\)
\(\,Q=\{\,6,\hspace{8pt}\color{blue}{12},\hspace{6pt}18,\hspace{10pt}\color{red}{24},30,\hspace{14pt}\color{blue}{36},\cdots\,\}\,\)
\(\,R=\{\hspace{62pt}\,\color{red}{24},\hspace{36pt}\color{red}{48},\cdots\,\}\,\)
⓪ \((\,p\,かつ\, q \,)\,\Rightarrow \,\overline{r}\,\)
\(\,p\,\)かつ\(\,q\,\)ならば\(\,r\,\)ではない。
「\(\,4\,\)の倍数かつ\(\,6\,\)の倍数」
（\(\,12\,\)の倍数）
\(\,12,24,36,48,\cdots\,\)
ならば
「\(\,24\,\)の倍数でない。」
この反例は\(\,\color{red}{24}\,\)の倍数です。
① \((\,p\,または\, q \,)\,\Rightarrow \,\overline{r}\,\)
\(\,p\,\)または\(\,q\,\)ならば\(\,r\,\)ではない。
「\(\,4\,\)の倍数または\(\,6\,\)の倍数」
\(\hspace{10pt}4,6,8,12,\\
16,18,20,24,\\
28,30,32,\cdots\,\)
ならば
「\(\,24\,\)の倍数でない。」
この反例も\(\,\color{red}{24}\,\)の倍数です。
② \(\,r\,\Rightarrow \,(p\,かつ\,q\,)\,\)
\(\,r\,\)ならば\(\,p\,\)かつ\(\,q\,\)である。
「\(\,24\,\)の倍数」
\(24,48,72,96,\cdots\)
ならば
「\(\,4\,\)の倍数かつ\(\,6\,\)の倍数である。」
（「\(\,12\,\)の倍数である。」）
この命題は「真」なので反例はありません。
③ \(\,(p\,かつ\,q\,)\Rightarrow \,\,r\,\)
\(\,p\,\)かつ\(\,q\,\)ならば\(\,r\,\)である。
「\(\,4\,\)の倍数かつ\(\,6\,\)の倍数」
\(12,24,36,48,\cdots\,\)
（\(\,12\,\)の倍数）
ならば
「\(\,24\,\)の倍数である。」
これです。
\(\,12\,\)が反例になっています。
チ \(\,\underline{ ③ }\,\)
集合\(\,P,Q,R\,\)の要素を書き出した数字の並びだけで最後まで終わりました。
〔 3 〕2次関数と連立不等式
原点を頂点とする\(\,2\,\)次関数\(\,y=x^2\,\)のグラフを書いて、
問題通りに平行移動させていけば大した計算もありません。
(1)
\(\,x\,\)軸上の\(\,2\,\)点\(\,(\,c\,,\,0\,),(\,c+4\,,\,0\,)\,\)を通るので、
この放物線の軸は
\(\displaystyle x=\frac{c+c+4}{2}=c+2\)
です。
一般に放物線は軸に対称なので、
\(\,y\,\)座標が同じ\(\,2\,\)点の中点を通る\(\,y\,\)軸に平行な直線を軸とします。
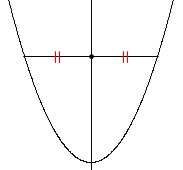ただし、これは\(\,y=0\,\)が\(\,c,c+4\,\)を2つの解とするので、
（\(\,x\,\)軸との交点が\(\,c,c+4\,\)なので）
\(\begin{eqnarray}
y&=&(x-c)\{x-(c+4)\}\\
&=&x^2-(c+4)x-cx+c(c+4)\\
&=&x^2-(c+4+c)x+c(c+4)\\
&=&x^2-2(c+\color{black}{\fbox{ 2 }})x+c(c+\color{black}{\fbox{ 4 }})
\end{eqnarray}\)
ツ \(\,\underline{ 2 }\,\) テ \(\,\underline{ 4 }\,\)
\(\,x\,\)軸との交点が\(\,\color{red}{\alpha}\,,\,\color{blue}{\beta}\,\)のとき
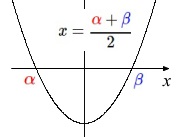放物線は
\(y=a(x-\color{red}{\alpha})(x-\color{blue}{\beta})\)
となります。
軸は\(\displaystyle \,x=\frac{\color{red}{\alpha}+\color{blue}{\beta}}{2}\)です。
軸が\(\,x=c+2\,\)だとすると放物線は
\(y=\{(x-(c+2)\}^2+b\)
とおけて、これは\(\,(\,c\,,\,0\,)\,\)を通ることから
\(\,b=-4\,\)
よって、
\(\begin{eqnarray}
y&=&\{x-(c+2)\}^2-4\\
&=&x^2-2(c+2)x+(c+2)^2-4\\
&=&x^2-2(c+2)x+c(c+4)
\end{eqnarray}\)
としても大した差はありませんね。
\(\,2\,\)次関数\(\,\mathrm{G}\,\)を
\(\begin{eqnarray}
y&=&\color{red}{f(x)}\\
&=&x^2-2(c+2)x+c(c+4)
\end{eqnarray}\)
としておきます。
\(\,2\,\)点\(\,(\,3\,,\,\color{red}{0}\,),(\,3\,,\color{blue}{-3}\,)\,\)を両端とする線分と共有点をもつとき、
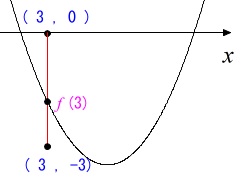\(\,\color{blue}{-3}≦f(3)≦\color{red}{0}\,\)
となっているはずです。
\(\begin{eqnarray}
f(3)&=&(3)^2-2(c+2)(3)+c(c+4)\\
&=&9-6c-12+c^2+4c\\
&=&c^2-2c-3
\end{eqnarray}\)
なので、
\(\,\color{blue}{-3}≦\color{magenta}{c^2-2c-3}≦\color{red}{0}\,\)
この連立不等式を解くと、
\(\color{blue}{-3}≦\color{magenta}{c^2-2c-3}\)
から
\(c\,≦\,0\,,\,2\,≦\,c\) ･･･①
また
\(\,\color{magenta}{c^2-2c-3}≦\color{red}{0}\,\)
から
\(\,-1\,≦\,c\,≦3\,\) ･･･②
①②より
\(\,-\color{black}{\fbox{ 1 }}\,≦\,c\,≦\,\color{black}{\fbox{ 0 }}\) , \(\,\color{black}{\fbox{ 2 }}\,≦\,c\,≦\,\color{black}{\fbox{ 3 }}\,\)
ト \(\,\underline{ 1 }\,\) ナ \(\,\underline{ 0 }\,\) ニ \(\,\underline{ 2 }\,\) ヌ \(\,\underline{ 3 }\,\)
(2)
問題により\(\,2\,≦\,c\,≦\,3\,\)の場合で考えますが、
軸が\(\,x=3\,\)より右側にある場合、ということくらい分かっていれば良いです。
\(\,G\,\)が点\(\,(\,\color{red}{3}\,,\,\color{blue}{-1}\,)\,\)を通るので、
\(\,f(\color{red}{3})=c^2-2c-3=\color{blue}{-1}\,\)
つまり
\(\,c^2-2c-2=0\,\)
これから（因数分解できないので解の公式です。）
\(\begin{eqnarray}\displaystyle
c&=&\frac{1 \pm \sqrt{1^2-1(-2)}}{1}\\
&=&1\pm \sqrt{3}
\end{eqnarray}\)
\(\,2\,≦\,c\,≦\,3\,\)の場合を見ているので、
\(c=1+\sqrt{3}\)
このとき\(\,G\,\)は
\(\begin{eqnarray}
y&=&x^2-2(c+2)x+c(c+4)\\
&=&\{x-(c+2)\}^2-4\\
&=&\{x-(1+\sqrt{3}+2)\}^2-4\\
&=&\{x-(3+\sqrt{3})\}^2-4
\end{eqnarray}\)
この放物線の頂点は
\(\,(\,3+\sqrt{3}\,,\,-4\,)\,\)
\(\,2\,\)次関数\(\,y=x^2\,\)のグラフの頂点は
\(\,(\,0\,,\,0\,)\,\)
なので\(\,G\,\)は\(\,2\,\)次関数\(\,y=x^2\,\)を
\(\,x\,\)軸方向に\(\,\color{black}{\fbox{ 3 }}+\sqrt{\color{black}{\fbox{ 3 }}}\,\)
\(\,y\,\)軸方向に\(\,\color{black}{\fbox{ －4 }}\,\)
だけ平行移動したものであることが分かります。
ネ \(\,\underline{ 3 }\,\) ノ \(\,\underline{ 3 }\,\) ハヒ \(\,\underline{ -4 }\,\)
放物線の平行移動は頂点の移動を見れば良いのです。
また\(\,G\,\)と\(\,y\,\)軸との交点は\(\,x=0\,\)のときなので、
\(\begin{eqnarray}
f(0)&=&(3+\sqrt{3})^2-4\\
&=&9+6\sqrt{3}+3-4\\
&=&8+6\sqrt{3}
\end{eqnarray}\)
から求める\(\,y\,\)座標は
\(\,\color{black}{\fbox{ 8 }}+\color{black}{\fbox{ 6 }}\sqrt{\color{black}{\fbox{ 3 }}}\,\)
フ \(\,\underline{ 8 }\,\) ヘ \(\,\underline{ 6 }\,\) ホ \(\,\underline{ 3 }\,\)
第\(\,1\,\)問はここまでです。
第\(\,2\,\)問は三角比とデータの活用です。
⇒ 2020年度センター試験数学1Ａ(第2問三角比とデータ)の解説
まとめページ
で全体を通して見ておいてください。
「昨年度と比べて」、とかではなく、きっちりと基本を抑えていれば難しい問題ではありません。