2020年(令和2年)度に行われたセンター試験数学1Aの第2問の解説です。
この問題も例年通り三角比(図形と計量)とデータの活用です。
三角比は図を書けば基本定理の利用のみです。
データの分析は用語の意味を理解していれば大した計算はありません。
センター試験2020年度数学\(\,\mathrm{ⅠA}\,\)の問題です。
第2問三角比とデータの分析
第\(\,2\,\)問は〔\(\,1\,\)〕が三角比(図形と計量)、〔\(\,2\,\)〕がデータの活用(分析)です。
〔1〕三角比の基本定理を利用する問題
長くなるので早速問題を解いていきましょう。
「\(\,\mathrm{△ABC}\,\)において」、って図がないでしょう?
図を書きましょう。正確で無くて良いのでおおよそ長さの比が合うように描ければ十分です。
\(\,\mathrm{BC=2\sqrt{2}}\,\)
\(\,\mathrm{CD}\,\)は\(\,\mathrm{∠ACB}\,\)の二等分線
\(\,\mathrm{CD=\sqrt{2}}\,\)
\(\,\mathrm{\cos \angle{BCD}=\displaystyle \frac{3}{4}}\,\)
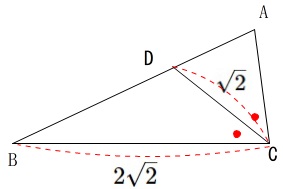 余弦定理から
余弦定理から
\(\begin{eqnarray}\displaystyle
\mathrm{BD^2}&=&\mathrm{BC^2+DC^2-2BC\cdot DC\cos \angle{BCD}}\\
&=&(2\sqrt{2})^2+(\sqrt{2})^2-2\cdot 2\sqrt{2}\cdot \sqrt{2}\cdot \frac{3}{4}\\
&=&8+2-6\\
&=&4
\end{eqnarray}\)
長さなので\(\,\mathrm{BD>0}\,\)だから
\(\,\mathrm{BD}=\color{black}{\fbox{ 2 }}\,\)
ア \(\,\underline{ 2 }\,\)
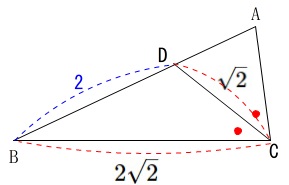 \(\,\mathrm{∠ADC=180°-∠BDC}\,\)
\(\,\mathrm{∠ADC=180°-∠BDC}\,\)
なので
\(\begin{eqnarray}
\color{red}{\sin \angle{\mathrm{ADC}}}&=&\color{magenta}{\sin \angle{\mathrm{BDC}}}\\
\end{eqnarray}\)
正弦定理を使った場合
\(\,3\,\)辺が分かっているので余弦定理で良いのですが、
正弦定理を使っていないので、正弦定理を使った場合の解法です。
問題全体を見渡せば後で正弦定理を使うのでここは余弦定理で良いのですが、、、
正弦定理を使ってしまったとしても答えは出ます。
\(\cos \angle{\mathrm{BCD}}=\displaystyle \color{red}{\frac{3}{4}}\)
より
\(\begin{eqnarray}\displaystyle
\sin^2 \angle{\mathrm{BCD}}&=&1-\cos^2 \angle{\mathrm{BCD}}\\
&=&1-\left(\color{red}{\frac{3}{4}}\right)^2\\
&=&1-\frac{9}{16}\\
&=&\frac{7}{16}
\end{eqnarray}\)
\(\,\mathrm{∠BCD}\,\)は三角形の内角なので\(\,\mathrm{\sin \angle{BCD}>0}\,\)だから
\(\color{blue}{\sin \angle{\mathrm{BCD}}}=\displaystyle \color{blue}{\frac{\sqrt{7}}{4}}\)
正弦定理から
\(\begin{eqnarray}\displaystyle
\frac{2}{\sin \angle{\mathrm{BCD}}}&=&\frac{2\sqrt{2}}{\sin \angle{\mathrm{BDC}}}\\
2\times \sin\angle{\mathrm{BDC}}&=&2\sqrt{2}\sin\angle{\mathrm{BCD}}\\
\color{magenta}{\sin \angle{\mathrm{BDC}}}&=&\sqrt{2}\times \color{blue}{\sin\angle{\mathrm{BCD}}}\\
\color{red}{\sin \angle{\mathrm{ADC}}}&=&\sqrt{2}\times \color{blue}{\frac{\sqrt{7}}{4}}\\
&=&\frac{\sqrt{\color{black}{\fbox{ 14 }}}}{\color{black}{\fbox{ 4 }}}
\end{eqnarray}\)
イウ \(\,\underline{ 14 }\,\) エ \(\,\underline{ 4 }\,\)
余弦定理を使った場合
余弦定理から\(\,\mathrm{\cos \angle{\mathrm{BDC}}}\,\)を求めて、
\(\,\mathrm{\cos \angle{\mathrm{ADC}}=-\cos \angle{\mathrm{BDC}}}\,\)
から
\(\sin^2 \angle{\mathrm{ADC}}+\cos^2 \angle{\mathrm{ADC}}=1\)
を利用しても答えは同じです。
\(\begin{eqnarray}\displaystyle
\cos \angle{\mathrm{BDC}}&=&\frac{(2)^2+(\sqrt{2})^2-(2\sqrt{2})^2}{2\cdot 2\cdot \sqrt{2}}\\
&=&\frac{4+2-8}{4\sqrt{2}}\\
&=&\color{red}{-\frac{1}{2\sqrt{2}}}
\end{eqnarray}\)
(\(\mathrm{∠BDC}\,\)は鈍角です。)
このことから
\(\begin{eqnarray}\displaystyle
\sin \angle{\mathrm{BDC}}&=&\sin \angle{\mathrm{ADC}}\\
&=&\sqrt{1-\left(-\frac{1}{2\sqrt{2}}\right)^2}\\
&=&\sqrt{\frac{7}{8}}\\
&=&\frac{\sqrt{7}}{2\sqrt{2}}\\
&=&\frac{\sqrt{14}}{4}
\end{eqnarray}\)
どちらでも同じような計算量ですけど、
\(\mathrm{∠BDC}\,\)が鈍角(\(\,\mathrm{∠ADC}\,\)が鋭角)だと分かるので、
後で\(\,\mathrm{AD}\,\)を求めるとき楽になります。
じゃあ、なんで正弦定理を優先したか?
悩んでいるヒマがあれば突っ走った方がはやいからです。
次に、\(\displaystyle \frac{\mathrm{AC}}{\mathrm{AD}}\)です。
問題にある二等分線の条件を利用していません。
角の二等分線定理から
\(\begin{eqnarray}\displaystyle
\mathrm{BC:AC}&=&\mathrm{BD:AD}\\
2\sqrt{2}:\mathrm{AC}&=&2:\mathrm{AD}\\
2\mathrm{AC}&=&2\sqrt{2}\mathrm{AD}\\
\mathrm{\frac{AC}{AD}}&=&\sqrt{\color{black}{\fbox{ 2 }}}
\end{eqnarray}\)
オ \(\,\underline{ 2 }\,\)
このとき\(\,\mathrm{AD}=\color{red}{x}\,\)とおくと\(\,\mathrm{AC}=\color{red}{\sqrt{2}x}\,\)です。
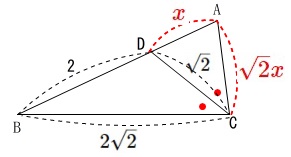 \(\,\mathrm{△ADC}\,\)に余弦定理を用いると\(\,x\,\)が求まります。
\(\,\mathrm{△ADC}\,\)に余弦定理を用いると\(\,x\,\)が求まります。
∠ACDを余弦定理に使った場合
余弦定理から
\(\begin{eqnarray}
x^2&=&(\sqrt{2})^2+(\sqrt{2}x)^2-2\cdot \sqrt{2}\cdot \sqrt{2}x\cdot \cos \angle{\mathrm{ACD}}\\
&=&2+2x^2-4x\cdot \frac{3}{4}\\
&=&2x^2-3x+2
\end{eqnarray}\)
これから
\(\begin{eqnarray}
x^2-3x+2&=&0\\
(x-1)(x-2)&=&0\\
x&=&1\,,\,2
\end{eqnarray}\)
\(\,\mathrm{AD=1}\,\)または\(\,\mathrm{AD=2}\,\)です。
図を描くとき線分比をおおよそ合わせていれば\(\,\mathrm{AD=1}\,\)だと判断できますが、
\(\,\mathrm{AD=2}\,\)のとき\(\,\mathrm{△CDB}\,\)≡\(\,\mathrm{△CDA}\,\)となるのでダメなことは分かります。
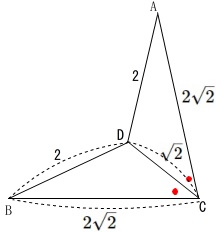 確認しておきます。
確認しておきます。
\(\,\mathrm{AD=1}\,\)のとき
\(\begin{eqnarray}\displaystyle
\cos \angle{\mathrm{ADC}}&=&\frac{1^2+(\sqrt{2})^2-(\sqrt{2})^2}{2\cdot 1\cdot \sqrt{2}}\\
&=&\frac{1+2-2}{4}\\
&=&\frac{1}{4}
\end{eqnarray}\)
これは\(\,\mathrm{∠ADC}\,\)が鋭角であることに適しています。
(\(\,\mathrm{∠BDC}\,\)が鈍角だから。)
\(\,\mathrm{AD=2}\,\)のとき
\(\begin{eqnarray}\displaystyle
\cos \angle{\mathrm{ADC}}&=&\frac{2^2+(\sqrt{2})^2-(2\sqrt{2})^2}{2\cdot 2\cdot \sqrt{2}}\\
&=&\frac{4+2-8}{4\sqrt{2}}\\
&=&-\frac{1}{2\sqrt{2}}
\end{eqnarray}\)
(\(\,\mathrm{\cos \angle{BDC}}\,\)と同じです。\(\,\mathrm{∠ADC}\,\)が鈍角となるので不適。)
よって、
\(\,\mathrm{AD}=\color{black}{\fbox{ 1 }}\,\)
∠ADCを余弦定理に使った場合
余弦定理から
\(\,\displaystyle \mathrm{\cos \angle{BDC}=-\frac{1}{2\sqrt{2}}}\,\)
と分かれば、
\(\,\color{red}{\cos (180^{\circ}-\theta)=-\cos \theta}\,\)
だから
\(\,\displaystyle \mathrm{\cos \angle{ADC}=\frac{1}{2\sqrt{2}}}\,\)
なので、\(\,\mathrm{△ADC}\,\)に余弦定理を用いて
\(\begin{eqnarray}\displaystyle
\mathrm{AC^2}&=&\mathrm{AD^2+DC^2-2AD\cdot DC\cdot \cos \angle{ADC}}\\
(\sqrt{2}x)^2&=&x^2+(\sqrt{2})^2-2\cdot \sqrt{2}\cdot x\cdot \frac{1}{2\sqrt{2}}\\
2x^2&=&x^2+2-x\\
x^2+x-2&=&0\\
(x-1)(x+2)&=&0
\end{eqnarray}\)
なので
\(\,x=\mathrm{AD}=1\,\)
と答えは1つに絞られます。
(こっちが模範解答になるでしょうけど、思いついた方法で突き進んでも十分時間はあります。)
外接円の半径は正弦定理です。
倍角の公式から
\(\begin{eqnarray}\displaystyle
\sin \angle{\mathrm{ACB}}&=&\sin 2\angle{\mathrm{BCD}}\\
&=&2\sin \angle{\mathrm{BCD}}\cdot \cos \angle{\mathrm{BCD}}\\
&=&2\cdot \frac{\sqrt{7}}{4}\cdot \frac{3}{4}\\
&=&\frac{3\sqrt{7}}{8}
\end{eqnarray}\)
よって、正弦定理から
\(\begin{eqnarray}\displaystyle
\frac{\mathrm{\color{red}{AB}}}{\color{blue}{\sin \angle{\mathrm{ACB}}}}&=&2R\\
R&=&\frac{\color{red}{AB}}{2\color{blue}{\sin \angle{ACB}}}\\
&=&\frac{\color{red}{3}}{2\times \color{blue}{\frac{3\sqrt{7}}{8}}}\\
&=&3\times \frac{4}{3\sqrt{7}}\\
&=&\frac{4\sqrt{7}}{7}
\end{eqnarray}\)
と出せます(出したい?)が\(\,\mathrm{ⅠA}\,\)の問題なので、
\(\begin{eqnarray}\displaystyle
\cos \angle{\mathrm{ACB}}&=&\frac{(2\sqrt{2})^2+(\sqrt{2})^2-3^2}{2\cdot 2\sqrt{2}\cdot \sqrt{2}}\\
&=&\frac{8+2-9}{8}\\
&=&\frac{1}{8}
\end{eqnarray}\)
このとき
\(\begin{eqnarray}\displaystyle
\sin \angle{\mathrm{ACB}}&=&\sqrt{1-\left(\frac{1}{8}\right)^2}\\
&=&\frac{3\sqrt{7}}{8}
\end{eqnarray}\)
正弦定理
\(\displaystyle \frac{\mathrm{AB}}{\sin \angle{\mathrm{ACB}}}=2R\)
から
\(\begin{eqnarray}\displaystyle
R&=&\frac{3}{2\sin \angle{ACB}}\\
&=&\frac{3}{2\times \frac{3\sqrt{7}}{8}}\\
&=&3\times \frac{4}{3\sqrt{7}}\\
&=&\frac{\color{black}{\fbox{ 4 }}\sqrt{\color{black}{\fbox{ 7 }}}}{\color{black}{\fbox{ 7 }}}
\end{eqnarray}\)
キ \(\,\underline{ 4 }\,\) ク \(\,\underline{ 7 }\,\) ケ \(\,\underline{ 7 }\,\)
深く考えずにゴリゴリ計算を進めていけば基本定理だけで終わります。
ここではいろいろと説明していますが、
実際の試験で取る解法はどれか1つで良いのでそれほど時間はかかりませんよ。
〔2〕データの活用(箱ひげ図と度数分布表)
表や図からデータを読み取る問題です。
(1)四分位数の意味
(1)
\(\,99\,\)個のデータの代表値と四分位数に関する問題です。
選択肢が多いですが「どのようなデータでも成り立つ」ものを探すので、
成り立たないものを用意できるか、を見ていけばすぐに終わります。
先に、データを四分割するのが何番目のデータなのか見ておきます。
\(\,99\,\)個のデータを小さい順に\(\,\color{red}{1}\,\)~\(\,\color{red}{99}\,\)とします。
赤字は番目であって値ではありませんよ。
四分位数を決めるのは「何番目にあるか」ですが、四分位数はその値です。
\(\,99\,\)個のデータの中央値は\(\,\color{red}{50}\,\)番目の\(\color{blue}{\fbox{値}}\)です。
中央値\(\,\mathrm{Q_2}\,\) \(\,49\,\)個 | \(\color{blue}{\fbox{\(\,\color{red}{50}\,\)}}\) | \(\,49\,\)個
左の小さい方のデータ\(\,49\,\)個の中央値が第\(\,1\,\)四分位数になります。
第\(\,1\,\)四分位数\(\,\mathrm{Q_1}\,\) \(\,24\,\)個 | \(\color{blue}{\fbox{\(\,\color{red}{25}\,\)}}\) | \(\,24\,\)個
右の大きい方のデータ\(\,49\,\)個の中央値が第\(\,3\,\)四分位数です。
第\(\,3\,\)四分位数\(\,\mathrm{Q_3}\,\) \(\,24\,\)個 | \(\color{blue}{\fbox{\(\,\color{red}{75}\,\)}}\) | \(\,24\,\)個
全体を並べると
\(\,24\,\)個 \(\color{blue}{\fbox{\(\,\color{red}{25}\,\)}}\) \(\,24\,\)個 \(\color{blue}{\fbox{\(\,\color{red}{50}\,\)}}\) \(\,24\,\)個 \(\color{blue}{\fbox{\(\,\color{red}{75}\,\)}}\) \(\,24\,\)個
 これが理解できていないとデータの活用は、箱ひげ図は利用できません。
これが理解できていないとデータの活用は、箱ひげ図は利用できません。
「箱ひげ図」は新課程では中学校の内容になります。
⓪「平均値は第\(\,1\,\)四分位数と第\(\,3\,\)四分位数の間にある。」
例えば、
\(\,\color{red}{1}\,\)~\(\,\color{red}{98}\,\)までの値が\(\,\color{blue}{0}\,\)で、
\(\,\color{red}{99}\,\)の値が\(\,\color{blue}{990}\,\)だとすると、
平均値は\(\displaystyle \frac{990}{99}=\color{magenta}{10}\,\)ですが
第\(\,1\,\)四分位数も第\(\,3\,\)四分位数も\(\,0\,\)です。
間はすべて\(\,0\,\)なので成り立ちません。
①「四分位範囲は標準偏差より大きい。」
上の⓪とデータと同じだとすると四分位範囲は\(\,0\,\)です。
標準偏差は\(\,0\,\)ではないので四分位範囲が大きいということは成り立ちません。
②「中央値より小さい観測値は\(\,49\,\)個である。」
上の⓪のデータだとすると中央値は\(\,0\,\)ですが、
中央値より小さい観測値はありません。
③「最大値に等しい観測地を\(\,1\,\)個削除しても四分位範囲は変わらない。」
四分位範囲は\(\,\mathrm{Q_3-Q_1}\,\)なので\(\,99\,\)個のデータの
\(\,(\color{red}{75}の値)-(\color{red}{25}の値)\,\)
です。
最大値となるデータを1つ削除すると\(\,98\,\)個のデータになります。
このとき、
中央値は\(\,\color{red}{49}\,\)と\(\,\color{red}{50}\,\)の平均値
第\(\,1\,\)四分位数\(\,\mathrm{Q_1}\,\)は\(\,\color{red}{25}\,\)の値
第\(\,3\,\)四分位数\(\,\mathrm{Q_3}\,\)は\(\,\color{red}{75}\,\)の値
なので、四分位範囲\(\,\mathrm{Q_3-Q_1}\,\)は
\(\,(\color{red}{75}の値)-(\color{red}{25}の値)\,\)
となるので四分位範囲は変わりません。\(\,○\,\)
④「第\(\,1\,\)四分位数より小さい観測値と、第\(\,3\,\)四分位より大きい観測値とをすべて削除すると、残りの観測値の個数は\(\,51\,\)個である。
上の⓪で例えたデータにおいて、この条件でデータを削除すると、
第\(\,1\,\)四分位数は\(\,0\,\)、第\(\,3\,\)四分位数も\(\,0\,\)なので、観測値は\(\,0\,\)個になります。
成り立ちません。
残るのは⑤だけなので⑤は答えの1つですが、確認しておきます。
⑤
⓪で作ったデータでも分かりますが、
「第\(\,1\,\)四分位数\(\,\color{red}{より}\,\)小さい観測値」
「第\(\,3\,\)四分位数\(\,\color{red}{より}\,\)大きい観測値」
を削除するので、
元のデータの\(\,\mathrm{Q_1}\,\)が最小値、\(\,\mathrm{Q_3}\,\)が最大値
となります。
よって、
削除したデータの最大値と最小値の差である「範囲」
と、
元のデータの「四分位範囲」\(\,(\mathrm{Q_3-Q1})\,\)は同じ値
となります。\(\,○\,\)
コ \(\,\underline{ ③ }\,\) サ \(\,\underline{ ⑤ }\,\)
データについて計算はまだ何もしていません。
分かり易くするため平均値を1つ計算しましたがしなくても分かることです。
箱ひげ図の読み取り
(2)
(\(\,Ⅰ\,\))(\(\,Ⅱ\,\))(\(\,Ⅲ\,\))の正誤を見ます。
(\(\,Ⅰ\,\))「四分位範囲はどの都道府県においても\(\,1\,\)以下である。」
四分位範囲は箱ひげ図において長方形の幅なので、
\(\,\mathrm{P10}\,\)では明らかに\(\,1\,\)を超えているので間違いです。
(\(\,Ⅱ\,\))「中央値が小さい順に上から並んでいる。」
中央値は箱ひげ図の長方形の中にある太線のことなので、
\(\,\mathrm{P7}\,\)と\(\,\mathrm{P8}\,\)や\(\,\mathrm{P10}\,\)と\(\,\mathrm{P11}\,\)は逆になっていますので間違いです。
(\(\,Ⅲ\,\))「\(\,\mathrm{P1}\,\)のデータのどの値と\(\,\mathrm{P47}\,\)のどの値とを比較しても\(\,1.5\,\)以上の差がある。」
\(\,\mathrm{P1}\,\)の最大値は\(\,79.5\,\)より小さい
\(\,\mathrm{P47}\,\)の最小値は\(\,\mathrm{81.0}\,\)より大きい
ので、どの値を比較しても差は
少なくとも\(\,1.5\,\)以上
あります。正しい。
(\(\,Ⅰ\,\))誤 (\(\,Ⅱ\,\))誤 (\(\,Ⅲ\,\))正
シ \(\,\underline{ ⑥ }\,\)
度数分布表と箱ひげ図の関係
(3)
ある都道府県の\(\,20\,\)市町村の平均寿命のデータです。
\(\,20\,\)市町村あるのは佐賀県ですが、関係ありません。笑
階級は区間が「左が以上、右が未満」と普通に分けられていることをわざわざ説明してくれています。
度数分布表にすると分かり易いので書いておきます。
(ヒストグラムに度数を書き込めば必要ないですよ。)
第\(\,1\,\)四分位数\(\,\mathrm{Q_1}\,\)は小さい方から\(\,\color{blue}{5,6}\,\)番目の平均
中央値\(\,\mathrm{Q_2}\,\)は小さい方から\(\,\color{red}{10,11}\,\)番目の平均
第3四分位数\(\,\mathrm{Q_3}\,\)は小さい方から\(\,\color{magenta}{15,16}\,\)番目の平均
(累積度数で見れば良いです。)
なのでどの階級にあるか度数分布表に示しておきます。
\(\begin{array}{|c|c|c|} \hline
平均寿命 & 度数 & 累積度数 \\ \hline
7.95~80.0 & 2 & \\ \hline
80.0~80.5 & 4 & \color{blue}{6}\,\mathrm{\color{blue}{Q_1}} \\ \hline
80.5~81.0 & 9 & \color{red}{15}(\color{magenta}{15})\,\mathrm{\color{red}{Q_2}},\mathrm{\color{magenta}{Q_3}} \\ \hline
81.0~81.5 & 3 & \color{magenta}{18}\,\mathrm{\color{magenta}{Q_3}} \\ \hline
81.5~82.0 & 2 & 20 \\ \hline
\end{array}\)
箱ひげ図を大まかに説明すると
最小値\(\,\mathrm{Q_0}\,\)は\(\,7.95~80.0\,\)の階級
第\(\,1\,\)四分位数\(\,\mathrm{Q_1}\,\)は\(\,\color{blue}{80.0~80.5}\,\)の階級
中央値\(\,\mathrm{Q_2}\,\)は\(\,\color{red}{80.5~81.0}\,\)の階級
第\(\,3\,\)四分位数は\(\,\color{magenta}{80.5~81.0}\,\)または\(\,\color{magenta}{81.0~81.5}\,\)の階級
最大値\(\,\mathrm{Q_4}\,\)は\(\,81.5~82.0\,\)の階級
となります。

最小値から①②⑥⑦はなくなります。
第\(\,1\,\)四分位数から⓪⑤はなくなります。
中央値は③④どちらもあり得ます。
第\(\,3\,\)四分位数はどちらもあり得ます。
最大値から③はなくなります。
ス \(\,\underline{ ④ }\,\)
まだ計算はしていません。
散布図の読み取り
(4)
図\(\,3\,\)は「都道府県別の男の平均寿命と女の平均寿命」を散布図として記してあります。
例えば、
一番左下の都道府県を示す\(\,○\,\)は、
男の平均寿命\(\,78.7\,\)歳
女の平均寿命\(\,85.9\,\)歳
平均寿命の差が\(\,85.9-78.7\,=\,7.2\,\)くらい
ということです。
「男の平均寿命」を\(\,x\,\)座標、「女の平均寿命」を\(\,y\,\)座標として点を打っているということです。
傾き\(\,1\,\)の直線が\(\,5\,\)本書かれています。
\(\,y\,\)切片は、「男の平均寿命」と「女の平均寿命」の『差』を意味します。
例えば、\(\,1\,\)番左の直線は、傾き\(\,1\,\)、切片\(\,7.5\,\)の直線です。
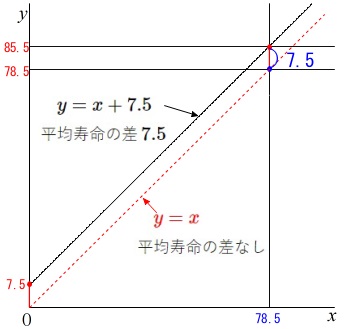 \(\color{red}{y=x}\)上の点は平均寿命の差なし
\(\color{red}{y=x}\)上の点は平均寿命の差なし
\(y=x+7.5\)上の点は平均寿命の差\(\,7.5\,\)
ということです。
これの一部を拡大したのが図\(\,3\,\)です。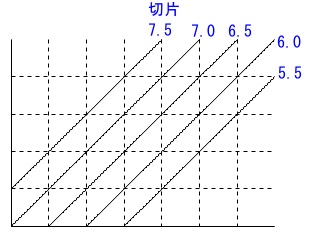 ここまで分かれば後は簡単に終わります。
ここまで分かれば後は簡単に終わります。
平均寿命の差が\(\,5.5\,\)から\(\,6.0\,\)の間に点が\(\,9\,\)個
平均寿命の差が\(\,7.0\,\)から\(\,7.5\,\)の間に点が\(\,3\,\)個
この点は度数を表しているので、一致する度数分布表は\(\,③\,\)しかありません。
セ \(\,\underline{ ③ }\,\)
何も計算せずにデータの「分析のみ」で終わりました。
数学\(\,\mathrm{ⅡB}\,\)の統計を背景にかなりの計算をさせようとしていた昨年度までと比べると、「分析」という本来の意図からすればこちらの方が面白いですよね。
で、何が分かったかというと、
女性の方が長生きだということです。
このデータによると、同じ都道府県であれば、
男性は、だいたい\(\,6\,\)歳から\(\,7\,\)歳年上の女性と一緒になれば、
同じくらいに人生を終える。
ということでしょうか。笑
いやいや、このデータでは見えてきませんが、過去に世界でも見たことのない高齢化社会になっている日本です。
ということで第\(\,2\,\)問はここまでです。
ここまでで配点が\(\,60\,\)点、平均点には届くはずですのでしっかり見直しておきましょう。
基本的なことができていないと平均点も取れないということです。
第\(\,3\,\)問は場合の数と確率です。
⇒ センター試験数学1A(2020年度)第3問場合の数と確率の解説
すみません、更新は定期的ではありません。
センター試験、共通テストの解説まとめページで確認して下さい。