2020年(令和2年)度センター試験数学2Bの第2問の解説です。
第2問は2つの放物線と共通接線に関する微分積分の問題です。
前半で共通接線を求め、後半で曲線が囲む面積と最大値を求めます。
\(\,2020\,\)年度センター試験数学\(\,\mathrm{ⅡB}\,\)の問題です。
第２問微分積分（２つの放物線と接線と囲む面積）
２つの放物線は\(\,2\,\)次関数なので平方完成しておおよその位置関係は見ておきましょう。
計算量は多いとは言えませんが、一つひとつしっかり計算しておかないと接線を一致させるときに苦労します。
条件を見ておきましょう。
\(\,a\,＞\,0\,\)
\(\,D:f(x)=x^2-(4a-2)x+4a^2+1\,\)
\(\,C:y=x^2+2x+1\,\)
\(\,\ell\,\)は\(\,\,C,D\,\,\)の共通接線
位置関係を見ておきたいので平方完成しておきます。
放物線\(\,C\,\)は
\(\begin{eqnarray}
y&=&x^2+2x+1\\
&=&(x+1)^2
\end{eqnarray}\)
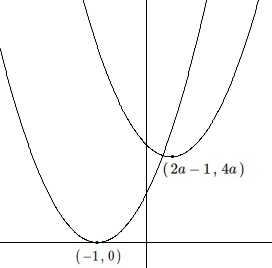
頂点は\(\,(\,-1\,,\,0\,)\,\)で固定されています。
また、放物線\(\,D\,\)は
\(\begin{eqnarray}
f(x)&=&x^2-(4a-2)x+4a^2+1\\
&=&x^-2(2a-1)x+4a^2+1\\
&=&\{x-(2a-1)\}^2-(2a-1)^2+4a^2+1\\
&=&\{x-(2a-1)\}^2+4a
\end{eqnarray}\)
頂点は\(\,(\,2a-1\,,\,4a\,)\,\)で、
\(\,a\,>\,0\,\)なので、放物線\(\,C\,\)よりは右上に位置しています。
（１）共通接線を求める
「\(\,\ell\,\)の方程式を求めよう。」
というのは、これから誘導してくれるという合図です。
接線と放物線\(\,C\,\)との接点を
\(\,(\,\color{blue}{t}\,,\,\color{blue}{t^2+2t+1}\,)\,\)
とすると
\(\,y’=2x+2\,\)
より\(\,x=\color{blue}{t}\,\)のときの接線の傾きは
\(\color{red}{2t+2}\)
なので接線の方程式は
\(\begin{eqnarray}
y-(\color{blue}{t^2+2t+1})&=&(\color{red}{2t+2})(x-\color{blue}{t})\\
&=&(2t+2)x-2t^2-2t
\end{eqnarray}\)
これを整理すると
\(\begin{eqnarray}
y&=&(2t+2)x-2t^2-2t+t^2+2t+1\\
&=&(\fbox{ 2 }t+\fbox{ 2 })x-t^2+\fbox{ 1 } ･･･①
\end{eqnarray}\)
また、\(\,D\,\)上の点
\(\,(\,\color{blue}{s}\,,\,\color{blue}{f(s)}\,)\,\)
における接線は、
\(y-(\color{blue}{f(s)})=f'(s)(x-\color{blue}{s})\)
\(\,f'(x)=2x-4a+2\,\)
なので、\(\,x=\color{blue}{s}\,\)における接線の傾きは
\(\,f'(s)=\color{red}{2s-4a+2}\,\)
さらに
\(\,f(\color{blue}{s})=\color{blue}{s^2-(4a-2)s+4a^2+1}\,\)
であることから接線の方程式は
\(y-(\color{blue}{s^2-(4a-2)s+4a^2+1})=(\color{red}{2s-4a+2})(x-\color{blue}{s})\)
これを整理すると
\(\begin{eqnarray}
y&=&(2s-4a+2)x-2s^2+4as-2s\\
&&\hspace{10pt}+s^2-(4a-2)s+4a^2+1\\
&=&(2s-4a+2)x-2s^2+\color{magenta}{4as-2s}\\
&&\hspace{10pt}+s^2\color{magenta}{-4as+2s}+4a^2+1\\
&=&(\,\fbox{ 2 }s-\fbox{ 4 }a+\fbox{ 2 }\,)x-s^2+\fbox{ 4 }a^2+\fbox{ 1 } ･･･②
\end{eqnarray}\)
2つの接線①②は同じ直線を表しているので傾きおよび\(\,y\,\)切片が一致するから
\( \begin{cases}
\hspace{7pt} 2t+2=2s-4a+2\\ \\
\hspace{7pt} -t^2+1=-s^2+4a+1
\end{cases}\)
\(\,t,s\,\)についての連立方程式なのでこれを解くと、
第\(\,1\,\)方程式から
\(t=s-2a\)
これを第\(\,2\,\)方程式に代入して
\(\,t=\fbox{ 0 }\,,\,s=\fbox{ 2 }a\,\)
よって、接線\(\,\ell\,\)は①か②から（①からの方がだんぜん楽）
\(y=\fbox{ 2 }x+\fbox{ 1 }\)
（２）曲線と軸で囲まれる面積の積分
先ずは2つの放物線\(\,C,D\,\)の交点を求めるので連立です。
\( \begin{cases}
\hspace{7pt} y=x^2+2x+1\\ \\
\hspace{7pt} y=x^2-(4a-2)x+4a^2+1
\end{cases}\)
から
\(x^2+2x+1=x^2-(4a-2)x+4a^2+1\)
これを解いて
\(\begin{eqnarray}
2x+1+(4a-2)x-1&=&0\\
4ax&=&4a^2\\
\end{eqnarray}\)
\(\,a\,＞\,0\,\)なので交点の\(\,x\,\)座標は
\(x=\fbox{ \(\,a\,\) }\)
これが積分区間の上限になります。
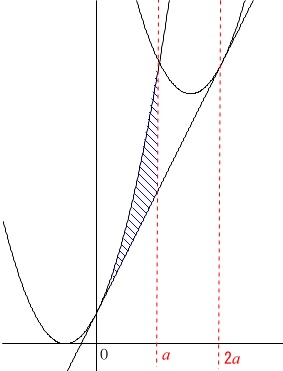よって、\(\,C\,\)と\(\,\ell\,\)および\(\,x=a\,\)によって囲まれた図形の面積\(\,S\,\)は
\(\begin{eqnarray}\displaystyle
S&=&\int_0^a (\,C-\ell\,) dx\\
&=&\int_0^a \{(x^2+2x+1)-(2x+1)\}dx\\
&=&\int_0^a x^2 \,dx\\
&=&\left[\,\frac{1}{3}x^3\,\right]_0^a\\
&=&\frac{a^\fbox{ 3 }}{\fbox{ 3 }}\,
\end{eqnarray}\)
（３）接点の違いによる一定区間の面積の値の変化
「\(\displaystyle \,a\,≧\,\frac{1}{2}\,\)とする。」
これは積分区間\(\,0\,≦\,x\,≦\,1\,\)が\(\,D\,\)との接点を超えない、ということです。
積分区間\(\,0\,≦\,x\,≦\,1\,\)より放物線の交点の\(\,x\,\)座標\(\,a\,\)が大きい値のとき
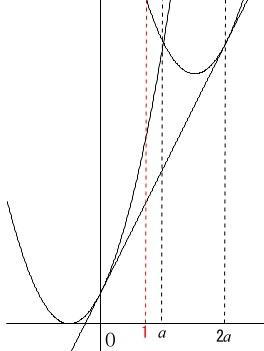つまり、\(\,a\,＞\,\fbox{ 1 }\,\)のとき
\(\begin{eqnarray}\displaystyle
T&=&\int_0^1 \{(x^2+2x+1)-(2x+1)\}\,dx\\
&=&\int_0^1 x^2\, dx\\
&=&\left[\,\frac{1}{3}\,x^3\,\right]_0^1\\
&=&\frac{\fbox{ 1 }}{\fbox{ 3 }}
\end{eqnarray}\)
次に、積分区間の上限\(\,1\,\)が、
放物線の交点の\(\,x\,\)座標\(\,a\,\)と\(\,D\,\)の接点の\(\,x\,\)座標\(\,2a\,\)の間にあるとき
\(\hspace{10pt}\,a\,≦\,1\,,\,1\,≦\,2a\,\)
つまり、
\(\hspace{10pt}\displaystyle \frac{1}{2}\,≦\,a\,≦\,1\)
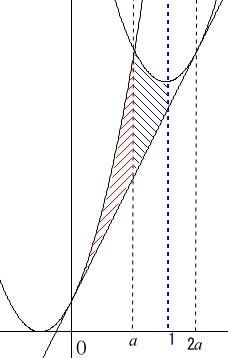のとき,
\(\begin{eqnarray}\displaystyle
T&=&\int_0^a (\,C-\ell\,)\,dx+\int_a^1 (\,D-\ell\,)\,dx\\
&=&\int_0^a x^2\,dx+\int_a^1 \{(\,x^2-(4a-2)x+4a^2+1\,)-(\,2x+1\,)\}dx\\
&=&\int_0^a x^2\,dx+\int_a^1 (\,x^2-4ax+4a^2\,)\,dx\\
&=&\left[\frac{1}{3}\,x^3\right]_0^a+\left[\,\frac{1}{3}x^3+2ax^2+4a^2x\,\right]_a^1\\
&=&\frac{1}{3}a^3+\left(\,\frac{1}{3}-2a+4a^2\,\right)-\left(\,\frac{1}{3}a^3-2a^2+4a^3\,\right)\\
&=&-\fbox{ 2 }a^3+\fbox{ 4 }a^2-\fbox{ 2 }a+\frac{\fbox{ 1 }}{\fbox{ 3 }}
\end{eqnarray}\)
この積分計算は、被積分関数が同じ部分があるので、
\(\begin{eqnarray}\displaystyle
T&=&\int_0^a x^2\,dx+\int_a^1 \{(\,x^2-(4a-2)x+4a^2+1\,)-(\,2x+1\,)\}dx\\
&=&\int_0^a \color{red}{x^2}\,dx+\int_a^1 (\,\color{red}{x^2}-4ax+4a^2\,)\,dx\\
&=&\int_0^1 x^2\,dx-\int_a^1 4ax\,dx+\int_a^1 4a^2\,dx\\
&=&\left[\,\frac{1}{3}x^3\,\right]_0^1-\left[\,2ax^2\,\right]_a^1+\left[\,4a^2x\,\right]_a^1\\
&=&\frac{1}{3}-(\,2a-2a^3\,)+(\,4a^2-4a^3\,)\\
&=&\frac{1}{3}-2a+2a^3+4a^2-4a^3\\
&=&-\fbox{ 2 }a^3+\fbox{ 4 }a^2-\fbox{ 2 }a+\frac{\fbox{ 1 }}{\fbox{ 3 }}
\end{eqnarray}\)
とした人もいるでしょう。どっちでも良いです。
ところで、ここまで誘導に乗って進んで来ただけで何も考えていないのですが、、、。
やったことと言えばグラフを書いて積分計算しただけ。
（４）３次関数の増減と最大値
ここまで出てきた値は\(\,\displaystyle \frac{1}{2}≦a≦1\,\)の範囲において
\(\hspace{10pt}\displaystyle S=\frac{a^3}{3}\)
および
\(\hspace{10pt}\displaystyle T=-2a^3+4a^2-2a+\frac{1}{3}\)
このとき
\(\begin{eqnarray}\displaystyle
U&=&2\,T-3\,S\\
&=&2\left(-2a^3+4a^2-2a+\frac{1}{3}\right)-3\left(\frac{a^3}{3}\right)\\
&=&-4a^3+8a^2-4a+\frac{2}{3}-a^3\\
&=&-5a^3+8a^2-4a+\frac{2}{3}
\end{eqnarray}\)
増減表ですね。
\(\begin{eqnarray}\displaystyle
U’&=&-15a^2+16a-4\\
&=&-(\,15a^2-16a+4\,)\\
&=&-(\,5a-2\,)(\,3a-2\,)
\end{eqnarray}\)
ここで
\((\,5a-2\,)(\,3a-2\,)=0\)
より
\(\hspace{10pt}\displaystyle a=\frac{2}{5}\,,\,\frac{2}{3}\)
増減表は
\(\,\begin{array}{c|c|c|c|c|c|c|}\displaystyle
a & \displaystyle \left(\frac{2}{5}\right)&\cdots & \displaystyle\frac{1}{2}& \cdots & \displaystyle\frac{2}{3} & \cdots & 1\\
\hline
U’ & 0 & + & & + & 0 & – &\\
\hline
U & 範囲外 & \nearrow & \color{red}{⇒} & \nearrow & 極大 & \searrow & \color{red}{\Leftarrow}
\end{array}\,\)
（\(\,\color{red}{⇒}\,\)と\(\,\color{red}{\Leftarrow}\,\)の間が定義域）
\(\hspace{10pt}\displaystyle \,a=\frac{\fbox{ 2 }}{\fbox{ 3 }}\,\)のとき極大かつ最大
となるので\(\,U\,\)に\(\displaystyle \,a=\frac{2}{3}\,\)を代入した最大値\(\,M\,\)は
\(\begin{eqnarray}\displaystyle
M&=&-5\left(\frac{2}{3}\right)^3+8\left(\frac{2}{3}\right)^2-4\left(\frac{2}{3}\right)+\frac{2}{3}\\
&=&-\frac{40}{27}+\frac{32}{9}-\frac{8}{3}+\frac{2}{3}\\
&=&\frac{-40+96-72+18}{27}\\
&=&\frac{\fbox{ 2 }}{\fbox{ 27 }}
\end{eqnarray}\)
少しは計算した気になれますね。笑
少し急いだので間違いがあればご指摘ください。
第\(\,3\,\)問は数列です。
パッと見た目には漸化式、\(\,\sum\,\)計算、一般項と類別？
微分積分よりは計算量が多いのでしょうか。
「求めよう。」があるので考えるより、手を動かした方がはやいです。
例年だと一番計算量、というか文字式を扱う量が多く思えるのが数列ですけどね。