2020年(令和2年)度センター試験数学2Bの第1問の解説です。
第1問は三角関数(方程式不等式)と指数対数関数(対称式交代式)の基本問題です。
三角関数では加法定理と合成、指数対数ではやはり定義がポイントになります。
\(\,2020\,\)年度センター試験数学\(\,\mathrm{ⅡB}\,\)の問題です。
いつも長くなるので、できるだけ簡単に、手短に説明しておきます。
くどくど説明するのはメンドクサイといえば確かにそうですが、
数学\(\,\mathrm{ⅡB}\,\)の得点率が低いのは基礎ができていないからなので、
ここの解説は傾向を知るということで、対策の補助として見ておいてください。
数学\(\,\mathrm{ⅠA\,,\,ⅡBの}\,\)要点は他のページでしてありますのでそちらで確認しておくと良いです。
⇒ 共通テスト(センター試験)数学の勉強法と対策まとめ単元別攻略と解説
第1問三角方程式不等式と指数対数の方程式不等式
三角関数の方程式や不等式を解く場合、
加法定理と合成は必ず使うと考えておかないと、他に方法がなくなります。笑
指数対数関数や方程式や不等式の場合は、他の分野同様定義が重要なポイントになります。
意識しなくとも使っていることが多いですが\(\,2020\,\)年はどうなっているのか、様子を見ながら進めましょう。
〔1〕三角関数の方程式と不等式
当然のことながら加法定理と合成ですが、
問題が誘導してくれているのでそのまま進めるだけで大丈夫です。
(1)加法定理と合成
\(\,0\,≦\,\theta\,<\,2\pi\)のとき
\(\displaystyle \sin \theta\,>\,\sqrt{3}\cos \left(\theta-\frac{\pi}{3}\right) ・・・①\)
この不等式を解けば良いのです。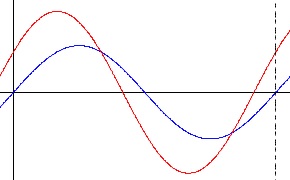 グラフの位置関係ですが交点の読み取りは簡単ではないでしょう。
グラフの位置関係ですが交点の読み取りは簡単ではないでしょう。
加法定理
\(\cos (\alpha-\beta)=\cos \alpha \cos \beta+\sin \alpha \sin \beta\)
を用いると、
\(\hspace{10pt}\displaystyle \sqrt{3}\cos \left(\theta-\frac{\pi}{3}\right)\\
\displaystyle =\sqrt{3}\left(\cos \theta\cdot \cos \frac{\pi}{3}+\sin \theta\cdot \sin \frac{\pi}{3}\right)\\
\displaystyle =\sqrt{3}\left(\cos \theta\cdot \frac{1}{2}+\sin \theta \cdot \frac{\sqrt{3}}{2}\right)\\
\displaystyle =\frac{\sqrt{\fbox{ 3 }}}{\fbox{ 2 }}\cos \theta+\frac{\fbox{ 3 }}{\fbox{ 2 }}\sin\theta\)
これは①の右辺なので、①は
\(\begin{eqnarray}\displaystyle
\sin \theta\,&>&\,\frac{\sqrt{3}}{2}\, \cos \theta+\frac{3}{2}\,\sin \theta\\
0\,&>&\,\frac{\sqrt{3}}{2}\,\cos \theta+\frac{1}{2}\,\sin\theta
\end{eqnarray}\)
この右辺を合成すると
\(\hspace{10pt}\displaystyle \sin \left(\theta+\frac{\pi}{3}\right)\,<\,0\)
\(\sin \mathrm{A}\,<\,0\,\)となるのは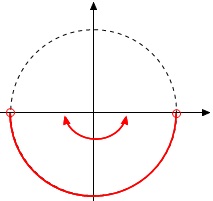
\(\hspace{10pt}\pi \,<\,A\,<\,2\pi\)
のときで、
\(\hspace{10pt}0\,≦\,\theta\,<\,2\pi\)
なので
\(\hspace{10pt}\displaystyle \frac{\pi}{3}\,≦\,\color{blue}{\theta+\frac{\pi}{3}}\,<\,\frac{7\pi}{3}\)
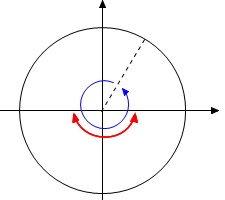 よって、不等式①を満たす\(\displaystyle \,\theta+\frac{\pi}{3}\,\)の範囲は1つで、
よって、不等式①を満たす\(\displaystyle \,\theta+\frac{\pi}{3}\,\)の範囲は1つで、
\(\begin{eqnarray}\displaystyle
\pi\,<\,\theta+\frac{\pi}{3}\,<\,2\pi\\
\Leftrightarrow \hspace{10pt}\frac{\fbox{ 2 }}{\fbox{ 3 }}\,\pi\,<\,\theta\,<\,\frac{\fbox{ 5 }}{\fbox{ 3 }}\,\pi
\end{eqnarray}\)
(2)三角比と2次方程式の解と係数の関係
\(\,2\,\)次方程式の解と係数の関係の問題です。
\(\hspace{10pt} 25x^2-35x+k=0\)
の解が\(\,\color{red}{\sin \theta}\,\)と\(\,\color{blue}{\cos \theta}\,\)です。
このとき解と係数の関係により
\( \begin{cases}
\hspace{7pt} \displaystyle \color{red}{\sin\theta}+\color{blue}{\cos \theta}=\frac{35}{25}=\frac{7}{5} ・・・①\\ \\
\hspace{7pt} \displaystyle \color{red}{\sin \theta} \color{blue}{\cos \theta}=\frac{k}{25} ・・・②
\end{cases}\)
ただし、
\(\displaystyle 0\,≦\,\theta\,≦\,\frac{\pi}{2}\)
なので
\(\begin{eqnarray}
0\,≦\,&\sin \theta&\,≦\,1\\
0\,≦\,&\cos \theta&\,≦\,1
\end{eqnarray}\)
の範囲で存在します。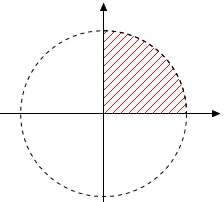 ①の両辺を\(\,2\,\)乗すると、
①の両辺を\(\,2\,\)乗すると、
\(\begin{eqnarray}\displaystyle
(\,\color{red}{\sin\theta}+\color{blue}{\cos \theta}\,)^2&=&\left(\,\frac{7}{5}\,\right)^2\\
1+2\color{red}{\sin \theta} \color{blue}{\cos \theta}&=&\frac{49}{25}\\
2\color{red}{\sin \theta} \color{blue}{\cos \theta}&=&\frac{49}{25}-1=\frac{24}{25}\\
\color{red}{\sin \theta} \color{blue}{\cos \theta}&=&\frac{12}{25}
\end{eqnarray}\)
これと②から
\(\begin{eqnarray}\displaystyle
\frac{k}{25}&=&\frac{12}{25}\\
∴ k&=&\fbox{ 12 }
\end{eqnarray}\)
このとき元の\(\,2\,\)次方程式は
\(\begin{eqnarray}\displaystyle
25x^2+35x+12&=&0\\
(\,5x-3\,)(\,5x-4\,)&=&0\\
x&=&\frac{3}{5}\,,\,\frac{4}{5}
\end{eqnarray}\)
\(\sin \theta\,≧\,\cos \theta\,\)とすると
\(\hspace{10pt}\displaystyle \color{red}{\sin \theta}=\frac{\fbox{ 4 }}{\fbox{ 5 }}\,,\,\color{blue}{\cos \theta}=\frac{\fbox{ 3 }}{\fbox{ 5 }}\)
第\(\,1\,\)象限で、
(単位円周上で\(\,(\,\color{blue}{\cos \theta}\,,\,\color{red}{\sin \theta}\,)\,\)を見ます。)
\(\displaystyle \,\sin\theta=\frac{4}{5}\,=\,0.8\,\)の場合、
\(\displaystyle \color{red}{\frac{1}{\sqrt{2}}}\,<\,0.8\,<\,\color{red}{\frac{\sqrt{3}}{2}}\)
または
\(\displaystyle \,\cos\theta=\frac{3}{5}\,=\,0.6\,\)の場合、
\(\displaystyle \color{blue}{\frac{1}{2}}\,<\,0.6\,<\,\color{blue}{\frac{1}{\sqrt{2}}}\)
を満たす\(\,\theta\,\)は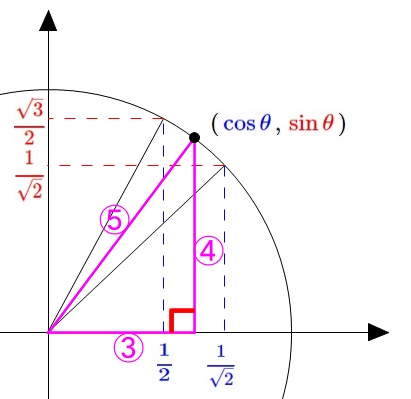 \(\hspace{10pt}\displaystyle \frac{\pi}{4}\,<\,\theta\,<\,\frac{\pi}{3}\)
\(\hspace{10pt}\displaystyle \frac{\pi}{4}\,<\,\theta\,<\,\frac{\pi}{3}\)
の範囲にあります。
単位円での\(\,x\,\)座標は\(\,\cos \theta\,\)、\(\,y\,\)座標は\(\,\sin \theta\,\)になります。
\(\hspace{10pt}\displaystyle \frac{1}{\sqrt{2}}=\frac{\sqrt{2}}{2}≒0.7・・・\)
\(\hspace{10pt}\displaystyle \frac{\sqrt{3}}{2}≒0.8・・・\)
より
\(\begin{eqnarray}\displaystyle
\frac{1}{\sqrt{2}}\,<\,&\color{red}{0.8}&\,<\,\frac{\sqrt{3}}{2}\\
\sin \frac{\pi}{4}\,<\,&\color{red}{\sin \theta}&\,<\,\sin \frac{\pi}{3}\\
\frac{\pi}{4}\,<\,&\theta&\,<\,\frac{\pi}{3}
\end{eqnarray}\)
\(\,x\,\)座標の\(\,\cos \theta\,\)で見ても同じように\(\,\theta\,\)の範囲は出せますのでやってみてください。
答え \(\,\underline{ ③ }\,\)
選択肢の範囲に等号が付いていますが、「または」の「\(\,=\,\)」なので付いていても問題ありません。
〔2〕指数対数関数の方程式と不等式
指数が分数の方程式は置換すれば見やすくなります。
対数の連立不等式は誘導されているので置換された文字について解いていけば問題ありませんね。
(1)対称式と交代式の計算問題
底は正の実数です。
\(\hspace{10pt}\displaystyle t^{\frac{1}{3}}-t^{-\frac{1}{3}}=-3\)
このままだと見にくいかもしれないので、
\(\hspace{10pt}\displaystyle t^{\frac{1}{3}}=a\,,\,t^{-\frac{1}{3}}=a^{-1}\)
と置きかえると
\(\color{red}{a-a^{-1}}=-3\)
このとき
\(\displaystyle t^{\frac{2}{3}}+t^{-\frac{2}{3}}\\
=\color{blue}{a^2+a^{-2}}\\
=(\color{red}{a-a^{-1}})^2+2a\cdot a^{-1}\\
=(\color{red}{a-a^{-1}})^2+2\\
=(-3)^2+2\\
=\fbox{ 11 }\)
指数のままだとわかりにくいという人は少し慣れた方が良いですが、
\(\displaystyle \,a^{-1}=\frac{1}{a}\,\)なので分数にすると
\(\displaystyle a-\frac{1}{a}=-3\)
このとき
\(\displaystyle t^{\frac{2}{3}}+t^{-\frac{2}{3}}\\
\displaystyle =a^2+\frac{1}{a^2}\\
\displaystyle =\left(a-\frac{1}{a}\right)^2+2a\cdot \frac{1}{a}\\
\displaystyle =\left(a-\frac{1}{a}\right)^2+2\\
=(-3)^2+2\\
=\fbox{ 11 }\)
また、
\(\hspace{10pt}\displaystyle (a+a^{-1})^2\\
=\color{blue}{a^2}+2a\cdot a^{-1}+\color{blue}{a^{-2}}\\
=\color{blue}{a^2+a^{-2}}+2\\
=11+2\\
=13\)
なので\(\,a+a^{-1}\,>\,0\,\)だから
\(\hspace{10pt}a+a^{-1}\\
\displaystyle =t^{\frac{1}{3}}+t^{-\frac{1}{3}}\\
\displaystyle =\sqrt{\fbox{ 13 }}\)
対称式、交代式で一度\(\,2\,\)乗するというのは普通ですね。
さらに、\(\,t=a^3\,\)なので
\(\hspace{10pt}t-t^{-1}\\
=a^3-a^{-3}\\
=(\color{red}{a-a^{-1}})(\color{blue}{a^2}+a\cdot a^{-1}+\color{blue}{a^{-2}})\\
=\color{red}{(a-a^{-1}})(\color{blue}{a^2+a^{-2}}+1)\\
=(\color{red}{-3})(\color{blue}{11}+1)\\
=\fbox{ -36 }\)
ここまでは普通に数学\(\,Ⅰ\,\)の基礎があれば問題ないでしょう。
対数と連立不等式
連立不等式①②を見ると底がそろっていません。
底をそろえておきましょう。
②は底が\(\,3\,\)のままで良いですが、真数のかけ算は対数の足し算なので、
\(\begin{eqnarray}
\log_{3}(x\sqrt{y})&≦&5\\
\log_{3}x+\log_{3}\sqrt{y}&≦&5\\
\log_{3}x+\log_{3}y^{\frac{1}{2}}&≦&5\\
\log_{3}+\frac{1}{2}\,\log_{3}y&≦&5 ・・・②’
\end{eqnarray}\)
③は底を②と同じ\(\,3\,\)にそろえるため底の変換公式を使います。
真数の割り算は対数の引き算になるのは①と同じことです。
\(\begin{eqnarray}
\log_{81}\frac{y}{x^3}&≦&1\\
\frac{\log_{3}\frac{y}{x^3}}{\log_{3}81}&≦&1\\
\log_{3}\frac{y}{x^3}&≦&\log_{3}81\\
\log_{3}y-\log{3}x^3&≦&\log_{3}3^4\\
\log_{3}y-3\log_{3}x&≦&4 ・・・③’
\end{eqnarray}\)
ここで
\(\,X=\log_{3}x\,,\,Y=\log_{3}y\,\)
とすると、
\(\,②’\,\)は
\(\begin{eqnarray}\displaystyle
X+\frac{1}{2}Y&≦&5\\
\fbox{ 2 }X+Y&≦&\fbox{ 10 } ・・・④
\end{eqnarray}\)
\(\,③’\,\)は
\(\begin{eqnarray}
Y-3X&≦&4\\
\fbox{ 3 }X-Y&≧&\fbox{ -4 } ・・・⑤
\end{eqnarray}\)
ヌ \(\,\underline{ 2 }\,\) ネノ \(\,\underline{ 10 }\,\) ハ \(\,\underline{ 3 }\,\) ヒフ \(\,\underline{ -4 }\,\)
ここまでは普通に条件をそろえただけです。
後はこの連立不等式を\(\,X,Y\,\)について解きます。
④⑤を\(\,X-Y\,\)座標でグラフにして表すと下のようになります。
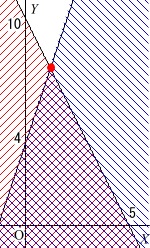 実数全体で考えると赤い点(\(\,\color{red}{●}\,\))が\(\,Y\,\)の最大値となりますが、
実数全体で考えると赤い点(\(\,\color{red}{●}\,\))が\(\,Y\,\)の最大値となりますが、
整数で最大の値を探します。
交点の座標は
\( \begin{cases}
\hspace{7pt} 2X+Y=10\\ \\
\hspace{7pt} 3X-Y=-4
\end{cases}\)
を解いて、
\(\hspace{10pt}\displaystyle \left(\,\frac{6}{5}\,,\,\frac{38}{5}\,\right)\)
つまり、
\(\hspace{10pt}\displaystyle \,Y≦\frac{38}{5}=7.6\,\)
を満たす最大の整数ということなので、
\(\,Y\,\)のとり得る最大の整数の値は\(\,\fbox{ 7 }\,\)
次に\(\,\log_{3}=Y=7\,\)としたときの②③を同時に満たす\(\,X\,\)ですが、
\(\,Y\,\)が定数になっているので、
\(\begin{cases}
\hspace{7pt} 2X+7≦10\\ \\
\hspace{7pt} 3X-7≧-4
\end{cases}\)
から
\(\hspace{10pt}\displaystyle X\,≦\,\frac{3}{2}\) かつ\(\hspace{10pt} X\,≧\,1\)
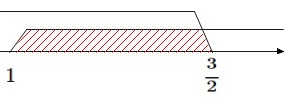 よって、
よって、
\(\hspace{10pt}\displaystyle 1\,≦\,X\,≦\,\frac{3}{2}\)
\(\,X=\log_{3}x\,\)にもどすと底が\(\,1\,\)より大きいので真数の大小が一致します。
\(\begin{eqnarray}
1≦&\log_{3}x&≦\frac{3}{2}\\
\log_{3}3^1≦&\log_{3}x&≦\log_{3}3^{\frac{3}{2}}\\
3^1≦&x&≦3^{\frac{3}{2}} ・・・⑥\\
3≦&x&≦3\sqrt{3}=5.・・・
\end{eqnarray}\)
このことから\(\,x\,\)のとり得る最大の整数は\(\,\fbox{ 5 }\,\)となります。
\(\,\sqrt{3}=1.732\cdots\,\)という値を覚えていない場合、
正の数の大小は\(\,2\,\)乗しても変わらないので
\(\begin{eqnarray}
3^1≦&x&≦3^{\frac{3}{2}}\\
3^2≦&x^2&≦3^3\\
9≦&x^2&≦27
\end{eqnarray}\)
これを満たす整数\(\,x\,\)は\(\,4\,\)か\(\,5\,\)なので、(\(\,3\,\)もでした。笑)
最大値は\(\,\fbox{ 5 }\,\)としても良いです。
第\(\,1\,\)問は以上です。
三角関数の加法定理と合成、指数対数の基本定理(公式)を使えるか確認できる問題でした。
⇒ 2020年度センター試験数学2B第2問(微分積分)の解説
第\(\,2\,\)問は接線と面積、微分積分です。
文字がいくつか出てくるのでややこしいですが、やることは同じです。
問題構成が定着してきた頃に共通テストに変わり、変化があるのでしょうか。
変化があっとしても数学は変わりませんから、焦らず基本の復習をしましょう。