等差数列の一般項と和を求める方法とその応用です。
数列で最初に出てくるのが等差数列ですが一般項や和の公式を覚える必要はありません。
何故かというと考え方さえ覚えれば一般項の公式や和の公式は覚えなくても求めるられるようになるからです。
等差数列の基本問題と最大値問題へのグラフ利用を具体的にみてみましょう。
数列の勉強法
数列は、「規則性」を持った数の集まりです。
だから大切なことは公式を覚えることではなく、書き出して規則性を見つけることなのですが、これをやらない人が多いので「数列は難しい」となるのです。
数学が得意な人の中には
「公式を覚える数学は数学ではない」
「数学は考えることで克服しろ」
という人もいます。
ですが筆者は「公式を覚えて使うでいい」と思いっきりお勧めしています。笑
(便利なものがあるなら使えばいい、ということです。)
では何故この数列だけは公式を覚えることを勧めないのか?
勧めないのではありません。
公式を覚えることができるなら覚えて使って構いませんし、その方がはやいこともあります。
いや、覚えて使えるくらいやりこんで欲しいとさえ思う単元です。
ただ、高校で数列を習うと、
公式にたよった計算分野だと思ってしまう人が多いからです。
公式を忘れたら解けないし、間違えて覚えると余計ややこしい単元でもあります。
だから、小学生でもできると思える等差数列だけでも、パズル感覚で数列に取り組んでみませんか?
ということなのです。
難しくはありません。
共通テスト(センター試験)では計算力のみを問うているような複雑な計算が待っていますので、
計算力、というより文字式を処理する力は高めておく必要がありますがここでは例題の中で基本の点検をすることとしましょう。
等差数列の例題と解答手順の基本
解答の手順を例題で見ていきましょう。
次の問いに答えよ。
(1)第3項が\(\,17\,\),第9項が\(\,38\,\)である等差数列の第15項を求めよ。
(2)初項が\(\,100\,\),公差が\(\,-4\,\)の等差数列の初項から第 \(n\) 項までの和の最大値を求めよ。
等差数列の一般項を求める基本手順
問題に「等差数列」と見たら、『初項』と『公差』、は真っ先に求めて下さい。
ほとんどの問題で誘導されますが、何も聞かれなくても関係なく求めて下さい。
初項を\(\,a\,\) , 公差を\(\,d\,\)とおくと、
等差数列は、
\( a\,,\,a+d\,,\,a+2d\,,\,a+3d\,,\,a+4d\,,\cdots,\)
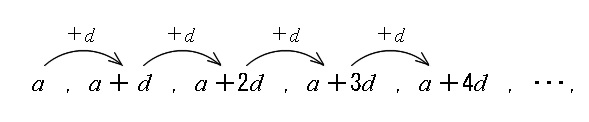
(等差数列の問題ではこの文字列を書き出せばほぼ終了します。)
と続きます。
第\(\,n\,\)項までには、公差\(\,d\,\)は\(\,(\,n-1\,)\,\) 回、初項\(\,a\,\)に足されることになるので、
一般項\(\, a_n\,\)は、
\(\hspace{10pt}\color{red}{a_n=a+(n-1)\,d}\)
となるのですが、この公式は既に覚えているでしょう。
しかし、上の規則性から出てきた公式であることを忘れないで下さい。
1分だけ時間を惜しまず上の文字列(実際には数字の列)を書き出すなら公式は必要ありません。
では問題を解いて行きましょう。
「等差数列」なので初項と公差は求めておきましょう。
(1)第3項が\(\,17\,\),第9項が\(\,38\,\)である等差数列の第15項を求めよ。
(1)「第3項が\(\,17\,\),第9項が\(\,38\,\)」より、
初項を \( a\) ,公差を \( d\) として
\(a_3=a+2d=17\) ・・・①
\(a_9=a+8d=38\) ・・・②
①,②より、\( a=10 , \displaystyle d=\frac {7}{2}\) ・・・③
③より第\(\,15\,\)項は、
\(\begin{eqnarray} \displaystyle
a_{15}&=&a+14d\\
&=&10+14 \times \frac {7}{2}\\
&=&59
\end{eqnarray}\)
条件が2つあれば必ず初項と公差はでますので、
①,②を連立しておくことがポイントですね。
この問題に限っていえば、②-①より \( \color{red}{6d =21}\) が出てきます。
\(a_9=\color{blue}{a+8d=38}\) とわかっているので
\(\begin{eqnarray}
a_{15}&=&a+14d \\
&=& \color{blue}{a+8d} +\color{red}{6d} \\
&=&\color{blue}{38}+\color{red}{21}\\
&=&59\end{eqnarray}\)
と初項、公差を求めなくても出せるのですが、基本通り「初項」「公差」は求めておくようにすると良いですね。
その問題だけに使えるのでなく、すべてに使える方法を先に覚えて下さい。
基本をしっかり抑えていけば工夫する余裕は後ででてくるようになります。
等差数列の和の求め方
(2)「初項が\(\,100\,\),公差が\(\,-4\,\)の等差数列の初項から第\(\,n\,\)項までの和の最大値」
「等差数列の和の最大値」です。
公差が正の数なら増えるだけなので最大値はありませんが、公差が\(\,-4\,\)なのでどこかで負の数が出てきます。
負の数は加えると和は小さくなるので、正の数(または0)までの和が最大ということになります。
\(100\,+\,96\,+\,\cdots \,+\,4\,+\,0\,\color{red}{-\,4\,-\,8\,-\,\cdots}\)
赤文字部分は加えると和が小さくなる。
だから、
\(\hspace{10pt}100+96+\cdots+4\)
または
\(\hspace{10pt}100+96+92+\cdots+4+0\)
までの和が最大です。
このように書き出せば、答えの最大値は簡単に出せます。
等差数列の和の公式は覚えていると思いますが、上の和を具体的に計算して、その後公式化してみます。
\(100+96+92+・・・・+4\)
の最後の\(\,4\,\)は等差数列の一般項
\(\hspace{10pt} a_n=100-4(n-1)=4\\ \\
\hspace{5pt} \Leftrightarrow \hspace{5pt}4(n-1)=100-4\\ \\
\hspace{5pt} \Leftrightarrow \hspace{5pt}4(n-1)=96\\ \\
\hspace{5pt} \Leftrightarrow \hspace{5pt}n-1=24\\ \\
\hspace{5pt} \Leftrightarrow \hspace{5pt}n=25\)
から第\(\,25\,\)項です。
\(100+96+\cdots+4\) の和は、
「初項と末項」、「第2項と末項の前の項」、・・・
と加えるとそれぞれの和は\(\,104\,\)となります。
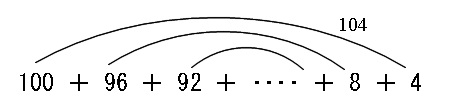
(片方は4減って、もう片方は4増える)
この組がいくつあるかというと項数の半分です。
(2つの項をセットにするから)
よってこの和は、
\( \displaystyle (100+4) \times \frac{25}{2}=1300\)
(第\(\,25\,\)項までの和)
同様に、\(100+96+92+\cdots+4+0\) を計算すると
「それぞれの和\(\,100\,\)」が「\(\,26\,\)項の半分の組数」あるので
\( \displaystyle (100+0) \times \frac{26}{2}=1300\)
(第\(\,26\,\)項までの和)
と算数で答えが出せますね。
等差数列の和の公式
では、等差数列の和の公式を使って求めてみましょう。
初項 \( a\) ,公差 \( d\) の等差数列の第 \( n\) 項までの和を \( S_n\) とすると、

先程と同様に、
初項と末項の和 \( \color{red}{a+a+(n-1)d}\) が「項数の半分の組数」あるので
\(\begin{eqnarray}\displaystyle
S_n&=&a+(a+d)+\cdots+\{a+(n-1)d\}\\
&=&\color{red}{\frac{n}{2}\times \{2a+(n-1)d\}}\end{eqnarray}\)
これが公式と知られる等差数列の和です。
数列のグラフ利用
この問題では初項\(\,100\,\),公差\(\,-4\,\)なので、
第 \(n\) 項までの和 \( S_n\) は、
\(\begin{eqnarray} \displaystyle
S_n&=&\frac{n}{2}\,\{\,200-4(\,n-1)\}\\
&=&-2\,n^2+102\,n
\end{eqnarray}\)
となります。
これは2次関数で上に凸なグラフを示します。
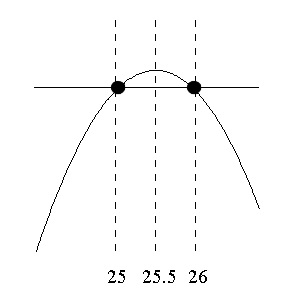
ただし、数列において \(n\) は整数しかとらないので、
飛び飛びの値で、頂点が最大とは限りません。
ここが注意点です。
平方完成すると、
\(\begin{eqnarray} \displaystyle
S_n&=&-2( n^2-51n )\\
&=&-2\left(n-\frac{51}{2}\right)^2+\frac{51^2}{2}
\end{eqnarray}\)
軸となる\(\displaystyle \,\frac{51}{2}=25.5\,\)なので、
\(\,n=25\, か\, 26\,\) で頂点(軸)に近い方が最大値となりますが、
\( n=25\,,\,26\) ともに \(S_n\) の値は同じです。
よって、
\(\,n=25\,\) または \(\,26\,\) のとき和は最大で\(\,\underline{ 1300 }\,\)となります。
数列でもグラフを利用します。
ただし、\(n\) は整数(自然数)の値しかとらないので、値が連続ではないということは忘れないで下さい。
頂点が最大とは限らず、軸に近い方が最大となりますし、
今回のように同じ値をとる2つの \(n\) が存在する場合もありますね。
共通テスト(センター試験)では数列と微分の融合というのは考えにくいですが、
2次関数はどこの分野にも出没するし、
増減表など、1つひとつの項目をしっかり定着させておくと良いですね。
等比数列の基本もしっかり確認して、融合されても対応できる、本試験でも活かせるようにしておきたいものです。
この単元が終われば全体を見渡せるようになります。
情報量が割と多めの単元なので少し時間を取って取り組むと良いですね。