このページでは部分分数などの計算問題でちょっと工夫が必要なシグマ(Σ)の計算問題を取り上げて説明します。
シグマの計算方法、表し方など今までいろいろと説明してきました。
シグマの扱いには慣れてきたと思うのでここまで来れば後はシグマを使い倒すのみです。
ここまでついてきてくれた人はきっとΣ計算は大丈夫です。
いよいよ工夫が必要なパターンに入ってきました。
テクニックと言えるかどうかは分かりませんが、知っているかいないかで差が出ますので覚えておいた方が良いでしょう。
少し工夫が必要な和の計算
分数の和の求め方と無理数を含んだ分数の和の計算です。
部分分数
「 \(\displaystyle S=\frac{1}{1\cdot3}+\frac{1}{3\cdot5}+\frac{1}{5\cdot7}+\cdots+\frac{1}{(2n-1)(2n+1)}\) を求めよ。」
「シグマの表し方」でも説明しましたが、問題で因数が2つに分けて書いてあるときは因数を前と後ろで別々に見ると良いですよ。
分母にあっても同じで、これは典型的な「部分分数」のパターンです。
\( \displaystyle \frac{1}{1\cdot3}+\frac{1}{3\cdot5}+\frac{1}{5\cdot7}+\cdots+\frac{1}{(2n-1)(2n+1)}\)
分母の因数2つの、
前は 1,3,5,・・・ で、1から始まる奇数 \(2n-1\)
後は 3,5,7,・・・ で、3から始まる奇数 \(2n+1\)
となっています。
\( k\) 番目の項を見ると、
\( \displaystyle \frac{1}{(2k-1)(2k+1)}\)
ですが、これを
\( \displaystyle \frac{1}{(2k-1)}-\frac{1}{(2k+1)}\)
と分数の差として分けます。
単純に分けられるのではなく、
\( \displaystyle \frac{1}{(2k-1)(2k+1)}\)
と等しくするために、
\( \displaystyle \frac{1}{(2k-1)(2k+1)}=\color{red}{\frac{1}{2}}\left\{\frac{1}{(2k-1)}-\frac{1}{(2k+1)}\right\}\)
としなければなりません。
この \(\displaystyle\frac{1}{2}\) は \(\displaystyle \frac{1}{(2k-1)}-\frac{1}{(2k+1)}\) を通分することで見つけることができます(※①)。
通分すると
\( \displaystyle \frac{1}{(2k-1)}-\frac{1}{(2k+1)}=\frac{(2k+1)-(2k-1)}{(2k-1)(2k+1)}=\frac{2}{(2k-1)(2k+1)}\)
となることから逆に、
\( \displaystyle \frac{1}{(2k-1)(2k+1)}\\ \\
=\displaystyle \frac{1}{2}\times \displaystyle \frac{2}{(2k-1)(2k+1)}\\ \\
=\displaystyle \frac{1}{2}\left(\displaystyle \frac{1}{2k-1}-\displaystyle \frac{1}{2k+1}\right)\)
とできるのです。
決まっている数値ではありませんので、実際にそのときそのときに通分して見つけて下さい。
※①
実は、\( 2k-1\) と \( 2k+1\) の差が 2 なので分母に2を持ってくれば良いのですが、因数が3つなどになると違った方法になりますので、覚えておくより通分してその都度求めた方が確実です。
では、部分分数に変形できたとして計算をしてみましょう。
これは公式などは使えません。
そもそも分数にΣ計算の公式は使えませんからね。
Σの基本である「和を具体的に書き出す」ことをすればすぐに解決します。
\( \displaystyle S=\frac{1}{1\cdot3}+\frac{1}{3\cdot5}+\frac{1}{5\cdot7}+\cdots+\frac{1}{(2n-1)(2n+1)}\\ \\
\displaystyle =\sum_{k=1}^n\frac{1}{(2k-1)(2k+1)}\\ \\
\displaystyle =\sum_{k=1}^n\frac{1}{2}\left\{\frac{1}{(2k-1)}-\frac{1}{2k+1)}\right\}\\ \\
\displaystyle =\frac{1}{2}\left\{\left(\frac{1}{1}-\frac{1}{3}\right)+\left(\frac{1}{3}-\frac{1}{5}\right)+\left(\frac{1}{5}-\frac{1}{7}\right)+\cdots+\left(\frac{1}{2n-1}-\frac{1}{2n+1}\right)\right\}\)
ここで前後で消し合うので
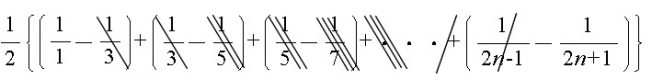
残るのは、最初と最後の項となります。
\( \displaystyle S=\frac{1}{2}\left(\frac{1}{1}-\frac{1}{2n+1}\right)\\ \\
\displaystyle ~\hspace{10pt}=\frac{1}{2}\times \frac{(2n+1)-1}{2n+1}\\ \\
\displaystyle ~\hspace{10pt}=\frac{n}{2n+1}\)
なんだか長くなってややこしそうに見えるけど、やってることは簡単なことなので少し練習して見て下さい。
すぐに使えるようになりますから。
打ち消し合う部分を見極めるには、
「できるだけ多く具体的に書き出す」
ことです。
無理数を含んだ分数の和
「 \(\displaystyle S=\frac{1}{\sqrt{1}+\sqrt{2}}+\frac{1}{\sqrt{2}+\sqrt{3}}+\frac{1}{\sqrt{3}+\sqrt{4}}+\cdots+\frac{1}{\sqrt{n}+\sqrt{n+1}}\) を計算せよ。」
(この問題まではクリアーできると良いですね。)
これも練習28と同じで、ちょっとした変形(有理化)で順次消し合って残るのが一部分だけ、という形になるんです。
項の一つひとつを有利化しても良いのですが、いくつも有理化するのは時間がかかります。
全体をΣで表したあと \(k\) の式を有理化しておけば一度で済みます。
これを利用すれば、
\( \displaystyle S=\sum_{k=1}^n {\frac{1}{\sqrt{k}+\sqrt{k+1}}}\\ \\
\displaystyle =-\sum_{k=1}^n {(\sqrt{k}-\sqrt{k+1}})\\ \\
\displaystyle =-\{(\sqrt{1}-\sqrt{2})+(\sqrt{2}-\sqrt{3})+(\sqrt{3}-\sqrt{4})+\cdots+(\sqrt{n}-\sqrt{n+1})\}\\ \\
\displaystyle =-(\sqrt{1}-\sqrt{n+1})\\ \\
\displaystyle =\sqrt{n+1}-1\)
と計算せずに終わります。
有理化したとき、
\( \displaystyle \frac{1}{\sqrt{k}+\sqrt{k+1}}=\sqrt{k+1}-\sqrt{k}\)
とすることもできますが、打ち消しを見るときに飛び飛びになり、
\(\displaystyle S=(\color{red}{\sqrt{2}}-\sqrt{1})+(\color{magenta}{\sqrt{3}}-\color{red}{\sqrt{2}})+(\sqrt{4}-\color{magenta}{\sqrt{3}})+\cdots+(\sqrt{n}-\sqrt{n+1})\)
消えるところ、残るところがわかりにくいですよね。
分かりづらいので「-」でくくり
\( \displaystyle S=-\sum_{k=1}^n (\sqrt{k}-\sqrt{k+1})\)
の形にしましたが、どちらでも構いません。
しかし試験中には気がつかないこともありますよね。
そういう場合は、書き出す項を多くすると分かりやすくなる,というより多く書き出すべきです。
\( S=(\sqrt{2}-\sqrt{1})\\~\hspace{10pt}+(\sqrt{3}-\sqrt{2})\\~\hspace{10pt}+(\sqrt{4}-\sqrt{3})\\~\hspace{10pt}+(\sqrt{5}-\sqrt{4})\\~\hspace{10pt}+(\sqrt{6}-\sqrt{5})\\~\hspace{10pt}+\cdots \\~\hspace{10pt}+(\sqrt{n-2}-\sqrt{n-3})\\~\hspace{10pt}+(\sqrt{n-1}-\sqrt{n-2})\\~\hspace{10pt}+(\sqrt{n}-\sqrt{n-1})\\~\hspace{10pt}+(\sqrt{n+1}-\sqrt{n})\)
で消していけば、何が残るか、少しは見えてきますか?
場合分けを考える和にシグマを使う場合
「 \(S=1^2-2^2+3^2-4^2+\cdots+(2n-1)^2-(2n)^2\) を計算せよ。」
(この問題からは余裕ができてから見て下さい。)
平方数の和と差が繰り返されますが、項は偶数個あります。
それで2つずつ見ていくとうまくいくわけですが、偶数項で終わっていなければこの方法はとれません。
項数が奇数のときと偶数のときで違ってくるのです。
\( S=1^2-2^2+3^2-4^2+\cdots+(2n-1)^2-(2n)^2\)
\( S=1^2-2^2+3^2-4^2+\cdots+(2n-1)^2\)
これを問題として取り上げたのは、
たとえば、
\( S=1-1+1-1+1-+\cdots+(-1)^{n-1}\)
は、
\(n\) が奇数のとき \( S=1\)
\(n\) が偶数のとき \( S=0\)
となり答えが違ってくるので場合分けが必要で、数学Ⅲではこのような問題が多くなってくるので取り上げておきました。
(この問題は数学Ⅲで無くてもでます。)
練習30は偶数項の場合だけを考えれば良いので、計算練習だと思って見ておいて下さい。
\( \displaystyle S=1^2-2^2+3^2-4^2+\cdots+(2n-1)^2-(2n)^2\\ \\
\displaystyle =(1^2-2^2)+(3^2-4^2)+\cdots+\{2n-1)^2-(2n)^2\}\\ \\
\displaystyle =\sum_{k=1}^n \{(2k-1)^2-(2k)^2\}\\ \\
\displaystyle =\sum_{k=1}^n \{(4k^2-4k+1)-(4k^2)\}\\ \\
\displaystyle =\sum_{k=1}^n (-4k+1)\\ \\
\displaystyle =-4\sum_{k=1}^n k+\sum_{k=1}^n 1\\ \\
\displaystyle =-4\cdot \frac{1}{2}n(n+1)+n\\ \\
\displaystyle =-2n(n+1)+n\\ \\
\displaystyle =n(-2n-2+1)\\ \\
\displaystyle =n(-2n-1)\\ \\
\displaystyle =-n(2n+1)\)
もしも奇数項までの和だったら、
最後の項の1つ手前までなら偶数項なので最後の項だけ別に加えれば
\( \displaystyle S=\sum_{k=1}^{n-1}\{(2k-1)^2-(2k)^2\}+(2n-1)^2\\ \\
~\hspace{10pt}=n(2n-1)\)
となりますね。
練習31以降の問題は明らかにセンター試験レベルを超えていますので、
別に応用編として記事にしますのでシグマ(Σ)計算としてはここで終了とします。
ここまででも読んでいる人は少ないと思いますが、笑
逆にここまでが自分でできるようになればセンター試験の数列の計算レベルには達しています。
後は「階差数列」や「漸化式」「数学的帰納法」といった用語を理解するかどうかでしょう。
シグマは「和」です。
計算公式を含めた使い方をしっかり身につけて数列を克服してくださいね。
シグマに不安があるときは
から復習してください。
漸化式をマスターしたいなら
⇒ 漸化式の解き方パターン一覧と一般項の求め方まとめ(階差数列、分数、累乗など)
にチャレンジして下さい。
解けない漸化式はなくなります。