高次式とは整式の中でも次数の高いもの(といっても3次式が多い)を示します。
整式の割り算のやり方はやって見れば簡単ですので、見るだけではなく実際にやって見てください。
ここでは少し楽できる方法も紹介しておきます。
式の値を求めるときに役に立ちますので割り算の仕方は覚えておいた方が良いですよ。
高次式が問題に出てくるときにやるべきこと(問題が問うていること)は大きく2つあります。
もちろんそれだけではありませんが、この2つは必ず意識しておきましょう。
高次の整式を扱う問題のポイント2つ
1つは整式の割り算ができるか、実際に割り算しているかということです。
これは整式の項目では「できなくてはならないこと」としてよく問題にされます。
もう一つは、
整式の値を求めるとき、「割り算が利用出来ていますか」、ということです。
例題を見ながら進めた方が分かりやすいですね。
\(x=2-\sqrt{3}\) のとき \( x^3-7x^2+15x-3\) の値を求めよ。
この問題を見て、代入することを考えたなら飛ばして次の問題に行った方が良いです。
時間がかかる上にミスしやすいので他の問題で点を取りに行った方がマシです。
あちこちで書いていますが、
このような条件式を見たらやることはほぼ決まっています。
無理数部分を残して移項し、両辺を平方するのです。
\( x=2-\sqrt{3}\) 移項して \( x-2=-\sqrt{3}\)
両辺平方します。
\( (x-2)^2=(-\sqrt{3})^2\)
これは逆は成り立ちませんが条件式からは成り立つので、必要条件、十分条件は気にせず使って構いません。
この2次式は
\( (x-2)^2=(-\sqrt{3})^2\\ \\
\Leftrightarrow \hspace{10pt} x^2-4x+4=3\\ \\
\Leftrightarrow \hspace{10pt} x^2-4x+1=0 ・・・①\)
まで変形しておくと使いやすいことが多いです。
ここまでは問題によらず条件式を見た瞬間にやってもらいたいくらいです。
間違っても \( x=2-\sqrt{3}\) を与式に代入して計算するなんて算数はやめてください。
①ですが使い方が2つあります。
先ずは割り算とは関係ない使い方を紹介します。
高次式の次数を下げる方法
\( x^2-4x+1=0\) を \( x^2=4x-1\) として与式を変形すると
\( x^3-7x^2+15x-3\\ \\
=(x^2)x-7(x^2)+15x-3\\ \\
=(4x-1)x-7(4x-1)+15x-3\\ \\
=4x^2-x-28x+7+15x-3\\ \\
=4(x^2)-14x+4\\ \\
=4(4x-1)-14x+4\\ \\
=16x-4-14x+4\\ \\
=2x\\ \\
=2(2-\sqrt{3})\)
ここではたまたま定数項が0になりましたが、①を何度も利用すれば何次式であろうと必ず、
「1次以下」の整式まで次数を下げることが出来ます。
「次数下げ」と呼ばれる方法ですが1次の項が消えて定数項になることもあります。
しかし、これはまだ3次式だからこの程度で済みますが、もっと次数の高い整式だとものすごい時間がかかり計算ミスも激増します。
といっても極端に次数の高い計算はもっと別の解法が出てきますので、これはこれで使える方法です。
ただ、割算を利用する方法を知っていればこれはやっかいな解法に見えてきます。
高次の整式の割り算のやり方
整式の割り算はやって見るかどうかだけで難しいことはありません。
やって見れば簡単です。
\( x^3-7x^2+15x-3\) を \( x^2-4x+1\) で割ってみましょう。
先ずは普通の割り算みたいに、「割られる式」と「割る式」を書きます。
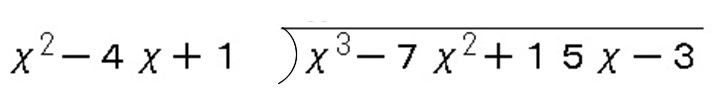
次に割られる式の1番次数が高い項を消すように、割る式とかける項を消したい項の上に書き出します。
この場合係数が1なので \( x\) です。
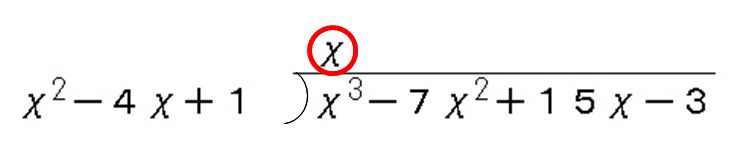
次は「上に書いた文字式と割る式をかけた式」を割られる式の下にそろえて書いていきます。
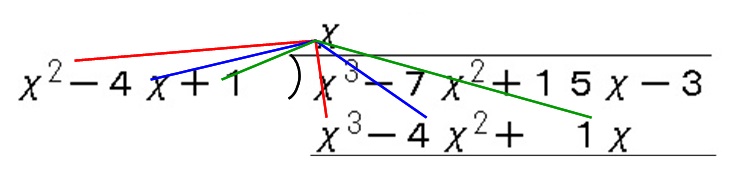
次は割られる式から今書き出した式を引きます。
引き算した結果を下に書き出します。
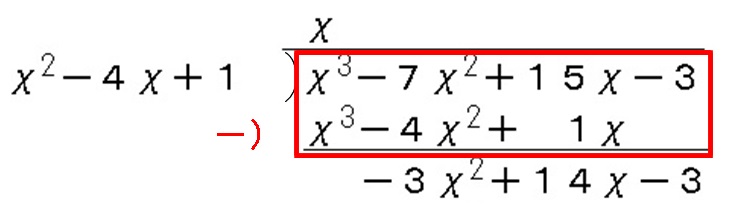
この時点で最高次数の項は消えているはずです。
今度は残りの最高次数の項を消すように割り算します。
残りの最高次数の係数が「-3」なので-3を上に書きます。
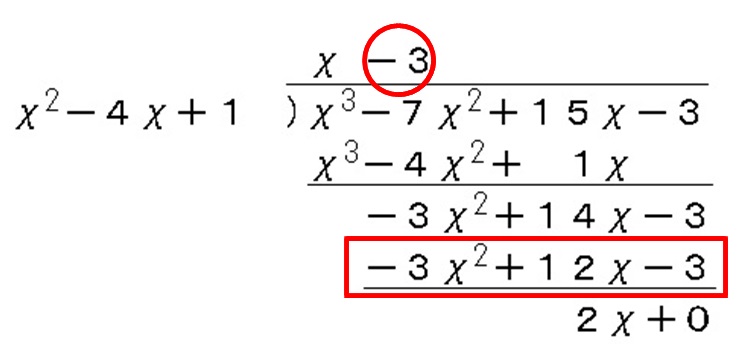
先程と同じように割る式と「-3」をかけて残りの式の下に書き出し、
引き算をすれば割り算の完成です。
2次式で割っているのであまりが2次以上になることはありません。
余りは1次以下、つまり一次式か定数、となります。
割り算はできるようになっているということで先に行きます。
割り算したところで何が言えるのか?
\( x^3-7x^2+15x-3\) を \( x^2-4x+1\)で割ると
商が \( \color{red}{x-3}\) 余りが \(\color{green}{2x}\) であったということは、
\( x^3-7x^2+15x-3=(x^2-4x+1)(\color{red}{x-3})+\color{green}{2x}\)
という関係式が成り立つということです。(割り算の定義)
ここで \( x^2-4x+1=0\) なので
\((x^2-4x+1)(x-3)=0\) となり、
\((与式)=2x\\ \\
=2(2-\sqrt{3})\)
と答えが求まります。
説明は長いですが割り算できるならはやいです。
これは(与式)が高次の整式の場合でも使えるので「次数下げ」よりはかなり速く処理できます。
是非とも習得しておいて下さい。
それとこの割り算ですが、
係数だけを書いて計算すると時間短縮できます。
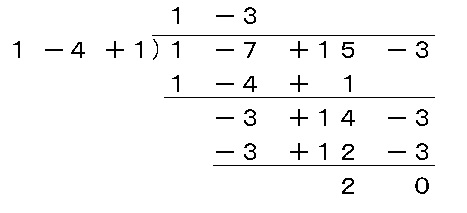
2、3回練習するだけでも普通にできるようになるのでやって見てください。
やって見ないと時間かかるように思えてしまい、後々時間がもったいないですよ。
注意するとすれば、3次式で2次の項がないなど次数がとんだ場合、
例えば、\( x^3+15x-3\) などのときは、\(x^2\) の項が係数0であるとして、間を空けるか、0を書いておくことです。

のようにです。
しつこいですが、ものすごく高次式で無い限り、何次式でもこの割算を利用した式変形をすれば、次数下げと違ってかかる時間はほぼ同じとなります。
3次式、4次式の求値問題ではほぼ変わりませんので使って下さい。
記述式の解答をするときの注意点
条件式から \( x^2-4x+1=0\) はわかっているのですが、
与式を変形するとき、
「与式を \(x^2-4x+1=0\) で割ると」
と書くのは絶対ダメです。
そもそも方程式で割るということが意味がわからないし、0で割るということはできませんので、割り算は別のところでしたことにして、
(解答横に割り算を書いておくのは別にかまいません。)
「与式は
\( x^3-7x^2+15x-3=(x^2-4x+1)(x-3)+2x\)
と変形でき、\(x^2-4x+1=0\) なので、、、」
と書いておけば大丈夫ですよ。
\( x^{2020}\) の値、なんて問題もでくくるでしょうが、別の解法になるので機会があればまた紹介します。
条件式の変形は大きなポイントになるので
といった基本的な復習もやっておきましょう。
⇒ 式と証明の要点
二項定理や恒等式を含む式の証明単元のまとめです。
高次方程式を解くときにも整式の割り算は使いますよ。