判別式は判定式とも呼ばれ、2次方程式を扱うときの重要な役割をしています。
使い方はいろいろありますが、実数解の個数を求めることや、実数解の個数による係数の範囲を求める問題に利用出来ます。
2次関数と2次方程式は共有点問題で共通する部分が多いので判別式は使える範囲がかなり広いです。
判別式
\( ax^2+bx+c=0( a \neq 0 )\)
において \( b^2-4ac\) を判別式といって \( D\) と書きます。
判別式 : \(\large{ \color{red}{D=b^2-4ac}}\)
です。
2次方程式の解の公式はこの判別式を用いて表すと、
\( x=\displaystyle \frac{-b \pm \sqrt{b^2-4ac}}{2a}\\ \\
=\displaystyle \frac{-b \pm \sqrt{D}}{2a}\)
となります。
2次方程式の解の判別
\( a,b,c\) を係数に持つ2次方程式では解の公式は
\( x=\displaystyle \frac{-b \pm \sqrt{D}}{2a}\)
なので、\( ax^2+bx+c=0\) の解について
① \( \color{red}{D>0}\) のとき、異なる2つの実数解を持つ。
(2つの実数解を持ち、その2つの実数解は異なるということです。)
② \(\color{red}{ D=0}\) のとき、重解を持つ。
(2つの実数解は一致して、見かけ上1つの実数解をもつということです。)
③ \( \color{red}{D < 0}\) のとき、実数解は待たず、2つの虚数解をもつ。
(実数解だけでいえば、実数解は持たない「解なし」ということです。)
このように解の個数が判別されます。
これらは判別式 \( D\) が解の公式のルートの中の式であることからすぐにわかります。
判別式を利用する例題
\(x^2-4x+k=0\) の解を判別せよ。
\( x^2\) の係数が1なので2次方程式ということは分かっています。
(係数が0の可能性も文字の場合には考えなくてはなりません。)
判別式は
\( D=(-4)^2-4\cdot 1 \cdot k\\ \\
=4(4-k)\)
\( D\) の符号により
ⅰ) \(D>0 \Leftrightarrow k < 4\) のとき、異なる2つの実数解を持つ。
※
\( D>0\) のときであり、
\( 4(4-k)>0\\ \\
\Leftrightarrow \hspace{10pt} 4-k>0\\ \\
\Leftrightarrow \hspace{10pt} k < 4\)
符号ミスを減らすためにもここの符号は慎重に確認しましょう。
ⅱ) \( D=0 \Leftrightarrow k=4\) のとき、実数の重解を持つ。
ⅲ) \( D<0 \Leftrightarrow k>4\) のとき、実数解を持たない。(2つの虚数解)
と判別出来ます。
「実数解の個数を調べよ。」
という問題のときは虚数解については触れなくても良いですよ。
ここでは複素数を知っている人に向けて補足として書いています。
判別式と2次関数のグラフ
2次関数 \(y=ax^2+bx+c\) のグラフと,
\(x\) 軸との共有点の \(x\) 座標は、
\( y=ax^2+bx+c\) において \( y=0\)( \( x\) 軸の方程式 )として得られる2次方程式
\( ax^2+bx+c=0\)
の実数解です。
このことと判別式の意味を合わせると
\( ax^2+bx+c=0\) の判別式を \( D\) とすると2次関数は、
\( D>0\) のとき \( x\) 軸と2点で交わっています。
( \( a\) が正のときは下に凸、負のときは上に凸)
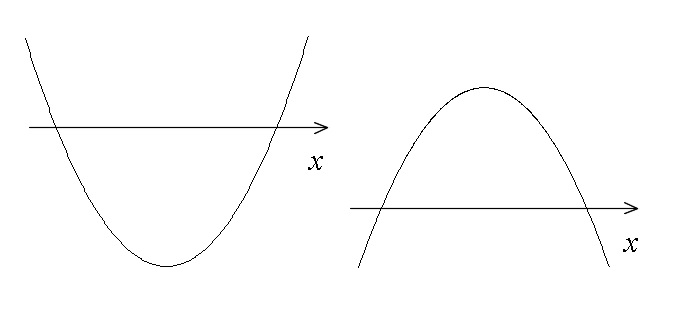
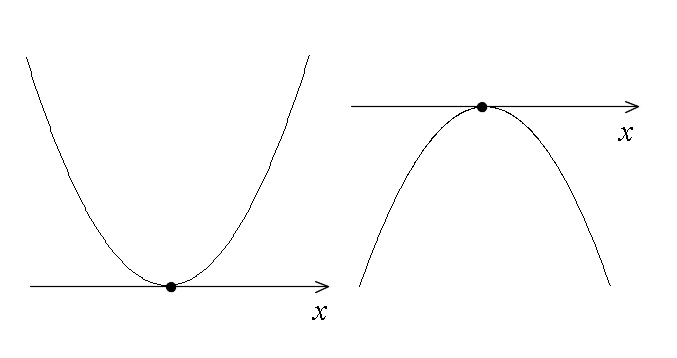
\(D=0\) のとき \( x\) 軸と1点で交わって(接して)います。
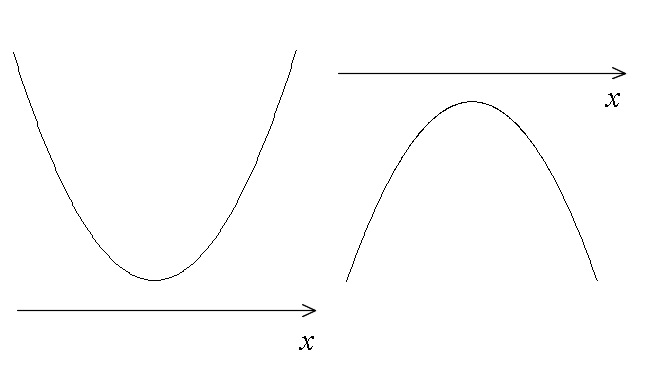
\( D < 0\) のとき \( x\) 軸とは離れていて共有点はありません。
グラフに関してまとめます。
\( ax^2+bx+c=0\) の判別式を \( D\) とすると
2次関数 \( y=ax^2+bx+c\) のグラフと \( x\) 軸は、
① \( \color{red}{D>0 のとき2点で交わる。}\)
② \(\color{red}{ D=0 のとき1点で接する。}\)
③ \(\color{red}{ D <0 のとき共有点を持たない。}\)
ということです。
判別式は2次不等式などにも利用出来ます。
2次関数、2次方程式などの主要部分なので必ず使えるようにしておきましょう。
判別式は解の公式のルートの中身です。
判別式のもう一つの形
判別式は2次方程式 \( ax^2+bx+c=0\) における \( b^2-4ac\) のことです。
この方程式の解を \( \alpha, \beta\) とすると
\( \color{red}{D=a^2(\alpha-\beta)^2}\)
という形でも表せますが、この式の説明はおいておきます。
ここでは良く使う形を1つ確認しておきます。
2次方程式が \( ax^2+2b’x+c=0\) となっている場合、
\(\color{red}{x の係数が偶数の場合}\) ですね。
このときの判別式はもっと簡単な形のもので表せます。
普通に判別式を計算すると
\( D=(2b’)^2-4\cdot a\cdot c\\ \\
=4b’^2-4ac\\ \\
=4(b’^2-ac)\)
符号を考えるとしてもこの式は
\( \color{red}{D/4=b’^2-ac と同値}\) です。
なので \( x\) の係数が偶数のときは
\( D’=D/4=b’^2-ac\) を判別式に使うことができます。
もちろん \( D\) のまま計算しても結果は同じなのですが、
問題によっては計算量がかなり違って来ます。
「 \( D\) で計算できるから覚えなくていいや」
ではなくて、一度覚えたらその後はずっと楽な計算で処理できるんだから、少し時間を使っても覚えておくと良いですよ。
こういうところをさぼる人は「試験時間が足りない」とかいってます。
試験時間が足りないのではなく、数学の良さを利用してないだけですからね。
試験時間が足りない。
計算が遅い。
と感じる人は一度でも良いから数学しているか、
数学の便利なところ利用しているか、
考えてみると良いのではないですか?
判別式が理解できたところで2次関数との関係もう一度見なおして見て下さい。
きっと理解が深まるはずです。
実数から数字の世界が広がりますので、時間を少しでも多くかけて慣れましょう。