三角比で成り立っている関数の最大値最小値問題は置換することによって2次関数を利用すれば出せるものばかりです。
ただし、値はすぐに出ますが注意点がありますので確認しておいてください。
2次関数をしっかり習得している人にとっては物足りないとは思いますが、うっかりミスが出るところなので気をつけてください。
三角比の最大値最小値問題の求め方
三角比の範囲で出される最大値、最小値問題は、
\(\,\sin x\,\)や\(\,\cos x\,\)を文字で置換(置きかえ)すれば単純な2次関数の問題になります。
三角関数ほどややこしい問題はありませんが、置換した値でなく、置換する前に戻すことを忘れないようにしましょう。
角度は\(\,x\,\)でも\(\,\theta\,\)でも同じです。
問題です。
(1)
\( 0^\circ ≦ x ≦ 180^\circ \hspace{4pt}\)のとき
関数 \( y=4\cos x(\cos x-1)\hspace{4pt}\)の最大値、最小値を求めよ。
(2)
\( 0^\circ ≦ \theta ≦ 180^\circ \hspace{4pt}\)のとき
\( 4\sin^2 \theta+4\cos \theta+3\hspace{4pt}\)の最大値、最小値を求めよ。
\(\sin\) や \( \cos\) を含むときの最大最小を聞かれたら、置換しましょう。
置換して2次関数に持ち込むというのは普通に使われる手法なので覚えておいてください。
もし、3次関数になるような問題は微分との融合です。
焦らず増減表を書いて処理すれば問題ありませんが、
微分との組み合わせはセンター試験(共通テスト)の区切りでは分野の融合が変な組み合わせになります。
本試験で気をつけておけば良いでしょう。
置換したときの要注意点は、定義域の確認です。
これは分野に関係なく、置換したとき必ずやっておくべきことですよ。
(1)
\(\hspace{10pt}y=4\cos x(\cos x-1)\)
において、
\(\cos x=t\hspace{4pt}\)とおくと\(\hspace{4pt}-1\,≦\,t\,≦\,1\)
なので、
\(\begin{eqnarray}\displaystyle
y&=&4\cos x(\cos x-1)\\
&=&4t(t-1)\\
&=&4(t^2-t)\\
&=&4 \left\{ \left(t-\displaystyle \frac{1}{2} \right)^2-\displaystyle \frac{1}{4} \right\}\\
&=&4 \left(t-\displaystyle \frac{1}{2} \right)^2-1
\end{eqnarray}\)
当然ですが\(\,-1\,≦\, t \,≦\, 1\hspace{4pt}\)におけるグラフを書きます。

グラフは図の実線部分で、
最大値は\(\hspace{4pt}t=-1\hspace{4pt}\)のとき\(\,\underline{ 8 }\,\)
このとき、
\(\hspace{10pt}\cos x=-1\hspace{4pt}\)より\(\hspace{4pt}x=\underline{ 180^\circ }\)
最小値は、\(\displaystyle t=\frac{1}{2}\) のとき\(\,\underline{ -1 }\,\)
このとき、
\(\hspace{10pt}\displaystyle \cos x=\frac{1}{2}\hspace{4pt}\)より\(\hspace{4pt}x=\underline{ 60^\circ }\)
このように一旦\(\,t\,\)の関数として見れば簡単ですが、
最大値、最小値を与える\(\,t\,\)だけではなく、\(\,x\,\)の値も答えに添えておきましょう。
問題によっては「そのときの\(\,x\,\)も求めよ。」となっていますが、
求められていない場合でも記述式の解答には添えておく方が良いですよ。
三角比は1つに統一することがポイント
(2)
\( 4\sin^2 \theta+4\cos \theta+3\hspace{4pt}\)は関数としておかれていませんが、
\(\hspace{10pt} y=4\sin^2 \theta+4\cos \theta+3\)
の最大値、最小値となる\(\,y\,\)を探せば良いだけです。
\(\,y\,\)は\(\,k\,\)でも何でもかまいませんよ。
縦軸を何にするかの違いだけです。
ここで(1)と同様の手順で置換しますが、
その前に全体を\(\hspace{4pt}\cos \theta\hspace{4pt}\)に統一しましょう。
\(\begin{eqnarray} y&=&4\sin^2\theta+4\cos\theta+3\\
&=&4(1-\cos^2\theta)+4\cos \theta +3\\
&=&-4\cos^2\theta +4\cos\theta+7
\end{eqnarray}\)
ここで\(\hspace{4pt}\cos\theta=t\hspace{4pt}\)とおくと
\( 0^\circ ≦ \theta ≦ 180^\circ\)
において\(\,-1\,≦\, t\,≦\,1\,\)
なので
\(\begin{eqnarray}\displaystyle
y&=&-4t^2+4t+7\\
&=&-4(t^2-t)+7\\
&=&-4\left(t-\frac{1}{2}\right)^2+8
\end{eqnarray}\)
(定義域は\(\,-1\,≦\,t\,≦\,1\,\)です。 )
グラフを書くとすぐに最大最小は分かります。
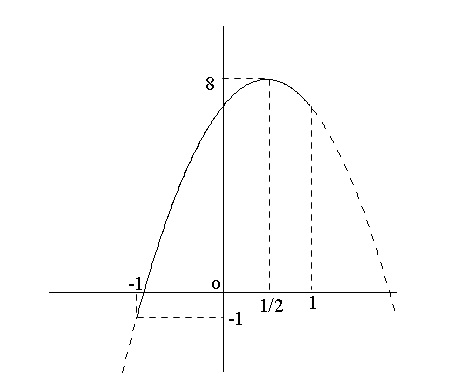
最大値は、\(\displaystyle t=\frac{1}{2}\hspace{4pt}\)のとき\(\,\underline{ 8 }\,\)
最小値は、\( t=-1\hspace{4pt}\)のとき\(\,\underline{ -1 }\,\)
となります。
よって、
\(\hspace{10pt}\displaystyle t=\frac{1}{2}\)すなわち\(\hspace{4pt}\theta=60^\circ\)のとき最大値\(\,\underline{ 8 }\,\)
\(\hspace{10pt}t=-1\)すなわち\(\hspace{4pt}\theta=180^\circ\hspace{4pt}\)のとき最小値\(\,\underline{ -1 }\,\)
2次関数の重要性の確認
途中までは三角比の問題に見えて、後半は2次関数の問題へと変わっています。
最後は置換した文字をもとに戻して\(\,x\,\)も求めますが、
2次関数の重要性は分かってもらえるでしょう。
「平方完成」 ⇒ 「グラフ」という流れですね。
三角比の方程式や最大値最小値問題では、
\(\sin\hspace{4pt}\)か\(\hspace{4pt} \cos\hspace{4pt}\)のどちらか1つで表す
ということがポイントです。
同じような例題をあげておきますので確認しておきましょう。
\(\,\theta\,\)が\(\,0^{\circ}\,≦\,\theta\,≦\,180^{\circ}\,\)の範囲のいろいろな値をとるとき、
\(\hspace{10pt}y=2\sin^2\theta+\cos\theta\)
の最大値、最小値を求めよ。
\(\hspace{10pt}\sin^2\theta=1-\cos^2\theta\,\)
を用いると、
\(\begin{eqnarray}
y&=&2\sin^2\theta+\cos\theta\\
&=&2(\,1-\cos^2\theta\,)+\cos\theta\\
&=&-2\cos^2\theta+\cos\theta+2
\end{eqnarray}\)
そこで、\(\,\cos\theta=t\,\)とおくと、
\(\begin{eqnarray}\displaystyle
y&=&-2\,t^2+t+2\\
&=&-2\left(t-\frac{1}{4}\right)^2+\frac{17}{8}
\end{eqnarray}\)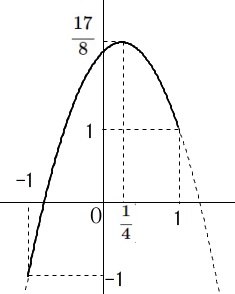 ここで
ここで
\(\hspace{10pt}0^{\circ}\,≦\,\theta\,≦\,180^{\circ}\,\)
のもとでは\(\,t\,\)のとり得る範囲は
\(\hspace{10pt}-1\,≦\,t\,≦\,1\)
グラフより
最大値 \(\displaystyle \underline{ \frac{17}{8} }\)
最小値 \(\underline{ -1 }\)
三角比の具体的な角度が求められないとき
最大値、最小値を与える\(\,t\,\)の値は平方完成された関数と定義域や、
グラフからも分かると思うので\(\,t\,\)の値から\(\,\theta\,\)も自分で求め見てください。
最小値は
\(\hspace{10pt}\,t=\cos\theta=-1\,\)
つまり\(\,\theta=180^{\circ}\,\)のときであると具体的に\(\,\theta\,\)が求まります。
しかし、最大値を与える\(\,t\,\)は具体的な\(\,\theta\,\)が分かりません。
こういう場合は、\(\,\theta\,\)を聞いてくることはありませんので答えなくて構いません。
具体的な角度が定められないときの\(\,\theta\,\)について書くとすれば、
「\(\,\theta\,\)は\(\displaystyle \,\cos\theta=\frac{1}{4}\,\)を満たす。」
と添えれば十分です。
三角比の範囲での最大値、最小値問題では具体的に求まることが多いですが、
具体的な角度が求まらないときは「ある三角比を満たす」ことを示しておけば良いです。
最大値最小値もそうでしたが、
方程式や不等式でも\( \sin\hspace{4pt}\)や\(\hspace{4pt}\cos\hspace{4pt}\)などの三角比は出てきますが、
基本になるのは方程式や2次関数の知識ですよ。
三角比に慣れたら次は応用範囲の広い図形との関係となる定理です。
これは覚えておかないと話になりませんが、簡単にクリアーできますよ。
三角関数の基礎となる三角比すべての要点を復習できます。
