三角比と図形への応用の単元「図形と計量」の要点です。
三角関数につながる基本部分ですが、図形に利用できる定理がいくつか出てきますので応用範囲は広いです。
ヘロンの公式と円に内接する四角形の面積公式までまとめておきます。
三角比と図形への応用の要点
三角比の性質はそのまま数学\(\,\mathrm{Ⅱ}\,\)の三角関数につなげることができるので、
覚えっておいた方が良い、というより覚えていないと三角関数があつかえなくなります。
また三角比は図形と深い関係がありますので図形の復習にも良い機会です。
三角比の基本
三角比であつかう角度は\(\,180°\,\)までなので、
三角形における辺の関係と考えておけば良いです。
三角比
3つの三角比を覚えておきましょう。
「三角比」という用語を使うのは三角形の\(\,3\,\)辺に関連しているからなので、
三角形を書きながら見ていくとわかりやすいです。
正弦、余弦、正接
\(\,\mathrm{∠C}\,\)を\(\,90°\,\)とする直角三角形\(\,\mathrm{ABC}\,\)において、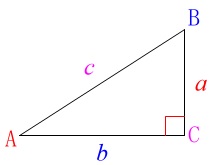
\(\hspace{10pt}\displaystyle \mathrm{\frac{BC}{AB}}=\frac{\color{red}{a}}{\color{magenta}{c}}\hspace{10pt}\)を\(\,\mathrm{∠A}\,\)の正弦(サイン)
\(\hspace{10pt}\displaystyle \mathrm{\frac{AC}{AB}}=\frac{\color{blue}{b}}{\color{magenta}{c}}\hspace{10pt}\)を\(\,\mathrm{∠A}\,\)の余弦(コサイン)
\(\hspace{10pt}\displaystyle \mathrm{\frac{AC}{BC}}=\frac{\color{blue}{b}}{\color{red}{a}}\hspace{10pt}\)を\(\,\mathrm{∠A}\,\)の正接(タンジェント)
といいます。(正接を忘れがちです。)
※
三角形の場合、
\(\,\mathrm{∠A}\,\)の対辺は\(\,a\,\)
\(\,\mathrm{∠B}\,\)の対辺は\(\,b\,\)
\(\,\mathrm{∠C}\,\)の対辺は\(\,c\,\)
と習慣的に書きますので、問題に注釈が無くても読み取って下さい。
また、正弦、余弦、正接は記号を用いて
\(\hspace{10pt}\displaystyle \sin A=\frac{\color{red}{a}}{\color{magenta}{c}}\)
\(\hspace{10pt}\displaystyle \cos A=\frac{\color{blue}{b}}{\color{magenta}{c}}\)
\(\hspace{10pt}\displaystyle \tan A=\frac{\color{red}{a}}{\color{blue}{b}}\)
と表します。
※注意
\(\,\mathrm{\sin A}\,\)を\(\,\mathrm{\sin \color{red}{∠A}}\,\)とは習慣的にしません。
今度は角の代表として用いる\(\,\color{red}{\theta}\,\)を用いて教科書的に三角比を表しておきます。
\(\color{red}{\fbox{ 三角比の定義 }}\)
直角三角形において直角を右下にして、左下の鋭角を\(\,\color{red}{\theta}\,\)とするとき、
図のように斜辺を\(\,r\,\)、対辺を\(\,\color{red}{x}\,\)、隣辺を\(\,\color{blue}{y}\,\)とすると、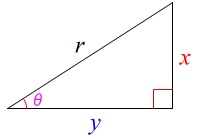
\(\begin{eqnarray}\displaystyle \sin\theta&=&\frac{\color{blue}{y}}{r}\\
\cos\theta&=&\frac{\color{red}{x}}{r}\\
\tan\theta&=&\frac{\color{blue}{y}}{\color{red}{x}}\end{eqnarray}\)
※
直角三角形において、\(\,\theta\,\)について見たとき
\(\,r\,\)を斜辺、\(\,\color{red}{x}\,\)を対辺、\(\,\color{blue}{y}\,\)を隣辺
といいます。
三角定規の三角比
三角定規で見かける\(\,30°\,\)、\(\,45°\,\)、\(\,60°\,\)の三角比の値は確実に記憶しておきましょう。
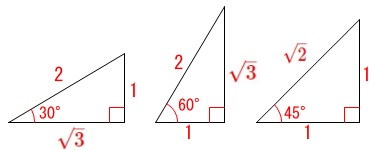 表にしておきますが、三角形を書いて比を見るようにしておいた方がいいです。
表にしておきますが、三角形を書いて比を見るようにしておいた方がいいです。
\(\begin{array}{|c|c|c|c|} \hline
\theta & \sin\theta & \cos\theta & \tan\theta \\ \hline
30^{\circ} & \displaystyle\frac{\sqrt{3}}{2} & \displaystyle \frac{1}{2} & \displaystyle \frac{1}{\sqrt{3}} \\ \hline
45^{\circ} & \displaystyle \frac{1}{\sqrt{2}} & \displaystyle \frac{1}{\sqrt{2}} & 1 \\ \hline
60^{\circ} & \displaystyle \frac{1}{2} & \displaystyle \frac{\sqrt{3}}{2} & \sqrt{3} \\ \hline
\end{array}\)
もしかしたら学校で\(\,180°\,\)までの表を覚えるように言われるかもしれません。
\(\begin{array}{|c|c|c|c|c|c|c|c|} \hline
\theta & 0^{\circ} & 30^{\circ} & 45^{\circ} & 60^{\circ} & 90^{\circ} & 120^{\circ} & 135^{\circ}& 150^{\circ} & 180^{\circ}\\ \hline
\sin\theta & & & & & & & & & \\ \hline
\cos\theta & & & & & & & & &\\ \hline
\tan\theta & & & & & & & & &\\ \hline
\end{array}\)
でも、第\(\,1\,\)象限の値から符号だけを考えれば良い状態になっておいた方が良いですよ。
三角関数になって\(\,360°\,\)までの値を覚える余裕はありません。
三角比では第\(\,2\,\)象限までです。
\(\sin\theta\,\)は第\(\,1,2\,\)象限ともに\(\,\color{red}{+}\,\)です。
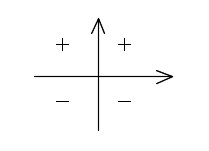
\(\cos\theta\,\)は第\(\,1\,\)象限は\(\,\color{red}{+}\,\)、第\(\,2\,\)象限は\(\,\color{blue}{-}\,\)です。
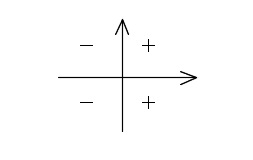
\(\tan\theta\,\)は第\(\,1\,\)象限は\(\,\color{red}{+}\,\)、第\(\,2\,\)象限は\(\,\color{blue}{-}\,\)です。
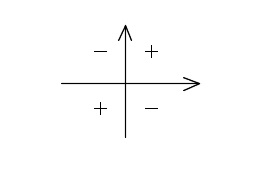 ※象限というのは軸は含まないことに注意して下さい。
※象限というのは軸は含まないことに注意して下さい。
これは「単位円」を見ながらの方が分かり易いので、
詳しいことは後の「三角比の拡張」で説明することにします。
三角比の表と読み取り方
三角比の値は角によって決まっています。
ただし、三角定規の角のようにきれいに表現できるとは限りません。
例えば、\(\,\sin 15^{\circ}=0.2588190\cdots\,\)のように無理数となります。
ここで注意しておきたいのは、
\(\hspace{10pt}\displaystyle \sin 30^{\circ}=\frac{1}{2}\)
であり、
\(\hspace{10pt}\displaystyle \sin 15^{\circ}\,\color{red}{≠}\,\frac{\sin 30^{\circ}}{2}\)
だということです。
角度が半分になることと、三角比が半分になることは一致しません。
三角比の表は教科書などの最後の方に載っています。
読み取り方は、縦に度分法の角度、横に三角比の種類となります。
\(\begin{array}{|c|c|c|c|c|} \hline
\theta & \color{blue}{\sin\theta} & \cos\theta & \tan \theta \\ \hline
0^{\circ} & \,0.0000\, & \,1.0000\, & \,0.0000\, \\ \hline
1^{\circ} & 0.0175 & 0.9998 & 0.0175 \\ \hline
\cdots & & & \\ \hline
\color{red}{15^{\circ}} & \color{magenta}{0.2588} & 0.9659 & 0.2679 \\ \hline
\cdots & & & \\ \hline
\end{array}\)
\(\hspace{10pt}\color{blue}{\sin} \color{red}{15^{\circ}}=\color{magenta}{0.2588}\)
値を覚える必要はありませんが、
たまに三角比の表が与えられる問題がありますので読み取り方は覚えておきましょう。
三角比の相互関係
三角比の定義をするときに書いた三角形は直角三角形でした。

直角三角形において三平方の定理が成り立つので、
三角比の重要な関係(公式)がいくつか得られます。
\(\color{red}{\fbox{ 公式 }}\)
\(\hspace{10pt}\color{red}{\sin^2\theta+\cos^2\theta=1}\)
\(\hspace{10pt}\displaystyle \color{red}{\tan\theta=\frac{\sin\theta}{\cos\theta}}\)
\(\hspace{10pt}\displaystyle \color{red}{1+\tan^2\theta=\frac{1}{\cos^2\theta}}\)
\(\hspace{10pt}\color{red}{\sin(\,90^{\circ}-\theta\,)=\cos\theta}\)
\(\hspace{10pt}\color{red}{\cos(\,90^{\circ}-\theta\,)=\sin\theta}\)
\(\hspace{10pt}\displaystyle \color{red}{\tan(\,90^{\circ}-\theta\,)=\frac{1}{\tan\theta}}\)
証明は図を描いて定義通りに式を立てればすぐに導けますが、
これらの関係式は無条件に覚えて下さい。
角度\(\,\theta\,\)が鋭角の場合に限らず成り立つ公式なので三角関数でも使う公式です。
三角比の拡張
三角比の定義は先にお伝えしました直角三角形を用いたものと、
原点を中心とする円を用いたものがあります。
原点中心の円を半径\(\,1\,\)の単位円に限定して定義しておきます。
\(\color{red}{\fbox{ 単位円周上の点を用いた三角比の定義 }}\)
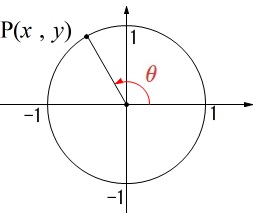
単位円\(\,x^2+y^2=1\,\)上の点\(\,\mathrm{P}(\,x\,,\,y\,)\,\)に対し
\(\,x\,\)軸の正の方向から\(\,\mathrm{OP}\,\)までの回転角を\(\,\theta\,\)とするとき、
\(\hspace{10pt}0^{\circ}\,≦\,\theta\,≦\,180^{\circ}\,\)において
\(\begin{eqnarray}\cos\theta&=&x\\
\sin\theta&=&y\\
\tan\theta&=&\frac{\sin\theta}{\cos\theta}=\frac{y}{x}\\
\end{eqnarray}\)
(ただし、\(\,x≠0\,\)とする。)
三角比では\(\hspace{4pt}0^{\circ}\,≦\,\theta\,≦\,180^{\circ}\,\)としていますが、
これは三角関数では角度が一般角となり限定されていない角でも成り立つ定義です。
単位円周上の座標は
\(\hspace{10pt}(\,x\,,\,y\,)=(\,\cos \theta\,,\,\sin \theta\,)\,\)
となるので、
\(0^{\circ}\,≦\,\theta\,≦\,180^{\circ}\,\)において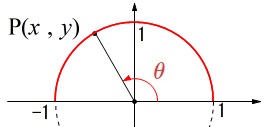
\(\,x\,\)座標が\(\,\cos\theta\,\)なので、
\(\hspace{4pt}\,-1\,≦\,\cos\theta\,≦\,1\,\)
だから\(\,\cos\theta\,\)は負(マイナス)になることはあるけど、
\(\,y\,\)座標が\(\,\sin\theta\,\)なので
\(\hspace{4pt}0\,≦\,\sin\theta\)
と\(\,\sin\theta\,\)は負の値にはならない、ということが分かります。
\(\,\theta\,\)が\(0^{\circ}\,≦\,\theta\,≦\,180^{\circ}\,\)での話です。
120°、135°、150°、180°の三角比の値
\(\,180°\,\)までの三角比を覚えている人もいると思います。
覚えておいても良いですが、
一般角まで拡張できるように第\(\,1\,\)象限の値から求められるようになっておきましょう。
例えば、\(\,\theta=60°\,\)の場合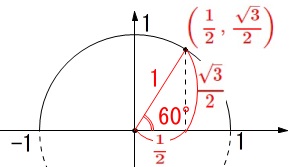
\(\hspace{10pt}\displaystyle (\,\cos 60^{\circ}\,,\,\sin 60^{\circ})=\color{red}{\left(\,\frac{1}{2}\,,\,\frac{\sqrt{3}}{2}\right)}\)
ですが、\(\,\theta=120°\,\)の場合は\(\,y\,\)軸を対称の軸として反対にあります。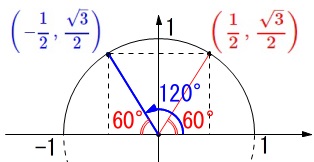
\(\hspace{10pt}\displaystyle (\,\cos 120^{\circ}\,,\,\sin 120^{\circ})=\color{blue}{\left(\,-\frac{1}{2}\,,\,\frac{\sqrt{3}}{2}\right)}\)
このとき、\(\,y\,\)座標はそのままですが\(\,x\,\)座標は正負が逆になります。
つまり、
第\(\,1\,\)象限のときと絶対値は同じだけど、符号が変化する場合がある。
ということです。
ただし、絶対値は第\(\,1\,\)象限のときと同じなので
\(\,\sin\theta\,\)は第\(\,1\,\)第\(\,2\,\)象限ともに\(\,+\,\)
\(\,\cos\theta\,\)は第\(\,1\,\)象限は\(\,+\,\)第\(\,2\,\)象限は\(\,-\,\)
\(\,\tan\theta\,\)は第\(\,1\,\)象限は\(\,+\,\)第\(\,2\,\)象限は\(\,-\,\)
と符号を変えるだけで良いのです。
これは第\(\,4\,\)象限まで同じことが言えるので符号さえ覚えておけば、
第\(\,1\,\)象限の値が一般角で使えるということです。
少し練習すればすぐに使える様になりますが、暗記が好きな人は表を覚えても良いです。笑
絶対値が同じなので次の公式が成り立ちます。
\(\color{red}{\fbox{ 補角の公式 }}\)
\(\hspace{10pt}\color{red}{\sin\,(\,180^{\circ}-\theta\,)=\sin\theta}\)
\(\hspace{10pt}\color{red}{\cos\,(\,180^{\circ}-\theta\,)=-\cos\theta}\)
\(\hspace{10pt}\color{red}{\tan\,(\,180^{\circ}-\theta\,)=-\tan\theta}\)
この公式は\(\,\theta\,\)が鈍角の三角比は、
鋭角の三角比から求めることができることを示しています。
ただし、この公式の\(\,\theta\,\)は鋭角に限られているわけではありません。
三角方程式の基本
三角方程式は三角関数で本格的に解くことになりますが、
三角比を使って方程式を解く場合と基本は同じです。
三角比の相互関係を利用して解くことになります。
注意点は、
求めるものが\(\,\sin\theta\,\)や\(\,\cos\theta\,\)ではなく
\(\,\theta\,\)であるということです。
最大値や最小値を求めるときと同じように置換することも多いですが、
ポイントは\(\,\sin \theta\,\)や\(\,\cos\theta\,\)を1つに統一することです。
三角比の相互関係は三角関数の基本であることを忘れないでください。
直線の傾きとタンジェント
\(\,2\,\)本の直線のなす角は三角関数になりますので、
ここでは原点を通る直線の傾きと\(\,x\,\)軸となす角をタンジェントで表しておきます。
一般に、
直線\(\,y=mx\,\)と\(\,x\,\)軸のなす角を\(\,\theta\,\)とすると
\(\hspace{10pt}m=\tan\theta\)
が成り立つ。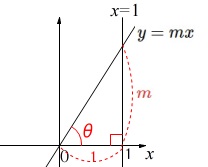 直角三角形によるタンジェントの定義そのままです。
直角三角形によるタンジェントの定義そのままです。
※
\(\,m=0\,\)のときも\(\,\tan 0^{\circ}=0\,\)なので成り立ちます。
ここまでは三角比の定義、定理の基本部分で後は三角形への応用になります。
三角比でも最大値最小値問題はありますので確認しておきましょう。
三角形への応用
三角比は三角関数の一部で、
三角形における\(\,3\,\)辺の比に関係にしたもの
として考えているくらいなのでかなり三角形へ応用できます。
代表的な定理をいくつか見ておきましょう。
後半で教科書では見かけない定理も紹介しますが使えれば使って良いです。
正弦定理
正弦定理は外接円の半径との関係式として取り上げらることが多いので、
外接円の説明からしておきます。
三角形には\(\,3\,\)頂点を通る円が1つだけ描けます。
この円を外接円といいます。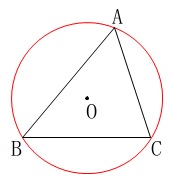 \(\,\mathrm{△ABC}\,\)の外接円の半径を\(\,R\,\)とします。
\(\,\mathrm{△ABC}\,\)の外接円の半径を\(\,R\,\)とします。
\(\color{red}{\fbox{ 正弦定理 }}\)
\(\hspace{10pt}\displaystyle \color{red}{\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}=2R}\)
(\(\,R\,\)は外接円の半径)
または、この連比を書き分けて使うこともできます。
\(\begin{eqnarray}
a&=&2R\sin A\\
b&=&2R\sin B\\
c&=&2R\sin C
\end{eqnarray}\)
さらに、注意しておきたいのが外接円の半径を抜いた関係式です。
\(\hspace{10pt}\color{red}{a:b:c=\sin A:\sin B:\sin C}\)
三角形の\(\,3\,\)辺の比が内角との比では無く、
対応する内角の正弦との比に一致するということです。
もう一つ注意点として描いておくと、
\(\hspace{10pt}A+B+C=180^{\circ}\)
であることは忘れないようにしておきましょう。
これは余弦定理のあとで例題を取り上げて説明します。
余弦定理
余弦定理には2種類あります。
さらに変形した形で使うことも多いので、余裕があればすべて覚えて使って下さい。
先ずはよく知っている余弦定理です。
\(\color{red}{\fbox{ 余弦定理 }}\)
\(\,\mathrm{△ABC}\,\)において
\(\begin{eqnarray}
a^2&=&b^2+c^2-2\,bc\cos A\\
b^2&=&c^2+a^2-2\,ca\cos B\\
c^2&=&a^2+b^2-2\,ab\cos C
\end{eqnarray}\)
この形を覚えておけば問題はありませんが、
余弦を聞かれることが多いので次の形で覚えておくと早い場合も多いです。
\(\begin{eqnarray}\displaystyle
\cos A&=&\frac{b^2+c^2-a^2}{2\,bc}\\
\cos B&=&\frac{c^2+a^2-b^2}{2\,ca}\\
\cos C&=&\frac{a^2+b^2-c^2}{2\,ab}
\end{eqnarray}\)
余弦定理を変形しただけです。
\(\color{red}{\fbox{ もう一つの余弦定理 }}\)
\(\begin{eqnarray}
a&=&b\cos C+c\cos B\\
b&=&c\cos A+a\cos C\\
c&=&a\cos B+c\cos A
\end{eqnarray}\)
これも余弦定理と呼ばれることがあります。
証明の必要も無いくらいですが、教科書には無いので簡単に1つ証明しておきます。
鋭角三角形\(\,\mathrm{ABC}\,\)において、\(\,\mathrm{A}\,\)から\(\,\mathrm{BC}\,\)に引いた垂線を\(\,\mathrm{AH}\,\)とします。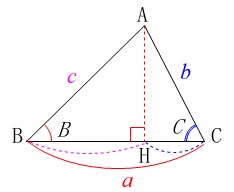
\(\,\mathrm{H}\,\)は線分\(\,\mathrm{BC}\,\)上にあるので、
\(\begin{eqnarray}
a&=&\mathrm{BC}\\
&=&\mathrm{CH+BH}\\
&=&\color{red}{b\cos C+c\cos B}
\end{eqnarray}\)
鈍角三角形\(\,\mathrm{ABC}\,\)においても同様です。
\(\,\mathrm{H}\,\)は線分\(\,\mathrm{BC}\,\)の延長上にあるので、
\(\begin{eqnarray}
a&=&\mathrm{BC}\\
&=&\mathrm{BH-CH}\\
&=&c\cos B-b\cos (\,180^{\circ}-C\,)\\
&=&c\cos B-b(-\cos C)\\
&=&c\cos B+b\cos C\\
&=&\color{red}{b\cos C+c\cos B}
\end{eqnarray}\)
正弦定理と余弦定理を手に入れたら図形で使える応用は広いですよ。
先ずは使い分けることです。
⇒ 三角形で角度が2つあるのに、正弦定理も余弦定理も使えない?
これは正弦定理の最後に描いておいた注意ですが、
\(A+B+C=180^{\circ}\)
は忘れないことです。
定理を覚えたら練習あるのみです。
正弦定理と余弦定理を応用してセットで使える様になると良いですね。
三角形の面積と三角比
三角形の面積を求める公式は算数の頃から変わりません。
\(\,△の面積=(\,底辺\,)\times (\,高さ\,)\div 2\,\)
これに正弦を加えると三角比を用いた三角形の面積になります。
\(\,\mathrm{△ABC}\,\)において底辺を\(\,\mathrm{AB}\,\)とし高さを\(\,\color{red}{h}\,\)とすると、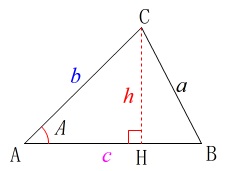
\(\displaystyle \frac{h}{b}=\sin A ⇔ \color{red}{h}=\color{red}{b\,\sin A}\)
から
\(\begin{eqnarray}
\mathrm{△ABC}&=&\frac{1}{2}\times \mathrm{AB}\times h\\
&=&\frac{1}{2}\,c\,\color{red}{b\sin A}\\
\end{eqnarray}\)
鋭角でも鈍角でも正弦の値は正なので同じ結果になりますのでまとめておきます。
\(\color{red}{\fbox{ 三角形の面積の公式 }}\)
\(\,\mathrm{△ABC}\,\)の面積を\(\,S\,\)とすると
\(\begin{eqnarray}
S&=&\frac{1}{2}\,bc\,\sin A\\
&=&\frac{1}{2}\,ca\,\sin B\\
&=&\frac{1}{2}\,ab\,\sin C
\end{eqnarray}\)
ヘロンの公式
三角形の面積の公式は基本型は先ほどの公式ですが、条件がそろえば他にもあります。
\(\,3\,\)辺を使って表すヘロンの公式そのうちの1つです。 証明は面積の公式の正弦に、
証明は面積の公式の正弦に、
三角比の相互関係と余弦定理を引用して導きます。
単なる文字式計算なので自分でやっておいて下さい。
共通テストでは試験中導くなんて時間は無くなるので覚えて使う、で良いです。
\(\color{red}{\fbox{ ヘロンの公式 }}\)
\(\,\mathrm{△ABC}\,\)の面積を\(\,S\,\)とし、\(\,3\,\)辺を\(\,a\,,b\,,\,c\,\)とする。
\(\hspace{10pt}a+b+c=2\,s\,\)
とすると
\(\hspace{10pt}\displaystyle S=\sqrt{s(\,s-a\,)(\,s-b\,)(\,s-c\,)}\)
あからさまなのであまり目立って問題にはなりませんが、
\(\,3\,\)辺が有理数で和が整数になる場合は割と使います。
特に、\(3\)辺の和が偶数のときは面積までの計算は早いですよ。
(有理数まではなんとか使えますが、時間がかかりそうな場合は避けます。笑)
内接円の半径と面積
三角形の内接の半径と面積の関係を公式にしたものがあります。
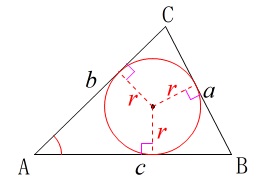
\(\color{red}{\fbox{ 公式 }}\)
\(\,\mathrm{△ABC}\,\)の内接円の半径を\(\,r\,\)とすると、
\(\hspace{10pt}\displaystyle S=\frac{1}{2}\,r(\,a+b+c\,)\)
これは内接円の半径を高さとみた三角形3つ分の和です。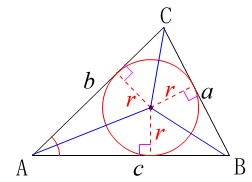 面白いのはこれからです。
面白いのはこれからです。
ヘロンの公式のときに
\(\hspace{10pt}\color{red}{a+b+c=2\,s}\)
と置きましたが、これを利用すると、
\(\begin{eqnarray}\displaystyle
S&=&\frac{1}{2}\,r(\,\color{red}{a+b+c}\,)\\
2\,S&=&r(\,\color{red}{a+b+c}\,)\\
&=&r\,\color{red}{2\,s}
\end{eqnarray}\)
これから
\(\hspace{10pt}\displaystyle \color{red}{r=\frac{S}{s}}\)
という内接円の半径が、
三角形の面積と\(\,3\,\)辺の和から求められる公式も出てきます。
(覚えなくても良いですけど、知っておいて損はありません。)
面積の公式の求め方を簡単に説明しています。
外接円の半径と面積の公式
内接円の半径と面積の公式を紹介したので、
外接円の半径と面積の公式も紹介しておきます。
\(\color{red}{\fbox{ 公式 }}\)
\(\,\mathrm{△ABC}\,\)の面積を\(\,S\,\)、外接円の半径を\(\,R\,\)とすると
\(\hspace{10pt}\displaystyle R=\frac{\,abc\,}{4\,S}\) ⇔ \(4\,SR=abc\)
証明は、正弦定理より
\(\begin{eqnarray}\displaystyle
\frac{a}{\sin A}&=&2R\\
a&=&2R\sin A\\
\color{blue}{\sin A}&=&\color{blue}{\frac{a}{2R}}
\end{eqnarray}\)
これを面積の公式に代入すると
\(\begin{eqnarray}
S&=&\frac{1}{2}\,bc\,\color{blue}{\sin A}\\
&=&\frac{1}{2}\,bc\,\color{blue}{\frac{a}{2R}}\\
&=&\frac{\,abc\,}{4R}
\end{eqnarray}\)
から簡単に導けますが、使えるかどうかはあなた次第です。笑
円に内接する四角形の面積
四角形は三角形2つでできているので四角形にも条件がそろえば使えます。
特に、四角形が円に内接する場合は対角の正弦が同じ値になるので公式があります。
\(\color{red}{\fbox{ 公式 }}\)
円に内接している四角形の4辺が\(\,a\,,\,b\,,\,c\,,\,d\,\)で
\(\hspace{4pt}2s=a+b+c+d\,\)としたとき、
内接四角形の面積を\(\,S\,\)は
\(\hspace{10pt}\displaystyle S=\sqrt{(s-a)(s-b)(s-c)(s-d)}\)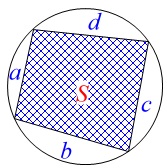
他にも三角比を利用すると証明することが簡単になることが多いです。
角の二等分線定理などもそうですが、
図形への応用は広いので基本はしっかり身に付けておきましょう。
⇒ 共通テスト(センター試験)数学の勉強法と対策まとめ単元別攻略と解説
当然のことですが共通テストでは基本が抜けていたら得点は伸びません。
大学毎に行う本試験でも同じことです。