三角比の範囲では、三角方程式の解き方はそれほど特別なものではありません。
三角関数ともなれば少しややこしいものもありますが、三角比では簡単なものばかりです。
注意点としては、求めるものを間違えないということと、解の個数を範囲内で全部数えるということです。
三角方程式とは
三角比では\(\hspace{4pt}x\hspace{4pt}\)でなく\(\hspace{4pt}\theta\hspace{4pt}\)が良く使われますが、
今回は方程式として取り上げますので\(\hspace{4pt}\sin x\hspace{4pt}\)などと表すことにします。
三角比で成り立つ方程式を三角方程式といいますが、
大切なのは求めるものは\(\hspace{4pt}\color{red}{x}\hspace{4pt}\)であるということです。
\(\hspace{4pt}\sin x\hspace{4pt}\)や\(\hspace{4pt}\cos x\hspace{4pt}\)の値ではありません。
まずは\(\,\sin x\,\)や\(\,\cos x\,\)を求めることになりますが、
その後\(\hspace{4pt}x\hspace{4pt}\)について適しているものを詳しく調べるということです。
これは他の方程式と変わりません。
問題を見ていきましょう。
(1)\(0^{\circ} \,≦\,x\,≦\,180^{\circ}\) とする。
\(2\sin^2 x+3\cos x=0\hspace{4pt}\)を解け。
(2)方程式
\(\hspace{10pt} 2\sin^2 x-\cos x-1=0\hspace{4pt}(\, 0^{\circ}\,≦\,x\,≦\, 180^{\circ})\hspace{4pt}\)
を解け。
三角方程式の解き方と注意点
三角方程式は普通の方程式とは\(\,x\,\)の範囲の指定方法がちょっと違いますが同じことですよ。
三角方程式を解くときのポイント
(1)
\(2\sin^2 x+3\cos x=0\)
のように\(\hspace{4pt}\sin x\hspace{4pt}\)と\(\hspace{4pt}\cos x\hspace{4pt}\)が混じっていると方程式が解けません。
だから先ずすることは「1つの三角比で表す」ことです。
\(\hspace{10pt} \sin^2 x+\cos^2 x=1\)
より
\(\hspace{10pt} \sin^2 x=1-\cos^2 x\)
これを与方程式に代入すると、
\(\hspace{10pt} 2(1-\cos^2 x)+3\cos x=0\)
このように\(\hspace{4pt}\cos x\hspace{4pt}\)だけ、
または\(\,\sin x\,\)だけの方程式にすることがポイントです。
後はこの方程式を\(\,\cos x\,\)について解きます。
(いきなり\(\,x\,\)ではありませんよ。)
\(\hspace{10pt} 2(1-\cos^2 x)+3\cos x=0\\ \\
\Leftrightarrow \hspace{10pt} 2-2\cos^2 x+3\cos x=0\\ \\
\Leftrightarrow \hspace{10pt} 2\cos^2 x-3cos x -2=0\\ \\
\Leftrightarrow \hspace{10pt} (2cos x+1)(\cos x-2)=0\\ \\
\Leftrightarrow \hspace{10pt} \cos x=-\displaystyle \frac{1}{2}\,, \,2\)
慣れていないうちは、\(\cos x=t\hspace{4pt}\)とでも置いて解くと、
普通の2次方程式と同じなので解きやすいです。
ここで、
\(-1\,≦\,\cos x\,≦\,1\hspace{4pt}\)より\(\,\cos x=2\,\)は不適。
だから、
\( \cos x=-\displaystyle \frac{1}{2}\)
このとき
\( 0^\circ ≦ x ≦ 180^\circ\hspace{4pt}\)において
\(\hspace{10pt}\displaystyle \cos x=-\frac{1}{2}\)
となるのは第2象限なので
\(\hspace{10pt} x=\underline{ 120^{\circ} }\)
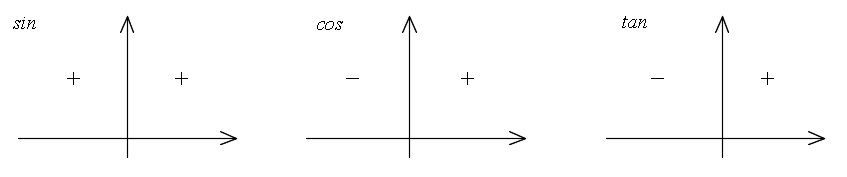
三角比の象限による正負
\( \color{red}{0^\circ ≦ x ≦ 180^\circ}\,\)では
\( \color{red}{-1≦ \cos x ≦ 1}\,\)であり\(\,\color{red}{0≦ \sin x ≦ 1}\,\)です。
(\(\,\tan x\,\)については上限下限はありませんが、定義域が途切れるところがあります。)
(2)
\( 2\sin^2 x-\cos x-1=0\)
についても\(\hspace{4pt}\sin x\hspace{4pt}\)か\(\hspace{4pt}\cos x\hspace{4pt}\)かのどちらかに統一しましょう。
もちろん\(\hspace{4pt}\sin^2 x=1-\cos^2 x\hspace{4pt}\)から\(\hspace{4pt}\cos x\hspace{4pt}\)に統一します。
\(\hspace{10pt} 2\sin^2 x-\cos x-1=0\\
\Leftrightarrow \hspace{10pt} 2(1-\cos^2 x)-\cos x-1=0\\
\Leftrightarrow \hspace{10pt} 2-2\cos^2 x-\cos x-1=0\\
\Leftrightarrow \hspace{10pt} 2\cos^2 x+\cos x-1=0\\
\Leftrightarrow \hspace{10pt} (2\cos x-1)(\cos x+1)=0\\
\Leftrightarrow \hspace{10pt} \cos x=\displaystyle \frac{1}{2}\,,\,-1\)
\( 0^\circ ≦ x ≦ 180^\circ\hspace{4pt}\)において
\(\hspace{10pt}\displaystyle\cos x=\frac{1}{2}\hspace{4pt}\)
のとき
\(\hspace{4pt} x=60^\circ\hspace{4pt}\)(1つだけ)
\(\hspace{10pt} \cos x=-1\hspace{4pt}\)
のとき
\(\hspace{4pt} x=180^\circ\)
よって、
\(\hspace{10pt} x=\underline{ 60^\circ \,,\,180^\circ }\)
(両方が解です。)
\( 0^\circ ≦ x ≦ 180^\circ\hspace{4pt}\)では、
\( \sin x\hspace{4pt}\)が負になることはありませんが\(\hspace{4pt}\cos x\hspace{4pt}\)はあります。
このように\(\,\sin x\,\)や\(\,\cos x\,\)の値を出して、
その後、条件に合う\(\,x\,\)を探し出す、ということです。
三角比で作られた式の値を求める計算問題もあります。
こちらと合わせて基本問題は落とさないようにしておきましょう。
応用問題はこれらができてからです。
最大値最小値はどこでも出てきます。
三角関数につながる基本なので要点は少ないですが、
図形への応用はかなり広いです。