三角比で使う定理と公式は、正弦定理、余弦定理、面積の公式です。
定理の使い方や解き方は問題の中で説明しますので確認しておいてください。
また、内接円や外接円の半径や面積問題が付いてきますが大したポイントではありません。
重要なことが他にありますのでしっかり目を通しておいてください。
三角比と切り離せない三角形と図形
三角比の問題は計算だけでなく、必ずといって良いほど「図形」がからんできます。
だから「幾何」は同時に対策した方が良いのですが、
ここでは『図は書きましょう!』ということだけをお伝えし、
正弦定理、余弦定理と面積の公式それと少し外接円、内接円を説明します。
忘れないでください。
三角形の3辺の比に関連しているから「三角比」と呼ばれるのです。
問題を見ておきましょう。
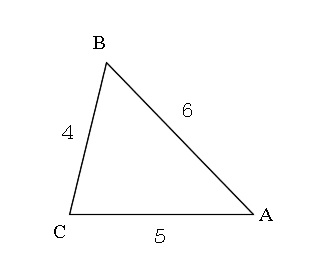
\(\,\mathrm{△ABC}\,\)において、\( a=4\,,\,b=5\,,\,c=6\hspace{4pt}\)である。
\( \cos A\hspace{4pt},\hspace{4pt}\sin A\hspace{4pt}\)および\(\,\mathrm{△ABC}\,\)の面積を求めよ。
また、\(\,\mathrm{△ABC}\,\)の内接円の半径、および外接円の半径を求めよ。
角度が1つも与えられていないので余弦定理を使う可能性が大きいです。
後で確認してみましょう。
先ず、\(\,\mathrm{△ABC}\,\)と言うとき、
頂点は大文字、辺は小文字で表し、
\( \mathrm{BC}=a\,,\,\mathrm{CA}=b\,,\,\mathrm{AB}=c\)
と各頂点の対辺を小文字で示すことが習慣です。
問題に何も書いていないというのは少ないですが、
\(\mathrm{BC}=a\hspace{4pt}\)と書いていなくても、
「辺\(\,a\,\)は\(\,\angle A\,\)の対辺」
だと考えてください。
それを念頭に置いて2つの定理を書き出しておきます。
正弦定理と余弦定理
証明は教科書にあると思いますので省略します。
【正弦定理】
\(\large{\displaystyle\frac{a}{\sin A}=\frac{b}{\sin B}=\frac{c}{\sin C}=2R}\)
( \( R\) は外接円の半径)
【余弦定理】(第2)
\(\large{\color{red}{a^2=b^2+c^2-2bc\cos A}}\)
\(\large{\color{red}{b^2=c^2+a^2-2ca\cos A}}\)
\(\large{\color{red}{c^2=a^2+b^2-2ab\cos A}}\)
(3つのうち1つ覚えれば辺と角の位置関係は同じです。)
この余弦定理は、
\(\hspace{10pt}a^2=b^2+c^2-2bc\cos A\)
を変形すると
\(\hspace{10pt}\large{\displaystyle \cos A=\frac{b^2+c^2-a^2}{2bc}}\)
となりますが、
この形でもよく使うので覚えておくといちいち変形する必要がなく時間の節約にはなります。
何度も練習問題を解いて行くうちに覚えてしまうことが多いですけどね。
では問題に入りましょう。
「\(\hspace{4pt}\cos A\hspace{4pt},\sin A\hspace{4pt}\)および\(\,\mathrm{△ABC}\,\)の面積を求めよ。」
三角比の問題では、図を書くことは当然の作業として、
「正弦定理」、「余弦定理」「面積の公式」
は使うものと考えておいていいです。
「三角比の問題」と気がついたら問題を解き始める前に公式を書き出しておいて、
大問の序盤でちょっとでも悩んだら「使っていない定理はないか?」と確認してみると良いことあります。
答えを出しておきましょう。
余弦定理から、
\(\begin{eqnarray}\displaystyle
\cos A&=&\frac{b^2+c^2-a^2}{2bc}\\
&=&\frac{5^2+6^2-4^2}{2\cdot 5 \cdot 6}\\
&=&\frac{3}{4}
\end{eqnarray}\)
これから
\(\hspace{10pt} \sin^2 A+\cos^2 A=1\)
を利用して
\(\begin{eqnarray}\displaystyle
\sin^2 A&=&1-\cos^2 A\\
\sin^2 A&=&1-\left( \frac{3}{4}\right)^2\\
&=& \frac{7}{16}
\end{eqnarray}\)
ここで\(\,\sin \,>\,0\,\)より
\(\hspace{10pt}\displaystyle \sin A=\frac{\sqrt{7}}{4}\)
面積の公式より
\(\begin{eqnarray}\displaystyle
S&=&\frac{1}{2}\,bc \sin A\\
&=&\frac{1}{2}\times 5\times 6\times \frac{\sqrt{7}}{4}\\
&=&\frac{15\sqrt{7}}{4}
\end{eqnarray}\)
と、ここまでは出来る人は多いでしょう。
というよりもう飽きるほど学校でやってきたと思います。(他もそうですが)
次に面積の公式を確認しますが、その前に、もう一つ数学の習慣をお伝えしておきます。
外接円の半径は「 \(\color{red}{R}\) 」で表し、
内接円の半径は「 \(\color{blue}{r}\) 」で表すことが普通です。
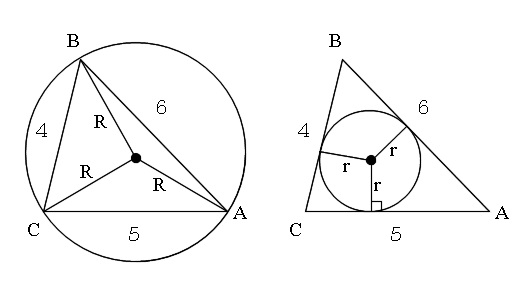
問題にはふつう書いてありますが、覚えておいてください。
当サイトではできるだけその都度説明を書きますが、抜けているときは察してください。w
面積の公式
すでに三角比で習う面積の公式を使って答えを出していますが、
内接円の半径で表される面積の公式も合わせて確認しておきましょう。
小学生で習う三角形の面積
\(\color{red}{(三角形の面積)=(底辺)\times(高さ)\div 2}\)
これが基本公式です。
中学生だと(底辺)を\(\hspace{4pt}c\hspace{4pt}\)とし、(高さ)を\(\hspace{4pt}h\hspace{4pt}\)とすると、
面積\(\,S\,\)は
\(\hspace{10pt}\large{\color{red}{\displaystyle S=\frac{1}{2}\,ch}}\)
と記号を使って表します。
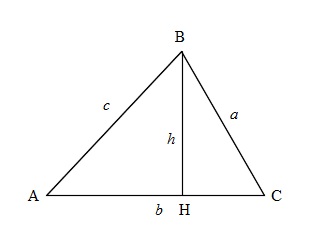
これに三角比を引用すると
\(\displaystyle\sin A=\frac{\color{red}{h}}{b} \hspace{10pt} \Leftrightarrow \hspace{10pt}\color{red}{h}=b\sin A\)
だから
\(\begin{eqnarray}\displaystyle
S&=&\frac{1}{2}\,c\,\color{red}{h}\\
&=&\frac{1}{2}\,bc\,\sin A
\end{eqnarray}\)
と面積の公式が導けます。
他の角についても同様に成り立ちます。
【面積の公式】
\(\begin{eqnarray}\displaystyle
S&=&\frac{1}{2}\,bc\,\sin A\\
&=&\frac{1}{2}\,ca\sin B\\
&=&\frac{1}{2}\,ab\sin C
\end{eqnarray}\)
ところで面積の公式はこれだけではありません。
他にもいろいろとありますが、図形(幾何)と合わせて中学生でも良く使う公式を紹介しておきます。
\(\,\mathrm{△OAB}\,\)において内心(内接円の中心)を\(\,\mathrm{O}\,\)とすると
\(\,\mathrm{AB\,⊥\,OC}\,\)
なので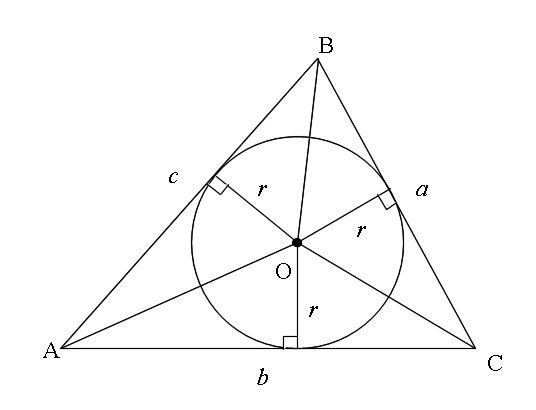
内接円の半径を\(\hspace{4pt}r\hspace{4pt}\)とすると、
\(\,\mathrm{△OAB}\,\)の面積\(\, S_\mathrm{OAB}\,\)は
\(\hspace{10pt}\displaystyle S_\mathrm{OAB}=\frac{1}{2}\,cr\)
( 底辺\(\,c\,\)高さ\(\,r\,\))
\(\,\mathrm{△ABC}\,\)は\(\,\mathrm{△OAB}\,\)と\(\,\mathrm{△OAC}\,\)と\(\,\mathrm{△OCB}\,\)を合わせたものなので
\(\begin{eqnarray} \displaystyle
S_\mathrm{ABC}&=&S_\mathrm{OAB}+S_\mathrm{OAC}+S_\mathrm{OCB}\\
&=&\frac{1}{2}\,cr+ \frac{1}{2}\,br+ \frac{1}{2}\,ar\\
&=& \frac{1}{2}\,r(\,a+b+c\,)
\end{eqnarray}\)
これが三角形の\(\,3\,\)辺と内接円の半径との関係を用いた面積の公式です。
【内接円の半径と面積】
\(\hspace{10pt}\large{\color{red}{\displaystyle S_\mathrm{ABC}=\frac{1}{2}(a+b+c)r}}\)
問題の後半は「\(\,\mathrm{△ABC}\,\)の内接円の半径,および外接円の半径を求めよ。」です。
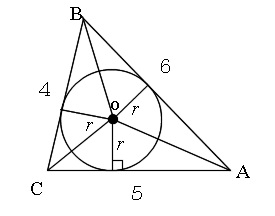
内接円は三角形に内接していますが、
三角形から見れば\(\,\mathrm{△ABC}\,\)は内接円に外接していることになります。
つまり、
三角形の各辺は内接円の接線
となっているのです。
(半径は各辺に垂直になっているということです。)
だから内接円の半径は、図において、
\(\,\mathrm{△AOB,△BOC,△COA}\,\)の高さと言えます。
\(\,\mathrm{△ABC=△AOB+△BOC+△COA}\,\)
なので、
先程求めた面積
\(\displaystyle S=\frac{15\sqrt{7}}{4}\)
を利用すると
\(\begin{eqnarray}\displaystyle
S&=&\frac{1}{2}\,(\,6r+4r+5r\,)\\
&=&\color{red}{\frac{15\,r}{2}=\frac{15\sqrt{7}}{4}}
\end{eqnarray}\)
より
\(\hspace{10pt} r=\displaystyle \frac{\sqrt{7}}{2}\)
と求まります。
外接円の半径は正弦定理より、
\(\begin{eqnarray}\displaystyle
\frac{a}{\sin A}&=&2R \\
a&=&2\,R\sin A\\
R&=&\displaystyle \frac{a}{2\sin A}
\end{eqnarray}\)
ここで\(\,\sin A=\displaystyle \frac{\sqrt{7}}{4}\,\)は求めているの、
\(\begin{eqnarray}\displaystyle
R&=&\frac{a}{\color{red}{2\sin A}}\\
&=&4 \div \left(\color{red}{2\cdot \frac{\sqrt{7}}{4}}\right)\\
&=&4\times \frac{2}{\sqrt{7}}\\
&=&\frac{8\sqrt{7}}{7}
\end{eqnarray}\)
正弦定理は覚えている人は多いでしょう。
内接円の半径\(\,r\,\)についての面積の公式
\(\hspace{10pt} S=\displaystyle \frac{1}{2}(a+b+c)r\)
も覚えておいた方が良いですよ。
長くなるので正弦定理と余弦定理の使い分けについては
別に取り上げることにします。
正弦定理や余弦定理を使うときは図形がからんできます。
手を抜かないで、必ず図を書くことはしましょう。
他にも定理、公式はたくさんあります。
