三角比の問題だとわかっても、正弦定理と余弦定理の使い分けで迷うときがありますよね。
どちらでもできるということがありますので断言はできませんが問題の見分け方の基準を示しておきます。
迷うくらいならどちらもやって見る、それでもかまいませんよ。
かかる時間の問題ですが解けないよりはマシです。
この基準を覚えられたとき、「どちらを使えば良いか」の判断はすでにできていることになります。
正弦定理を使う場合
どちらの定理を使うにしても三角形を指定される問題がほとんどです。
その中で「角度が1つでも与えられている」ことが最低条件です。
三平方の定理が成り立つ「直角三角形」は例外で、中学生の問題以外はなかなかありません。
角度が1つも与えられていない場合、先ずは余弦定理定理を試してください。
さらに条件を絞ると、
与えられた角度に対し、対辺が与えられているときに正弦定理が使えます。
例えば、
「\(\,\mathrm{△ABC}\,\)において、
\(\mathrm{B}=30^\circ\hspace{4pt},\hspace{4pt}b=\mathrm{CA}=1\hspace{4pt},\hspace{4pt}c=\mathrm{AB}=\sqrt{3}\hspace{4pt}\)であるという。
\( a=\mathrm{BC}\hspace{4pt}\)と頂角\(\hspace{4pt}\mathrm{A}\hspace{4pt},\hspace{4pt}\mathrm{C}\hspace{4pt}\)を求めよ。」
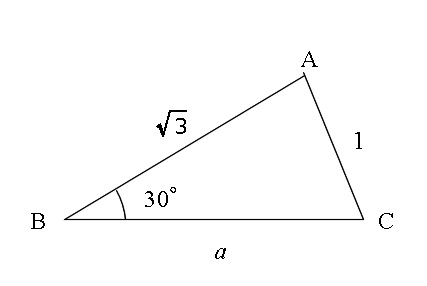
この問題は\(\,\mathrm{∠B}\,\)に対する辺\(\,b\,\)が与えられているので正弦定理が使えます。
余弦定理を使って
\(\hspace{4pt} 1^2=a^2+(\sqrt{3})^2-2\sqrt{3}a \cos 30^\circ\)
とすることもできます。
ここでは解きませんが、この場合\(\,a\,\)は2つ出てきます。
答えも2通り出てきますから注意してください。
正弦定理を使うと頂角\(\,\mathrm{C}\,\)が先に求まり、
余弦定理を使うと辺\(\,a\,\)が先に求まります。
正弦定理を優先して使う場合は、
角度が1つとその対辺がわかっている場合、
角度が2つ(ということは3つ)わかっている場合、
ということです。
もちろん、限定するという意味ではありませんよ。
上の問題のように余弦定理でも解けるものもあるのです。
余弦定理を使う場合
角度が1つも与えられていないときは迷わず余弦定理を使って下さい。
ただし、どの角度が有名角で具体的な角度が出てくるかは試して見るしかありません。
正弦定理のところで取り上げた問題も余弦定理は使えました。
角度が与えられている場合でも余弦定理が使えないわけではありません。
正弦定理の方がはやい、
ということはありますが余弦定理の方が使えるところは多いです。
余弦定理が使えないのは最低2辺がわかっていないときです。
2辺がわかっていればもう一つの辺は文字を使って表せば定理が使えます。
このときも1つは角度、または\(\,\cos\,\)の値は必要になりますので注意して下さい。
問題に辺が1つしかない場合は正弦定理を使うことが多く、
2辺以上わかっている場合は余弦定理が使える場合が多い、
ということです。
条件次第なので、断定しているわけではないことは了承ください。
解かなくて良いですが、次の問題はどちらを使うか選んでみて下さい。
「\(\,\mathrm{△ABC}\,\)において、次の値を求めよ。
(1) \( \mathrm{B}=45^\circ\,,\,b=2\,,\,c=\sqrt{6}\hspace{4pt}\)のとき頂角\(\,\mathrm{A,C}\,\)の値。
(2) \( \mathrm{A}=60^\circ\,,\,b=4\,,\,c=3\hspace{4pt}\)のとき\(\,a\,\)の値。」
(1)は与えられた角の対辺もわかるので正弦定理。
(2)は与えられた角の対辺がわからないので余弦定理。
と判断して良いでしょう。
(1)に余弦定理はちょっと嫌な感じですね。
1つだけ言わせて下さい。
「△」「三角形」と図形を表す用語が問題にあって、
図を書かないというのは、
「解く気が無い」
と判断されてもおかしくありませんよ。
「図が書けない」、というのは次のような問題のときです。
正弦定理か余弦定理か?判断できるかの確認問題と解き方
では問題を1つ解いておきましょう。
\(\,\mathrm{△ABC}\,\)の内角の大きさを\(\,\mathrm{A\,,\,B\,,\,C}\,\)
その対辺を\(\,a\,,\,b\,,\,c\,\)とする。
\(\hspace{10pt} (a+b):(b+c):(c+a)=4:5:6\)
のとき、\(\,\mathrm{C}\,\)の大きさを求めよ。
角度は与えられていないので余弦定理を使います。
ところで、
連比では定石がありました。
連比では比の値が一定なので文字で置き換える方法です。
\(\hspace{10pt} (a+b):(b+c):(c+a)=4:5:6\\
\displaystyle \Leftrightarrow \hspace{4pt}\frac{a+b}{4}=\frac{b+c}{6}=\frac{c+a}{5}=\color{red}{k} ・・・☆\)
とおく。
すると
\( \begin{cases}
\hspace{4pt}a+b=4k ・・・(1)\\
\hspace{4pt}b+c=6k ・・・(2)\\
\hspace{4pt}c+a=5k ・・・(3)\end{cases}\)
これらを辺々加えると、
\(\hspace{10pt} 2(a+b+c)=15k\)
となり
\(\hspace{10pt}\displaystyle a+b+c=\frac{15}{2}k\)
これから(1),(2)、(3)をそれぞれ引くと、
\(c\,,\,a\,,\,b\,\)がそれぞれ\(\,k\,\)で表せます。
しかし、\(\,a\,,\,b\,,\,c\,\)が\(\,k\,\)を使った分数になるので、
\(\,☆\,\)の時点で、“ \(\hspace{4pt}\color{red}{=2k}\hspace{4pt}\)” とおいておくと、
\( \begin{cases}
\hspace{4pt}a+b=8k ・・・(1)’\\
\hspace{4pt}b+c=12k ・・・(2)’\\
\hspace{4pt}c+a=10k ・・・(3)’\end{cases}\)
(1)’~(3)’の辺々加えると、
\(\begin{eqnarray}
2(a+b+c)&=&30k\\
a+b+c&=&15k\end{eqnarray}\)
これから(1)’(2)’(3)’を引くと整数係数のまま処理できます。
分数のままでも良いのですが計算を楽にするちょっとしたコツです。
\(\hspace{10pt}a+b+c=15k\)
から(1)’(2)’(3)’をそれぞれ辺々引くと、
\(\hspace{4pt} c=7k \hspace{4pt},\hspace{4pt}a=3k \hspace{4pt},\hspace{4pt} b=5k\)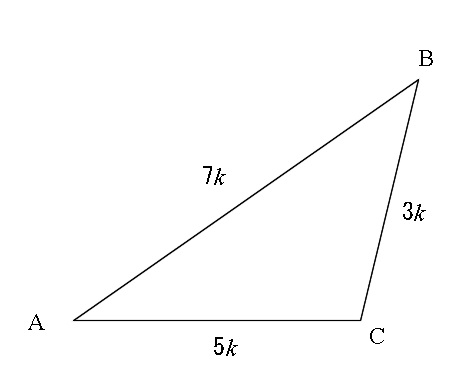
さて、
「なんでこんなことをやってんだ?」
と思っている人もいるでしょう。
問題は「\(\,\mathrm{C}\,\)の大きさを求めよ。」です。
余弦定理ですね。
しかし、各辺が分かっていないので
\(\hspace{10pt}\,4:6:5\,\)
という比のままの値を長さとしても答えは出るのですが、
一般的な場合で成り立つことを示すためです。
\(\begin{eqnarray}\displaystyle
\cos \mathrm{C}&=& \frac{a^2+b^2-c^2}{2ab}\\
&=& \frac{(3k)^2+(5k)^2-(7k)^2}{2\cdot 3k\cdot 5k}\\
&=& \frac{9k^2+25k^2-49k^2}{30k^2}\\
&=& \frac{-15\,k^2}{30\,k^2}\\
&=&-\frac{1}{2}
\end{eqnarray}\)
このように\(\,k\,\)は必ず消えます。
よって
\(\hspace{10pt} \mathrm{C}=\underline{ 120^\circ }\)
すべてが比でおかれている(具体的な数値ではない)ので、
\(a=3\hspace{4pt},\hspace{4pt}b=5\hspace{4pt},\hspace{4pt}c=7\)
として余弦定理を使っても同じ結果ですが、
限定しているので十分性がありません。
マーク(答えだけ出すなら)では良いけど、記述のときは注意して下さい。
この問題はある程度計算を進めないと図の特長をとらえにくいです。
長さが1つもありませんからね。
ただ、比の和を比べて\(\,c\,>\,b\,>\,a\,\)は推測できるので大まかな図を書いておくくらいで良いです。
計算を進めてわかってきたことを図に書き込む、という作業はやっておきましょう。
三角比において
「角度」「等式の証明」「三角形の形状」
などの問題は、
正弦定理、余弦定理などを用いて、
『辺』だけ、または『角のみの含む関係』
に持ち込むと都合良く進む場合が多いです。
正弦定理か余弦定理かすぐに判断できないときは、
余弦定理優先で良いかもしれませんが、「どちらもやって見る」といいですね。
どちらかしか使ってはいけない、ということはありません。
定理、公式は覚えて使えるようになっておくことが先で良いですよ。
三角比の相互関係から見直しておきましょう。