ベクトル方程式による面積比の問題と解き方

ベクトル方程式によって表される点の位置と三角形の面積比の問題の解き方です。
点の位置はベクトルをあつかう際の基本通りで良いことを問題の解き方を見ながら確認しておきましょう。
処理が終われば面積比については中学の図形の知識があれば十分です。

ベクトル方程式とは

ベクトル方程式とは、ベクトルで図形を表した方程式のことです。
当たり前のことをいっているので分かりにくいかもしれませんね。

例えば、
中心が原点で半径　\(r\)　の円を座標系で表すと

　\( x^2+y^2=r^2\)
となりますよね。
これをベクトル方程式で表すと、
原点中心で半径　\( r\)　の円周上の点\(\,\mathrm{P}\,\)とを結ぶベクトルを　\( \overrightarrow{\mathrm{OP}}\)　とすると

　\(\hspace{10pt} \displaystyle \color{red}{|\overrightarrow{\mathrm{OP}}|=r}\)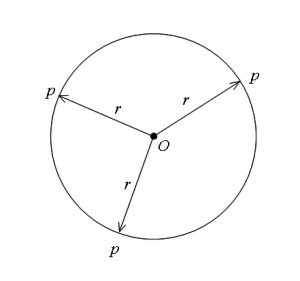
とベクトルを用いて、
　「中心と円周上の点との距離が一定」、
という円の定義に基づいたベクトルの関係式で表せるのです。

このような方程式をベクトル方程式といいます。

ただ、「ベクトル方程式とは何か？」を考えるより、
ベクトル方程式があって、何が言えるか？の方が大切ですよ。
はっきり言ってベクトル方程式なんて言葉は後回しでもいいくらいです。

ベクトル方程式を１からやるのは長くなるので、
ちょっとした有名問題を取り上げて説明します。

ベクトル方程式を扱う例題

実は、
　正の数　\( k　,　l　,　m\)　において
　\( \color{red}{k}\,\overrightarrow{\mathrm{PA}}+\color{red}{l}\,\overrightarrow {\mathrm{PB}} +\color{red}{m}\,\overrightarrow{\mathrm{PC}}=\overrightarrow{0}\)
　が成り立つとき、

　\(\hspace{10pt} \mathrm{\triangle PBC:\triangle PAC:\triangle PAB}=\color{red}{k:l:m}\)

になると分かっているので、

　\(\hspace{10pt} \mathrm{\triangle ABC=\triangle PBC+ \triangle PAC+ \triangle PAB}\)

より

　\(\hspace{10pt} \mathrm{\triangle ABC:\triangle PBC}\\
=(2+3+4):2\\
=9:2\)

と答えだけならすぐに出せます。

ですが、ベクトルの基本的な処理方法に沿っていけば、知らなくても答えが出せるということを示しておきます。

ベクトルをあつかうときの基本

平面ベクトルをあつかうときの基本は、
　「始点を１つにする」
　「２つの独立なベクトルで表す」
をできるだけ徹底することです。

　\(\hspace{10pt} \mathrm{2\overrightarrow{PA}+3\overrightarrow {PB} +4\overrightarrow{PC}}=\overrightarrow{0}\)

は始点はそろっているように見えますが、３つのベクトルで成り立っています。

ちょっとわかりにくいかもしれません。
\(\,\mathrm{△ABC}\,\)と\(\,\mathrm{△PBC}\,\)の面積比較なので、
「\(\,\mathrm{△ABC}\,\)があって」どこかに「点\(\,\mathrm{P}\,\)がある」と考えると、
始点を\(\,\mathrm{A}\,\)として　\(\overrightarrow{\mathrm{AB}}\)　と　\( \overrightarrow{\mathrm{AC}}\)　の２つで表せば良いのではないかと考えたわけです。

△の位置関係から\(\,\mathrm{A}\,\)を始点に換え、
\(\,\mathrm{\overrightarrow{AP}}\,\)を\(\,\mathrm{\overrightarrow {AB}\,,\,\overrightarrow{AC}}\,\)で表します。

　\(\hspace{10pt} \mathrm{2\overrightarrow{PA}+3\overrightarrow {PB} +4\overrightarrow{PC}}=\overrightarrow{0}\\ \\
\Leftrightarrow \hspace{5pt} -2\overrightarrow{\mathrm{AP}}+3(\overrightarrow {\mathrm{AB}}- \overrightarrow{\mathrm{AP}})+4(\overrightarrow{\mathrm{AC}}-\overrightarrow{\mathrm{AP}})=\overrightarrow{0}\\ \\
\Leftrightarrow \hspace{5pt} \mathrm{-9\overrightarrow{AP}+3\overrightarrow {AB}+4\overrightarrow{AC}}=\overrightarrow{0}\\ \\
\Leftrightarrow \hspace{5pt} \mathrm{9\overrightarrow{AP}=3\overrightarrow {AB}+4\overrightarrow{AC}}\\ \\
\Leftrightarrow \hspace{5pt} \mathrm{\overrightarrow{AP}=\displaystyle \frac{3}{9}\overrightarrow {AB}+\displaystyle \frac{4}{9}\overrightarrow{AC}}\)

（ベクトルでは約分せず分母を同じにしておくと比があつかいやすくなります。）

\(\,\mathrm{AP}\,\)を延長して\(\,\mathrm{BC}\,\)との交点\(\,\mathrm{Q}\,\)までを考えれば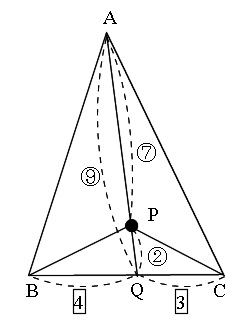
　\( \begin{eqnarray}\displaystyle
\overrightarrow{\mathrm{AP}}&=& \frac{7}{9}\left( \frac{3}{7}\overrightarrow {\mathrm{AB}}+ \frac{4}{7}\overrightarrow{\mathrm{AC}}\right)\\
&=& \frac{7}{9}\,\overrightarrow{\mathrm{AQ}}
\end{eqnarray}\)

と変形できて

　\(\hspace{10pt} \mathrm{AP:PQ=7:2}\)

底辺は共通しているので
　\(\hspace{10pt}\mathrm{△ABC：△PBC=9:2}\)
と答えは同じように出てきます。

上のベクトル方程式の変形をメンドウだと思う人はベクトルは捨てても良いです。
始点をそろえるという作業がメンドウに感じるならベクトルは無理です。

２つのベクトルの終点を結ぶ直線上にある条件

　\(\begin{eqnarray} \displaystyle
\overrightarrow{\mathrm{AP}}&=& \frac{3}{9}\overrightarrow {\mathrm{AB}}+ \frac{4}{9}\overrightarrow{\mathrm{AC}}\\
&=& \frac{7}{9}\left( \mathrm{\frac{3}{7}\overrightarrow {AB}+ \frac{4}{7}\overrightarrow{AC}}\right)
\end{eqnarray}\)

の変形が難しいと感じるかもしれませんが、

　\(\displaystyle \mathrm{\overrightarrow{AP}= \frac{3}{9}\overrightarrow {AB}+ \frac{4}{9}\overrightarrow{AC}}\)
なので、点\(\,\mathrm{Q}\,\)は\(\,\mathrm{AP}\,\)の延長にあるから実数倍して、

　\(\begin{eqnarray}\displaystyle
\overrightarrow{\mathrm{AQ}}&=&k\,\overrightarrow{\mathrm{AP}}\\
&=&k\,\left( \mathrm{\frac{3}{9}\overrightarrow {AB}+ \frac{4}{9}\overrightarrow{AC}}\right)
\end{eqnarray}\)

とおくことができます。

また、\(\,\mathrm{Q}\,\)は\(\,\mathrm{BC}\,\)上の点（２つのベクトルの終点を結ぶ直線上の点）だから

　\(\displaystyle \frac{3}{9}k+\frac{4}{9}k=1\)　より　\(\displaystyle k=\frac{9}{7}\)　と出せば、

　\( \begin{eqnarray}\displaystyle
\overrightarrow{\mathrm{AQ}}&=& \frac{9}{7}\overrightarrow{\mathrm{AP}}\\
&=& \mathrm{\frac{9}{7}\left( \frac{3}{9}\overrightarrow {AB}+ \frac{4}{9}\overrightarrow{AC}\right)}\\
&=& \mathrm{\frac{3}{7}\overrightarrow {AB}+ \frac{4}{7}\overrightarrow{AC}}
\end{eqnarray}\)
（係数の和\(\displaystyle \frac{3}{7}+\frac{4}{7}=1\)が成り立つことを確認できます。）

そして、
　\(\begin{eqnarray}\displaystyle
\overrightarrow{\mathrm{AQ}}&=& \frac{9}{7}\overrightarrow{\mathrm{AP}}\\ \\
⇔　 \overrightarrow{\mathrm{AP}}&=& \frac{7}{9}\overrightarrow{\mathrm{AQ}}
\end{eqnarray}\)

となることから、
　\(\displaystyle \mathrm{\overrightarrow{AP}= \frac{7}{9}\left( \frac{3}{7}\overrightarrow {AB}+ \frac{4}{7}\overrightarrow{AC}\right)}\)

とすることはそれほど難しいことではない、と思うのですが、難しいですか？
ここまでができない高校生が多いのは事実です。

２つのベクトルの終点を結ぶ直線上の点\(\,\mathrm{P}\,\)において、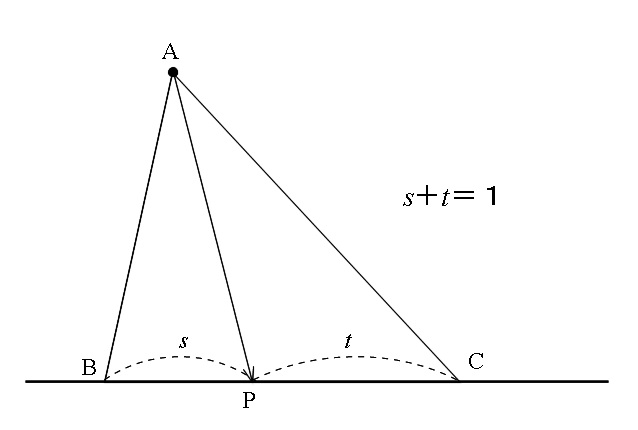
　\(\hspace{10pt} \overrightarrow {\mathrm{AP}}= \color{red}{s}\overrightarrow {\mathrm{AB}}+ \color{red}{t}\overrightarrow {\mathrm{AC}}\)
の係数の関係　\( \color{red}{s+t=1}\)　がうまく使えていないだけなのでしっかり復習しておきましょう。

さて、最初に書いた

　\(\hspace{10pt} k\,\overrightarrow{\mathrm{PA}}+l\,\overrightarrow {\mathrm{PB}} +m\,\overrightarrow{\mathrm{PC}}=\overrightarrow{0}\)

が成り立つとき、

　\(\hspace{10pt} \mathrm{\triangle PBC:\triangle PAC:\triangle PAB}=k:l:m\)

を確認してみます。

　\( \mathrm{\triangle ABC=9}\)　のとき　\( \mathrm{\triangle PBC=2}\)　でした。

　\(\hspace{10pt} \mathrm{BQ:QC=4:3} \\
\Leftrightarrow \hspace{5pt} \mathrm{\triangle ABQ:\triangle ACQ=4:3}\)

なので、
　\(\hspace{10pt}\displaystyle \color{red}{\mathrm{\triangle ACQ}}= \frac{3}{7}\times 9= \color{red}{\frac{27}{7}}\)

　\(\hspace{10pt} \displaystyle\color{blue}{ \mathrm{\triangle ABQ}}= \frac{4}{7}\times 9= \color{blue}{\frac{36}{7}}\)

であり、
　\(\begin{eqnarray}\displaystyle
\triangle \mathrm{PAC}&=&\triangle \color{red}{\mathrm{ACQ}} \times \frac{7}{9}\\
&=&\color{red}{\frac{27}{7}}\times \frac{7}{9}\\
&=&3
\end{eqnarray}\)

　\(\begin{eqnarray}\displaystyle
\triangle \mathrm{PAB}&=&\color{blue}{\triangle \mathrm{ABQ}} \times \frac{7}{9}\\
&=&\color{blue}{\frac{36}{7}}\times \frac{7}{9}\\
&=&4
\end{eqnarray}\)

となり、

　\(\hspace{10pt} \mathrm{2\overrightarrow{PA}+3\overrightarrow {PB} +4\overrightarrow{PC}}=\overrightarrow{0}\)

を満たすとき、確かに

　\(\hspace{10pt} \mathrm{\triangle PBC:\triangle PAC:\triangle PAB}=2:3:4\)

となっていますね。

係数の値と三角形の位置がどう対応するのかですが、

\(\,\mathrm{P}\,\)で三角形を三分割したとき

　\(\hspace{10pt} \overrightarrow{\mathrm{PA}}\)　の係数は、\(\,\mathrm{A}\,\)を含んでいない三角形
　\(\hspace{10pt} \overrightarrow{\mathrm{PB}}\)　の係数は、\(\,\mathrm{B}\,\)を含んでいない三角形
　\(\hspace{10pt}\overrightarrow{\mathrm{PC}}\)　の係数は、\(\,\mathrm{C}\,\)を含んでいない三角形

に対応します。図で確認して下さい。
（点\(\,\mathrm{P}\,\)が\(\,\mathrm{△ABC}\,\)の外にあるときは自分で研究してみてください。）

この関係式は覚えておく必要はないけど、
ベクトルを使えるようになりたければ導けるようにはなっておいた方が良いかもしれませんよ。

ベクトルも基本が大切です。

⇒　平面ベクトルの要点

つまずいたら、基本からやり直すことが結局は近道になります。