空間のベクトルの要点です。
空間における点の座標からベクトルの成分、内積、方程式や図形との関係をまとめます。
平面ベクトルで定義や定理はまとめてあるのでここでは成分を1つ増やした程度で済ませます。
空間の点
空間における点は、平面における点と同じです。
大きさもない単なる点ですが、位置を定めるために座標を用います。
空間の点の座標
簡単に言ってしまえば空間では座標が1つ増えます。
\(\,xy\,\)平面に上下の位置をもたするために軸が1つ増えるのです。
この三つ目の軸を\(\,z\,\)軸といいます。
\(\color{red}{\fbox{ 空間の座標系 }}\)
空間の\(\,1\,\)点\(\,\mathrm{O}\,\)で直交する\(\,3\,\)直線をとり、
それぞれに\(\,\mathrm{O}\,\)を原点とする目盛りを入れ数直線とする。
これら\(\,3\,\)本の数直線を\(\,x\,\)軸、\(\,y\,\)軸、\(\,z\,\)軸と名付ける。
3つの軸を総称して座標軸という。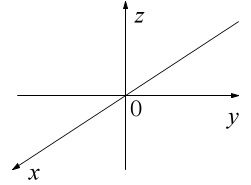
\(\,x\,\)軸、\(\,y\,\)軸、\(\,z\,\)軸は順に反時計回りに設定するのが習慣です。
\(\color{red}{\fbox{ 空間の点の座標 }}\)
原点\(\,\mathrm{O}\,\)から\(\,x\,\)軸、\(\,y\,\)軸、\(\,z\,\)軸のそれぞれの正の向きに
\(\,a\,,\,b\,,\,c\,\)だけ平行移動した点\(\,\mathrm{P}\,\)の座標を
\(\hspace{10pt}(\,a\,,\,b\,,\,c\,)\)
と表し、\(\,a\,,\,b\,,\,c\,\)をそれぞれ点\(\,\mathrm{P}\,\)の
\(\hspace{10pt}x\,座標 , y\,座標 , z\,座標\,\)という。
座標が\((\,a\,,\,b\,,\,c\,)\)の点を、
\(\hspace{10pt}点(\,a\,,\,b\,,\,c\,)\,\)と書く。
平面のときと同じルールです。
\(\color{red}{\fbox{ 座標平面 }}\)
\(\,x\,\)軸、\(\,y\,\)軸を含む平面を\(\,xy\,\)平面という。
\(\,y\,\)軸、\(\,z\,\)軸を含む平面を\(\,yz\,\)平面という。
\(\,z\,\)軸、\(\,x\,\)軸を含む平面を\(\,zx\,\)平面という。
これらを座標平面とよぶ。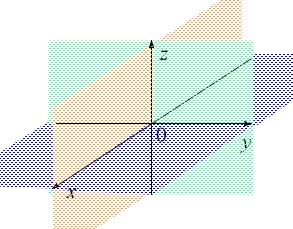
座標平面がどこなのかはよく見ておきましょう。
座標を定められた空間を座標空間といいます。
\(\color{red}{\fbox{ 空間座標における原点との距離 }}\)
原点\(\,\mathrm{O}\,\)と点\(\,\mathrm{P}(\,a\,,\,b\,,\,c\,)\,\)の距離は
\(\hspace{10pt}\displaystyle \mathrm{OP}=\sqrt{\,a^2+b^2+c^2\,}\)
これは平面の原点からの距離に\(\,z\,\)成分が増えただけで、
中学校の頃に計算した直方体の対角線の長さと同じです。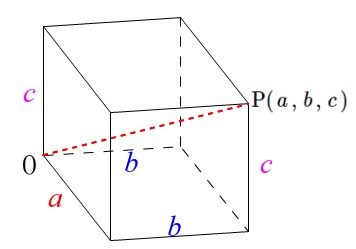
空間座標は平面座標に\(\,z\,\)成分が増えただけ、と考えて良いです。
しかし、図示するとなるとかなり位置関係がつかみにくいので、
ある程度の位置関係が分かれば、座標上の視覚には頼らない方が良いかもしれません。
空間のベクトル
空間のベクトルも有効線分がベクトルを表すということは同じです。
空間ベクトルの表し方
空間でも始点を\(\,\mathrm{A}\,\)終点を\(\,\mathrm{B}\,\)とするベクトルとその大きさを
\(\hspace{10pt}\,ベクトルを\mathrm{\overrightarrow{AB}}\,,\,大きさを|\mathrm{\overrightarrow{AB}}|\)
と表します。
逆ベクトルや零（ゼロ）ベクトルおよび単位ベクトルの定義も全く同じです。
忘れている人は平面ベクトルからやり直してください。
ここで同じことを説明すると長くなるだけで、あなたの時間が無駄になるだけです。
空間ベクトルの分解
平面ベクトルは2つのベクトルに分解できました。
空間では3つに分解することになります。
座標空間でいえば、\(\,z\,\)成分が加わるからですね。
ただし、3つに分けるのは軸に平行な単位ベクトルだけではありません。
それを説明するために平行六面体について説明しておきます。
\(\color{red}{\fbox{ 平行六面体 }}\)
2つずつ平行な、3組の平面で囲まれる立体を平行六面体という。
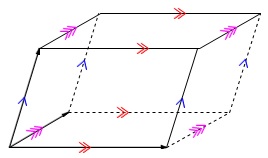座標平面で作られる直方体も平行六面体に含まれます。
平行六面体において、
1つの頂点からできる3つのベクトルを同一平面に置かないとき、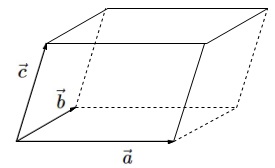
その3つのベクトルを\(\,\vec{a}\,,\,\vec{b}\,,\,\vec{c}\,\)とすると
\(\hspace{10pt}\vec{p}=s\,\vec{a}+t\,\vec{b}+u\,\vec{c}\)
は実数\(\,s\,,\,t\,,\,u\,\)を適当に決めることで空間すべての点を表すことができます。
さらに、平面同様1つの点\(\,\mathrm{P}\,\)に対し、\(\,s\,,\,t\,,\,u\,\)の組はただ1つに定まります。
空間でも
\(\hspace{10pt}s\,\vec{a}+t\,\vec{b}+u\,\vec{c}\)
は線型結合とよばれます。
※
3つのベクトルを同一平面に置かないとは、
始点と終点となる3つの4点が同一平面に無いということです。
つまり、平面では2つのベクトル、
空間では3つのベクトルを用いてすべての点が表せる
ということです。
始点を\(\,\mathrm{O}\,\)とすることが多いので同一平面にない4点を
\(\,\mathrm{O\,,\,A\,,\,B\,,\,C}\,\)
\(\,\overrightarrow{\mathrm{OA}}=\vec{a}\,,\,\overrightarrow{\mathrm{OB}}=\vec{b}\,,\,\overrightarrow{\mathrm{OC}}=\vec{c}\)
としてまとめておきます。
\(\color{red}{\fbox{ 空間ベクトルの線型独立 }}\)
3つの空間ベクトル\(\,\vec{a}\,,\,\vec{b}\,,\,\vec{c}\,\)が線型独立である条件は
4点\(\,\mathrm{O\,,\,A\,,\,B\,,\,C}\,\)が同一平面にないことである。
\(\,\vec{a}\,,\,\vec{b}\,,\,\vec{c}\,\)は\(\,\vec{0}\,\)ではない、という条件を含みます。
\(\color{red}{\fbox{ 係数の一意性 }}\)
空間のベクトル\(\,\vec{a}\,,\,\vec{b}\,,\,\vec{c}\,\)が線型独立ならば、
任意の空間ベクトル\(\,\vec{p}\,\)は実数\(\,s\,,\,t\,,\,u\,\)を用いて
\(\hspace{10pt}\vec{p}=s\,\vec{a}+t\,\vec{b}+u\,\vec{c}\)
の形でただ一通りに表される。
\(\,\vec{p}\,\)を決めれば\(\,s\,,\,t\,,\,u\,\)は決まり、
\(\,s\,,\,t\,,\,u\,\)を決めれば\(\,\vec{p}\,\)は定まる、
ということです。
これが空間ベクトルを扱うとき、基底を3つにすると良い、という理由です。
空間ベクトルの成分
何度もいっていますが空間ベクトルの成分は\(\,z\,\)成分が増えるだけです。
空間ベクトルの成分表示
平面ベクトルと同じなので簡単にまとめます。
\(\color{red}{\fbox{ 基本ベクトル }}\)
\(\,x\,\)軸、\(\,y\,\)軸、\(\,z\,\)軸の正の向きと同じ向きの単位ベクトルを
基本ベクトルといい、それぞれ\(\,\vec{e_1}\,,\,\vec{e_2}\,,\,\vec{e_3}\,\)
と表す。
また、
\(\hspace{10pt}\overrightarrow{\mathrm{OA}}=\,\vec{a}=(\,a_1\,,\,a_2\,,\,a_3\,)\,\)
で表される点\(\,\mathrm{A}\,\)が基本ベクトルを用いて
\(\hspace{10pt}\vec{a}=a_1\vec{e_1}+a_2\vec{e_2}+a_3\vec{e_3}\)
のように線形結合で表せることも同じです。
\(\,\,a_1\,,\,a_2\,,\,a_3\,\,\)がそれぞれ\(\,x\,\)成分、\(\,y\,\)成分、\(\,z\,\)成分です。
\(\color{red}{\fbox{ 大きさ }}\)
\(\,\vec{a}=(\,a_1\,,\,a_2\,,\,a_3\,)\,\)の大きさは
\(\hspace{10pt}\displaystyle |\,\vec{a}\,|=\sqrt{\,a_1^2\,+a_2^2\,+a_3^2\,}\)
これも\(\,z\,\)成分が増えただけで、二点間の距離と同じです。
\(\color{red}{\fbox{ ２点を結ぶベクトルと大きさ }}\)
\(\,2\,\)点\(\,\mathrm{A}(\,a_1\,,\,a_2\,,\,a_3\,)\,\)、\(\,\mathrm{B}(\,b_1\,,\,b_2\,,\,b_3\,)\)において、
\(\hspace{10pt}\overrightarrow{\,\mathrm{AB}\,}=(\,b_1-a_1\,,\,b_2-a_2\,,\,b_3-a_3\,)\)
\(\hspace{10pt}\displaystyle |\overrightarrow{\,\mathrm{AB}\,}|=\sqrt{(b_1-a_1)^2+(b_2-a_2)^2+(b_3-a_3)^2\,}\)
始点を原点とすれば大きさはいつも同じ計算をすれば求まります。
\(\color{red}{\fbox{ 和と実数倍 }}\)
和
\(\hspace{10pt}(\,a_1\,,\,a_2\,,\,a_3\,)+(\,b_1\,,\,b_2\,,\,b_3\,)\\
=(\,a_1+b_1\,,\,a_2+b_2\,,\,a_3+b_3\,)\)
差
\(\hspace{10pt}(\,a_1\,,\,a_2\,,\,a_3\,)-(\,b_1\,,\,b_2\,,\,b_3\,)\\
=(\,a_1-b_1\,,\,a_2-b_2\,,\,a_3-b_3\,)\)
実数倍
\(\hspace{10pt}k\,(\,a_1\,,\,a_2\,,\,a_3\,)\\
=(\,ka_1\,,\,ka_2\,,\,ka_3\,)\)
各成分の和、差、実数倍になります。
紙面を取るので教科書では横ベクトルが多いですけど、
\(\begin{eqnarray}
\left(
\begin{array}{c}
x \\
y \\
x \\
\end{array}
\right)
\end{eqnarray}\)
のように縦ベクトルで計算すると空間ベクトルは見やすいです。
\(\begin{eqnarray}
\left(
\begin{array}{c}
a_1 \\
a_2 \\
a_3 \\
\end{array}
\right)
+
\left(
\begin{array}{c}
b_1 \\
b_2 \\
b_3 \\
\end{array}
\right)
=
\left(
\begin{array}{c}
a_1 +b_1\\
a_2 +b_2\\
a_3 +b_3\\
\end{array}
\right)
\end{eqnarray}\)
各成分を横に見るだけなのでミスが減ります。
もちろん、平面ベクトルでも使えますよ。
空間ベクトルの内積
内積の定義と定理も平面と同じです。
内積の定義と定理
\(\color{red}{\fbox{内積の定義}}\)
\(\,\vec{0}\,\)でないベクトル\(\,\vec{a}\,,\,\vec{b}\,\)のなす角を\(\,\theta\,\)とすると
\(\hspace{10pt}\vec{a}\cdot \vec{b}=|\vec{a}||\vec{b}|\cos\theta\)
これは\(\,\vec{a}=\vec{0}\,\)または\(\,\vec{b}=\vec{0}\,\)のときも成り立ちます。
\(\hspace{10pt}\vec{a}\cdot \vec{b}=0\)
しかし、余り\(\,\vec{0}\,\)について内積を扱わないので、
内積が\(\,0\,\)になるときは垂直条件だと考えることが圧倒的に多いです。
\(\color{red}{\fbox{ 内積の定理 }}\)
\(\,\vec{0}\,\)でない\(\,\vec{a}=(\,a_\,,\,a_2\,,\,a_3\,)\,,\,\vec{b}=(\,b_\,,\,b_2\,,\,b_3\,)\,\)のなす角を\(\,\theta\,\)とする。
\(\hspace{10pt}\vec{a}\cdot \vec{b}=a_1b_1+a_2b_2+a_3+b_3\)
また、なす角\(\,\theta\,\)は定義と合わせて
\(\begin{eqnarray}\displaystyle
\cos\theta&=&\frac{\vec{a}\cdot \vec{b}}{|\vec{a}||\vec{b}|}\\
&=&\frac{a_1b_1+a_2b_2+a_3+b_3}{\sqrt{a_1^+a_2^2+a_3^2}\sqrt{b_1^2+b_2^2+b_3^2}}
\end{eqnarray}\)
空間ベクトルの垂直条件
\(\color{red}{\fbox{ 垂直条件 }}\)
\(\,\vec{0}\,\)でない\(\,\vec{a}=(\,a_\,,\,a_2\,,\,a_3\,)\,,\,\vec{b}=(\,b_\,,\,b_2\,,\,b_3\,)\,\)において
\(\hspace{10pt}\vec{a}\,\)⊥\(\,\vec{b}\,\) ⇔ \(\vec{a}\cdot\vec{b}=0\)
成分で表せば
\(\hspace{10pt}\vec{a}\,\)⊥\(\,\vec{b}\,\) ⇔ \(a_1b_1+a_2b_2+a_3b_3\)
平面と同じ定義、同じ定理が成り立つので分けて考えなくて良いです。
ベクトルの空間図形への応用
ここまで来れば、平面と空間で違うのは成分が1つ増えること、というのは分かったでしょう。
位置ベクトルと一直線上にある点の条件
空間の位置ベクトル、一直線上にある点の条件も平面と同じです。
ただし、座標空間で図示すると位置関係を示すことが非常にやっかいなのでベクトルの性質を使って計算で解決させることが多くなります。
図示することは非常に重要な作業ですが、空間だけは大まかに位置関係が見て取れれば良し、としておいた方が良いかもしれません。
平面と空間で少し違うのが同じ平面上にある点の条件です。
同じ平面上にある点の条件
平面ベクトルで、定点\(\,\mathrm{O}\,\)に対し、
\(\,\overrightarrow{\mathrm{OA}}=\vec{a}\,,\,\overrightarrow{\mathrm{OB}}=\vec{b}\)
とすると、
\(\hspace{10pt}\vec{p}=s\,\vec{a}+t\,\vec{b}\,,\,\color{red}{s+t=1}\)
となる点\(\,\mathrm{P}\,\)は直線\(\,\mathrm{AB}\,\)上の点になるというのがありました。
空間でも同様の定理がありますが二通りの表現ができます。
\(\color{red}{\fbox{ 同じ平面にある点 }}\)
一直線上にない\(\,3\,\)点\(\,\mathrm{A}(\vec{a})\,,\,\mathrm{B}(\vec{b})\,,\,\mathrm{C}(\vec{c})\,\)で定まる平面\(\,\mathrm{ABC}\,\)上に、
点\(\,\mathrm{P}(\vec{p})\,\)があるとき、
\(\hspace{10pt}\overrightarrow{\mathrm{CP}}=s\,\overrightarrow{\mathrm{CA}}+t\,\overrightarrow{\mathrm{CB}}\)
となる\(\,s\,,\,t\,\)がひと組決まる。
逆に、\(\,s\,,\,t\,\)をひと組決めれば点\(\,\mathrm{P}\,\)は1つ固定される。
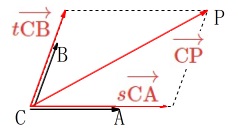これは\(\,\mathrm{C}\,\)を始点としているので,
\(\hspace{10pt}\overrightarrow{\mathrm{CA}}\,,\,\overrightarrow{\mathrm{CB}}\)
の2つのベクトルで作られる平面\(\,\mathrm{ABC}\,\)から\(\,\mathrm{P}\,\)が外れることはありません。
これを始点が平面\(\,\mathrm{ABC}\,\)の外にある点でも成り立つように位置ベクトルを使って変形します。
位置ベクトルを用いて変形すると
\(\begin{eqnarray}
\overrightarrow{\mathrm{CP}}&=&s\overrightarrow{\mathrm{CA}}+t\overrightarrow{\mathrm{CB}}\\
\vec{p}-\vec{c}&=&s\,(\,\vec{a}-\vec{c}\,)+t\,(\,\vec{b}-\vec{c}\,)\\
\vec{p}&=&s\,\vec{a}+t\,\vec{b}+(\,1-s-t\,)\,\vec{c}
\end{eqnarray}\)
ここで、\(\,1-s-t=u\,\)とすると
\(\hspace{10pt}\vec{p}=s\,\vec{a}+t\,\vec{b}+u\,\vec{c}\,,\,\color{red}{s+t+u=1}\)
が成り立ちます。
\(\color{red}{\fbox{ 同じ平面にある点その２ }}\)
\(\,\mathrm{△ABC}\,\)と空間の任意の点\(\,\mathrm{O}\,\)について
\(\hspace{10pt}\overrightarrow{\mathrm{OP}}=s\,\overrightarrow{\mathrm{OA}}+t\overrightarrow{\mathrm{OB}}+u\overrightarrow{\mathrm{OC
}}\)
かつ
\(\hspace{10pt}s+t+u=1\)
で表される点\(\,\mathrm{P}\,\)は平面\(\,\mathrm{ABC}\,\)上にある。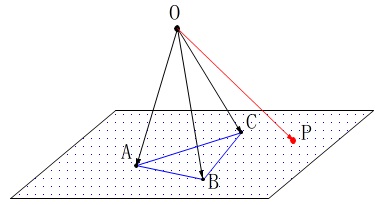
3つの線型独立な空間ベクトルの終点を通る平面上の点の条件です。
\(\,s\,,\,t\,,\,u\,\)を適当に決めることで空間すべての点を表すことができるので、
空間ベクトルでは始点を1つに、基底を3つで表すことを基本にしておけば良いのです。
平面は空間内にありますが、視覚（直感）的に抜き出しにくい場合もあります。
しかし、ベクトルの性質を利用すれば式で処理できるので慣れておくと便利ですよ。
座標空間における図形の表し方
方程式はちょっと違いますが他の項目は平面と同じです。
何度同じことをいっているのでしょうか？笑
２点間の距離と内分点外分点の座標
\(\color{red}{\fbox{ 2点間の距離 }}\)
2点\(\,\mathrm{A}(\,a_1\,,\,a_2\,,\,a_3\,)\,,\,\mathrm{B}(\,b_1\,,\,b_2\,,\,b_3\,)\,\)において
\(\,\mathrm{A,B}\,\)間の距離は
\(\hspace{10pt}\displaystyle \mathrm{AB}=\sqrt{(b_1-a_1)^2+(b_2-a_2)^2+(b_3-a_3)^2\,}\)
これはベクトルの大きさに等しいのですでに説明してありますね。
\(\color{red}{\fbox{ 線分ＡＢを内分する点 }}\)
線分\(\,\mathrm{AB}\,\)を\(\,m:n\,\)に内分する点の座標は
\(\hspace{10pt}\displaystyle \left(\,\frac{na_1+mb_1}{m+n}\,,\,\frac{na_2+mb_2}{m+n}\,,\,\frac{na_3+mb_3}{m+n}\right)\)
線分\(\,\mathrm{AB}\,\)を\(\,m:n\,\)に外分する点の座標は
\(\hspace{10pt}\displaystyle \left(\,\frac{-na_1+mb_1}{m-n}\,,\,\frac{-na_2+mb_2}{m-n}\,,\,\frac{-na_3+mb_3}{m-n}\right)\)
線分\(\,\mathrm{AB}\,\)の中点の座標は
\(\hspace{10pt}\displaystyle \left(\,\frac{a_1+b_1}{2}\,,\,\frac{a_2+b_2}{2}\,,\,\frac{a_3+b_3}{2}\right)\)
外分は\(\,m:(-n)\,\)に内分、中点は\(\,1:1\,\)に内分と形式的にみれば良いだけですね。
ベクトルで\(\displaystyle \,\vec{p}=\frac{n\vec{a}+m\vec{b}}{m+n}\)と内分することに成分を当てはめただけです。
座標平面に平行な平面の方程式
座標平面は、
\(\,x\,\)軸に垂直な\(\,yz\,\)平面（\(\,x=0\,\)）
\(\,y\,\)軸に垂直な\(\,zx\,\)平面（\(\,y=0\,\))
\(\,z\,\)軸に垂直な\(\,xy\,\)平面（\(\,z=0\,\)）
があります。
これらは原点を通る平面です。
軸\(\,x\,,\,y\,,\,z\,\)に垂直だけど原点を通らない平面の方程式を示しておきます。
座標平面に平行な平面の方程式です。
\(\color{red}{\fbox{ 座標平面に平行な平面の方程式 }}\)
点\(\,\mathrm{A}(\,a\,,\,0\,,\,\,)\,\)を通り、\(\,yz\,\)平面に平行な平面の方程式は \(\,x=a\,\)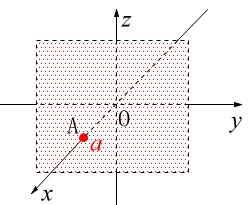
簡易的な図で切り取ってますが平面はどこまでも伸びています。
それと、\(\,x=a\,\)という平面では
「\(\,y\,,\,z\,\)成分は？」
と思うかもしれませんので説明しておくと、
\(\,y\,,\,z\,\)は任意です。
（何でも良い、すべての実数で成り立つ、ということです。）
平面\(\,x=a\,\)を
\(\,x=a\,(\,y,z\,は任意)\,\)
と表しても構いませんが、
空間座標であることあることが明らかで条件が何もない場合は、
\(\,(\,y,z\,は任意)\,\)ということは書いてあることと同じ意味になるので\(\,x=a\,\)だけで良いのです。
逆に言えば、空間座標において\(\,y\,,\,z\,\)について条件が何もなく、
\(\,x=a\,\)と書かれてあればそれは平面を表していると見なさなければなりません。
「平面\(\,x=a\,\)」と書いてあるのが普通ですけどね。
点\(\,\mathrm{A}\,\)は\(\,x\,\)軸との交点だから\(\,y=z=0\,\)なので
\(\,(\,a\,,\,0\,,\,0\,)\,\)
と\(\,y\,,\,z\,\)に条件がつきます。
同様に、
点\(\,\mathrm{B}(0\,,\,b\,,\,0\,)\,\)を通り、\(\,zx\,\)平面に平行な平面の方程式は\(\,y=b\,\)
点\(\,\mathrm{C}(0\,,\,0\,,\,c\,)\,\)を通り、\(\,xy\,\)平面に平行な平面の方程式は\(\,z=c\,\)
となります。
これは、平面の方程式から自分でイメージした図を描いてみておいてください。
座標平面のどれと平行になるのかを実感しておきましょう。
一般の平面の方程式
これは現行の教科書では発展内容で奥が深いところになるので説明するとものすごく長くなります。
私が好きな項目でもあるからなおさらです。笑
なので簡単に済ませておきます。
1つの平面があれば、必ずその平面に垂直なベクトルが存在します。
これを法線ベクトルといいます。
垂直という条件だけなので大きさはいろいろありますが、
平面上のどこの点でとっても方向は同じです。
そして、この法線ベクトルは平面上のすべてのベクトルと垂直でもあります。
平面上で任意の異なる\(\,2\,\)点を取ってできるどのベクトルとも垂直だということですよ。
※
これは直線と平面が垂直であるときの大切なことなので良く問題に組み込まれているのですが、
中学生だけでなく高校生でもよく分かっていない人が多いです。
\(\color{red}{\fbox{ 平面のベクトル方程式 }}\)
定点\(\,\mathrm{P_0}\,\)を通り、法線ベクトル\(\,\vec{n}\,\)である平面のベクトル方程式は
\(\hspace{10pt}\color{red}{\vec{n}\cdot (\,\vec{p}-\vec{p_0}\,)=0}\)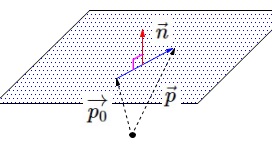
これに成分を与えます。
\(\color{red}{\fbox{ 成分による平面の方程式 }}\)
点\(\,\mathrm{P_0}\,(\,x_0\,,\,y_0\,,\,x_0\,)\,\)を通り、
法線ベクトルベクトル\(\,\vec{n}=(\,a\,,\,b\,,\,c\,)\,\)とする平面の方程式は
\(\hspace{10pt}a\,(\,x-x_0\,)+b\,(\,y-y_0\,)+c\,(\,z-z_0\,)=0\)
この方程式は展開して定数項をまとまると
\(\hspace{10pt}\color{red}{ax+by+cz+d=0}\)
となり、法線ベクトルを\(\,\vec{n}\,\)とする平面すべてを表しています。
ただし、\(\,a\,,\,b\,,\,c\,\)の少なくとも1つは\(\,0\,\)ではありません。
学校でも空間ベクトルを習うとき、
「2つのベクトルの両方に垂直な（単位）ベクトルを求めよ。」
という問題に遭遇して、「メンドクサイ計算」と感じたことあると思うのですが、笑
あれは法線ベクトルの1つ（または2つ）を求めているに過ぎません。
簡単に求める方法はありますが説明が長くなるのでここでは省略します。
もちろん、知っている人はジャンジャン使って良いですよ。（解答の裏側で。笑）
面積にまで利用できるともっといい。
空間における直線の方程式
直線は平面と同じ表示ができます。
\(\color{red}{\fbox{ 空間における直線のベクトル方程式 }}\)
定点\(\,\mathrm{P_0}\,\)を通り、方向ベクトル\(\,\vec{u}\,\)である直線のベクトル方程式は
媒介変数\(\,t\,\)を用いて
\(\hspace{10pt}\color{red}{\vec{p}=\overrightarrow{p_0}+t\,\vec{u}}\)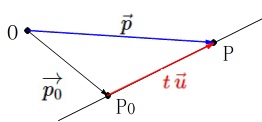
教科書にはありませんが、\(\,\mathrm{O\,,\,P_0\,,\,P}\,\)は1つの平面にあるので直感的に平面の場合と同じだと、感じてください。笑
※
すべての教科書に目を通した訳ではありませんので、見逃してたら「教科書にある。」と読み取ってください。
これに成分を与えます。
\(\hspace{10pt}\vec{p}=\overrightarrow{p_0}+t\,\vec{u}\)
において
\(\,\vec{p}=(\,x\,,\,y\,,\,z\,)\,\)
\(\,\vec{p_0}=(\,x_0\,,\,y_0\,,\,z_0\,)\,\)
\(\,\vec{u}=(\,a\,,\,b\,,\,c\,)\,\)
とおくと、媒介変数表示できます。
\( \begin{cases}
\hspace{7pt} x=x_0+a\,t\\
\hspace{7pt} y=y_0+b\,t\\
\hspace{7pt} z=z_0+c\,t
\end{cases}\)
この媒介変数\(\,t\,\)を消去すると直線の方程式が出てきます。
\(\color{red}{\fbox{ 成分を用いた空間における直線の方程式 }}\)
定点\(\,\mathrm{P_0}=(\,x_0\,,\,y_0\,,\,z_0\,)\,\)を通り、
方向ベクトル\(\,\vec{u}=(\,a\,,\,b\,,\,c\,)\)である直線の方程式は
\(\hspace{10pt}\displaystyle \color{red}{\frac{x-x_0}{a}=\frac{y-y_0}{b}=\frac{z-z_0}{c}}\)
ただし、これは
\(\,a\,\)≠\(\,0\,\)、\(\,b\,\)≠\(\,0\,\)、\(\,c\,\)≠\(\,0\,\)のとき、
または、分母が\(\,0\,\)のときは分子も\(\,0\,\)であるといえるとき、
という条件付きです。
この直線の方程式を使いこなせるようになると、
空間における交点問題はかなり楽になります。
余裕があれば使いこなしましょう。
以前は教科書にあった内容です。
⇒ 空間ベクトルで点から下ろした垂線と平面との交点を求める方法
最近でもよく見かける問題ですね。
アロー（矢印）ベクトルだけでなく、成分を設定して使って解くのも面白いですよ。
球面の方程式
これは教科書にあります。笑
\(\color{red}{\fbox{ 球のベクトル方程式 }}\)
定点\(\,\mathrm{C}(\vec{c})\,\)を中心、
半径を\(\,r\,\)とする球面にある点\(\,\mathrm{P}(\vec{p})\,\)のベクトル方程式は
\(\hspace{10pt}\,|\,\vec{p}-\vec{c}\,|=r\,\)
円の定義にベクトルを当てはめただけですね。
これに座標を与えます。
\(\vec{p}=(\,x\,,\,y\,,\,x\,)\)
\(\vec{c}=(\,x_0\,,\,y_0\,,\,x_0\,)\)
とすると、二点間の距離の公式を経て、
\(\hspace{10pt}(x-x_0)^2+(y-y_0)^2+(z-z_0)^2\,=r^2\)
を得ることができます。
\(\color{red}{\fbox{ 球の方程式 }}\)
点\(\,(\,x_0\,,\,y_0\,,\,z_0\,)\,\)を中心とする半径\(\,r\,\)の球の方程式は
\(\hspace{10pt}(x-x_0)^2+(y-y_0)^2+(z-z_0)^2\,=r^2\)
以上です。
平面の方程式、直線の方程式、球の方程式を連立することでいろいろな交点が求められるようになりました。
存分にベクトルを楽しんでください。
平面と空間は定義、定理はほとんど変わりません。
なので、もう一度平面からベクトルを見直しておくと良いです。
共通テストでもセンター試験でも平面ベクトルだった、空間ベクトルだった、という必要はなくなります。