空間ベクトルで要となる問題ともいえる、同一平面上にある条件を求める問題を解説します。
ベクトルの成分を使った解き方と、平面の方程式を使ったとき方の両方を示しておきますので可能なら使って下さい。
空間図形を苦手にしているのは中学生だけではなく高校生にも多くいますが、原因は難しいからではありません。
空間ベクトルを使うときの基本
空間ベクトルと平面ベクトルの違いは、基底となるベクトルの数です。
平面ベクトルは、２つの線型独立なベクトル
\(\vec {a} , \vec{b} (\vec{a} \neq 0 , \vec{b} \neq 0 , \vec{a}∦\vec{b})\)
（互いに平行でもなく、それぞれは０でもない）
で平面上のすべての点\(\,\mathrm{P}\,\)が表せました。
\(\hspace{10pt}\vec{p}=s\vec{a}+t\vec{b}\)
空間ではこの基底となるベクトルが３つになります。
３つの線型独立なベクトル \(\vec {a} , \vec{b} , {c}\) を用いて
\(\hspace{10pt} \vec{p}=s\vec{a}+t\vec{b}+u\vec{c}\)
と空間内のすべての点\(\,\mathrm{P}\,\)が表せます。
ただ、同一平面上にあるなら、基底とするベクトルは空間でも２つで良いのです。
問題で見てみましょう。
空間ベクトルが同一平面上にある条件
\( \mathrm{P}\,(1\,,\,3\,,\,2)\,,\,\mathrm{Q}\,(2\,,\,1\,,\,2)\,,\,\mathrm{R}\,(4\,,\,4\,,\,1)\,,\,\mathrm{S}\,(m\,,\,m-1\,,\,4)\)
が同一平面上にあるとき、\( m\) の値を求めよ。
空間では基本的には、基底とするベクトルを３つとします。
しかし、ここでは４点が「同一平面上」にあるということから、
平面と同じく２つの基底ベクトル \(\overrightarrow{\mathrm{PQ}} , \overrightarrow{\mathrm{PR}}\) で
\( \mathrm{\overrightarrow{PS}}\) が表せます。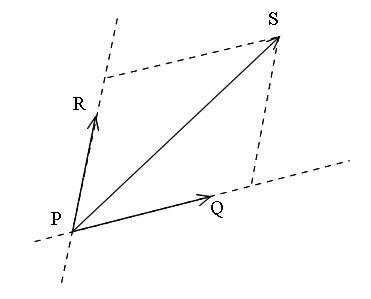
平面で少しは慣れたと思うので、いきなりですが、
\(\hspace{10pt}\mathrm{\overrightarrow{PS}=\color{red}{\alpha} \,\overrightarrow{PQ}+\color{blue}{\beta} \,\overrightarrow{PR}}\)
となる実数 \( \color{red}{\alpha} , \color{blue}{\beta}\) が存在します。
このように表すと、点 \( S\) の \( m\) も含めて文字が３つになりますが、
空間座標では成分が３つあるので、連立することで解くことができるのです。
縦ベクトルと横ベクトル
先に \( \overrightarrow{\mathrm{PS}}\) と \( \overrightarrow{\mathrm{PQ}}\) と \( \overrightarrow{\mathrm{PR}}\) を座標で表しておきましょう。
\(\begin{eqnarray} \overrightarrow{\mathrm{PS}}&=&\overrightarrow{\mathrm{OS}}-\overrightarrow{\mathrm{OP}}\\
&=&\left(\begin{array}{c} m \\
m-1 \\
4 \end{array} \right)
-\left(\begin{array}{c} 1 \\
3 \\
2 \end{array} \right)\\
&=&\left(\begin{array}{c} m-1 \\
m-4 \\
2 \end{array} \right)
\end{eqnarray}\)
\(\begin{eqnarray} \overrightarrow{\mathrm{PQ}}&=&\mathrm{\overrightarrow{OQ}-\overrightarrow{OP}}\\
&=&\left(\begin{array}{c} 2 \\
1 \\
2 \end{array} \right)
-\left(\begin{array}{c} 1 \\
3 \\
2 \end{array} \right)\\
&=&\left(\begin{array}{c} 1 \\
-2 \\
0 \end{array} \right)
\end{eqnarray}\)
\(\begin{eqnarray} \overrightarrow{\mathrm{PR}}&=&\mathrm{\overrightarrow{OR}-\overrightarrow{OP}}\\
&=&\left(\begin{array}{c} 4 \\
4 \\
1 \end{array} \right)
-\left(\begin{array}{c} 1 \\
3 \\
2 \end{array} \right)\\
&=&\left(\begin{array}{c} 3 \\
1 \\
-1 \end{array} \right)
\end{eqnarray}\)
縦ベクトルの方が空間は計算しやすいのですが一応横でも書いておきます。
\(\overrightarrow{\mathrm{PS}}=(m-1\,,\,m-4\,,\,2)\)
\(\overrightarrow{\mathrm{PQ}}=(1\,,\,-2\,,\,0)\)
\(\overrightarrow{\mathrm{PR}}=(3\,,\,1\,,\,-1)\)
これらを使って
\(\hspace{10pt} \overrightarrow{\mathrm{PS}}=\alpha\, \overrightarrow{\mathrm{PQ}}+\beta \,\overrightarrow{\mathrm{PR}}\)
を座標で表します。
\(\begin{eqnarray} \left(\begin{array}{c} m-1 \\
m-4 \\
2 \end{array} \right)
&=&\alpha \left(\begin{array}{c} 1 \\
-2 \\
0 \end{array} \right)
+\beta \left(\begin{array}{c} 3 \\
1 \\
-1 \end{array} \right)\\
&=& \left(\begin{array}{c} \alpha+3\beta \\
-2\alpha+\beta \\
-\beta \end{array} \right)\end{eqnarray}\)
横ベクトルで表すと
\(\begin{eqnarray} (m-1\,,\,m-4\,,\,2)&=&\alpha (1\,,\,-2\,,\,0)+\beta (3\,,\,1\,,\,-1)\\
&=&(\alpha+3\beta\,,\,-2\alpha+\beta \,,\,-\beta )\end{eqnarray}\)
これらから \( m\) を求めます。
つまり
\( \begin{cases}
m-1= \alpha+3\beta\\ \\
m-4= -2\alpha+\beta \\ \\
\hspace{22pt} 2=-\beta \end{cases}\)
を解けば良いということです。
これを解くと、
\(\hspace{10pt}\displaystyle \alpha=\frac{7}{3} , \beta=-2 , \underline{ m=-\frac{8}{3} }\)
と答えが出ます。
これにより
\(\hspace{10pt} \mathrm{\overrightarrow{PS}=\displaystyle \frac{7}{3}\,\overrightarrow{PQ}-2\,\overrightarrow{PR}}\)
となり、
「同じ始点の、２つの独立なベクトルで表されている」
ので同一平面上にあると言えますね。
座標軸を入れて座標を確認してみるとわかりますか？
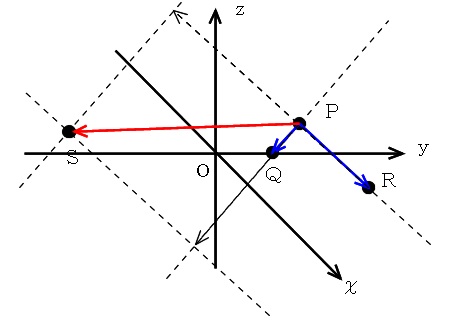座標はとらない方が分かり易いですね。
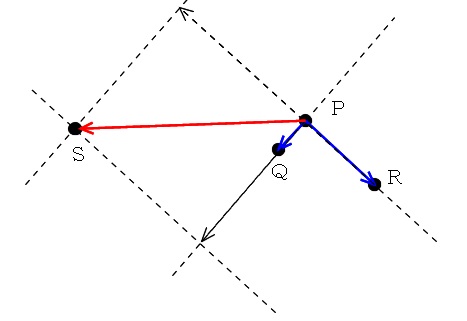
ベクトルで同一平面上、という条件で求めましたが、空間における「平面の方程式」を利用してみましょう。
知っているとかなり使えるので、時間が（余裕が）あれば見ておいて下さい。
平面の方程式を利用した解き方
\(\color{red}{\vec n=(a\,,\,b\,,\,c)} , \vec n\neq0\) を法線ベクトルとし、
点 \( \color{red}{\mathrm{A}(\,\alpha\,,\,\beta\,,\,\gamma\,)}\) を通る平面の方程式は、
\( \large{\color{red}{a(x-\alpha)+b(y-\beta)+c(z-\gamma)=0}}\)
となります。
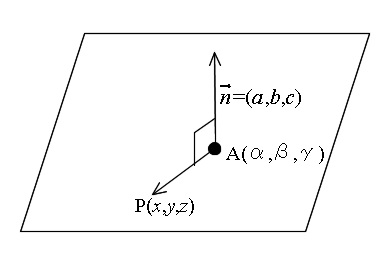
平面上の任意の点 \( \mathrm{P}(\,x\,,\,y\,,\,z\,)\) に対し、
\(\hspace{10pt}\overrightarrow {\mathrm{AP}}=(\,x-\alpha\,,\,y-\beta\,,\,z-\gamma\,)\)
であり、
法線ベクトル \(\vec n\) とは常に \( \overrightarrow {\mathrm{AP}}\cdot \vec n=0\) が成り立つので、
\(\hspace{10pt} a(x-\alpha)+b(y-\beta)+c(z-\gamma)=0\)
となります。
展開して定数項をまとめると、
\( \hspace{10pt}\large{\color{red}{ax+by+cz+d=0}}\)
とも書けます。
ただし、これを使うには法線ベクトルが必要になるので、
問題に与えあられている場合は良いのですが、
無い場合、ふつうの高校生の知識ではちょっと手間がかかる場合があります。
この問題はそれほどややこしくもありません。
平面が \(\mathrm{ P(1,3,2)\,,\,Q(2,1,2)\,,\,R(4,4,1)}\) の３点を通ることより、
法線ベクトル \(\vec n\) は \( \mathrm{\overrightarrow{PQ}\,,\,\overrightarrow{PR}}\) の両方に垂直です。
\(\begin{eqnarray} \overrightarrow{\mathrm{PQ}}&=&(1\,,\,-2\,,\,0)\\
\overrightarrow{\mathrm{PR}}&=&(3\,,\,1\,,\,-1)\\
\vec n&=&(a\,,\,b\,,\,c)
\end{eqnarray}\)
内積が\(\,0\,\)になることから、
\( \overrightarrow{\mathrm{PQ}} \cdot \vec n=a-2b=0\)
\( \overrightarrow{\mathrm{PR}} \cdot \vec n=3a+b-c=0\)
これらから \(a\,,\,c\) を \( b\) だけで表すと、
\( a=2b\,,\,c=7b\)
となるので、\(\vec n=(\,2b\,,\,b\,,\,7b\,)\)
ベクトルは実数倍しても方向は同じだから、
法線ベクトルの１つは \( (2\,,\,1\,,\,7)\) とすることができます。
すると３点 \(\mathrm{ P\,,\,Q\,,\,R}\) を通る平面の方程式は、点 \( \mathrm{P}\) を通ることより、
(点 \( \mathrm{R}\) でも点 \( \mathrm{Q}\) でも良いですよ。)
\(\hspace{10pt} 2(x-1)+(y-3)+7(z-2)=0\\ \\
\Leftrightarrow 2x+y+7z-19=0 ･･･①\)
平面①上に点 \( S\) があるので、\( (\,m\,,\,m-1\,,\,4\,)\) を代入して
\(\hspace{10pt} 2(m)+(m-1)+7(4)-19=0\\ \\
\Leftrightarrow \hspace{20pt} m=\underline{ -\displaystyle \frac{8}{3} }\)
実は、法線ベクトルの１つを求める簡単な方法があるのですが、直接目の前で作業しながら説明しないと使いきれない高校生が多いので、お互いの時間が無駄になる可能性が高いためここでは取り入れません。
法線ベクトルは1つではない
ただし、平面の方程式を求めるとき、（特に記述式の解答のとき）
法線ベクトルは \( (2\,,\,1\,,\,7)\) として良いのか？
と思うかもしれませんが、かまいません。
法線ベクトルは何倍しても方向性は変わらないし、\( (\,2b\,,\,b\,,\,7b\,)\) でも結果は同じになるので一般性は失われません。
解答上では
「法線ベクトルの１つは \( (\,2\,,\,1\,,\,7\,)\) なので、、、」
または
「法線ベクトルの１つは \( (\,2\,,\,1\,,\,7\,)\) と取れるので、、、」
としておけば減点対象にはならないはずです。
心配な人は \((\,2b\,,\,b\,,\,7b\,)\) や \((\,2k\,,\,k\,,\,7k\,)\) を法線ベクトルとしておくと良いです。
もちろん \(b\neq 0\) や \( k\neq 0\) を忘れずに書き足しておいてくださいね。
平面の方程式が使えると便利な問題を見ておきましょう。
もちろん、ベクトル（矢印ベクトル）で解ける問題でもあります。
空間ベクトルの要点は平面ベクトルと同時に見ておくことをおすすめしています。