三角形の形状決定問題と三角比と辺で表された等式の証明

三角形の形を問う問題を三角形形状決定問題といいます。
角と辺の関係が三角比で表されている条件から、それを変形して三角形の特徴的な条件を探し出すのです。
形状決定問題に入る前に三角比と辺の関係式を証明する問題も説明しておきます。

三角形の種類

三角形の形の名前を聞くなんて「中学生かよ！」
といわれそうですが、確認しておきます。

三角形の種類を聞かれて答えとなる三角形は、
　「二等辺三角形」「直角三角形」
がほとんどです。
「正三角形」は二等辺三角形でもありますので含めました。
もちろんこれだけではありません。

「\(\,\mathrm{∠A}\,\)が何度の\(\,△\,\)」というのも三角形の形状です。

「二等辺三角形」でもあり「直角三角形」でもある場合は
　「直角二等辺三角形」
と答えなければならないし、
直角三角形の場合はどこが直角なのかも示す必要があります。

もしかして、三角形の形状決定問題甘くみてました？
答え方だけで無く、根拠を述べることも簡単ではありません。

でも、安心してください！
方針は１つでおおよその問題が解決しますから。

三角形形状問題の解き方

三角形の形状決定問題がやっかいに見えるのは、
問題の関係式に、
　辺\(\,a\,,\,b\,,\,c\,\)と角\(\mathrm{\,A\,,\,B\,,\,C\,}\)が混ざっている
問題が多いからです。

だから方針は、
正弦定理
　\(\hspace{4pt} \displaystyle \color{red}{\frac{a}{\sin A}=\frac{b}{\sin B}= \frac{c}{\sin C}=2R}\)
余弦定理
　\(\begin{eqnarray}\displaystyle
\cos A&=&\frac{b^2+c^2-a^2}{2bc}\\
\cos B&=&\frac{c^2+a^2-b^2}{2ca}\\
\cos C&=&\frac{a^2+b^2-c^2}{2ab}
\end{eqnarray}\)
を使って、
「辺のみ」「角のみの関係」に統一することです。

「角のみの関係」というのは「三角比のみ」と考えてくださいね。

ただ、辺のみの関係式にする方が比率的には多いです。

角（三角比）と辺とで成り立つ等式の証明

形状決定の問題に行く前に準備運動しておきましょう。
関係式が成り立つことの証明問題です。

三角比の証明問題では、\(\sin\hspace{4pt}\)と\(\hspace{4pt}\cos\hspace{4pt}\)を辺に変えていくとうまくいくことが多いです。

三角比を辺に変えるにはどうすれば良いか？

正弦定理か余弦定理ですが、ここでは示す関係式に\(\,\cos A\,\)を残すので、
正弦定理を使って\(\,\sin\,\)を消しましょう。

正弦定理から
　\( \displaystyle \frac{a}{\sin A}=\frac{b}{\sin B}= \frac{c}{\sin C}=2R\)
なので
　\( \sin A=\displaystyle \frac{a}{2R}\,,\,\sin B=\displaystyle \frac{b}{2R}\,,\,\sin C=\displaystyle \frac{c}{2R}\)

ここは関係式が成り立つことを示すだけなのでサクッと済ませましょう。

外接円の半径は定数

\(\,R\,\)は外接円の半径で求まっていませんが、仮においても消えてくれます。

（１）\(\hspace{4pt}2b\cos A \sin B=\sin C\hspace{4pt}\)において、
　\(\hspace{4pt}\displaystyle \sin B=\frac{b}{2R}　,　\sin C=\frac{c}{2R}\)
を代入すると、
　\(\hspace{10pt}\displaystyle 2\cos A\cdot \frac{b}{2R}=\frac{c}{2R}\)

両辺に\(\,2R\,\)をかけると
　\(\hspace{10pt} 2b\cos A=c\)
と簡単に求める関係式を示すことができます。

（２）「\(\hspace{4pt}a\hspace{4pt}\)と\(\hspace{4pt}b\hspace{4pt}\)の関係」は両方『辺』です。

（１）から辺でない部分は\(\hspace{4pt}\cos A\hspace{4pt}\)だけです。

余弦定理ですね。

　\(\hspace{10pt} \cos A=\displaystyle \frac{b^2+c^2-a^2}{2bc}\)
を（１）の関係式に代入すると
　\(\begin{eqnarray} 2b\color{red}{\cos A}&=&C\\
2b\cdot \displaystyle \color{red}{\frac{b^2+c^2-a^2}{2bc}}&=&c\\
b^2&=&a^2
\end{eqnarray}\)

　\(a\hspace{4pt},\hspace{4pt}b\hspace{4pt}\)ともに辺なので正であるから、
　\(\hspace{10pt}\underline{　a=b　}\)

三角比の証明、三角形の形状を聞かれたら「辺の関係式に持ち込む」。
そのためにも、正弦定理、余弦定理は常に意識しておきましょう。

三角形の形状決定練習問題

ここからが本番です。

見えているのが\(\,\sin B\,\)や\(\,\sin C\,\)だけなので、
正弦定理を使うことは分かります。

正弦定理から
　\(\begin{eqnarray}
\color{red}{a}&=&\color{red}{2R\sin A}\\
\color{blue}{b}&=&\color{blue}{2R\sin B}\\
\color{magenta}{c}&=&\color{magenta}{2R\sin C}\end{eqnarray}\)
とおけるので
　\(\hspace{4pt} \color{blue}{b}+\color{magenta}{c}=2\color{red}{a}(\sin B+\sin C)\\
\Leftrightarrow \color{blue}{2R\sin B}+\color{magenta}{2R\sin C}=2\cdot \color{red}{2R\sin A}(\sin B+\sin C)\\
\Leftrightarrow 2R\sin B+2R\sin C-4R\sin A(\sin B+\sin C)=0\\
\Leftrightarrow 2R(\sin B+2\sin C)(1-2\sin A)=0\)

ここで
　\( R\neq 0 \,,\, \sin B+R\sin C\neq 0\)
（　\(\sin B\,,\,\sin C\,＞\,0\)　）
なので
　\(\hspace{10pt}1-2\sin A=0 \\
\displaystyle\Leftrightarrow \hspace{4pt} \sin A=\frac{1}{2}\\
\displaystyle\Leftrightarrow \hspace{4pt}A=30^\circ\,,\,A=150^\circ\)

よって\(\,\mathrm{△ABC}\,\)は
　\(\hspace{10pt}A=30^\circ\hspace{4pt}\)か\(\hspace{4pt}A=150^\circ\hspace{4pt}\)の三角形

この場合は角（三角比）に統一することで上手くいきました。

これを辺に統一すると、
　\( a=2R\sin A \Leftrightarrow \sin A=\displaystyle \frac{a}{2R}\)
　\( b=2R\sin B \Leftrightarrow \sin B=\displaystyle \frac{b}{2R}\)
　\( c=2R\sin C \Leftrightarrow \sin C=\displaystyle \frac{c}{2R}\)
から
　\(\hspace{10pt} b+c=2a(\sin B+\sin C)\\
\Leftrightarrow b+c=2a \left( \displaystyle \frac{b}{2R}+\displaystyle \frac{c}{2R} \right)\\
\Leftrightarrow b+c=a \left( \displaystyle \frac{b+c}{R} \right)\\
\Leftrightarrow a=R\)

となるので「なんだこれ？」となります。
※
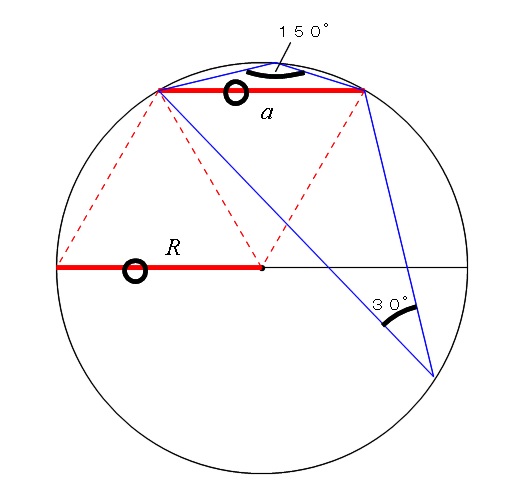
１辺\(\,a\,\)が外接円の半径\(\,R\,\)のとき、円周角は\(\,30°\,\)か\(\,150°\,\)になります。

普通は辺の関係に持ち込むと上手くいくのですが、
角度が具体的に出る三角形や直径を辺に持つ三角形では、
三角比のみの関係に持ち込む方が分かり易いのです。

これは見分けるというより、
実際に代入して見て、角だけがいいか、辺だけが良いかを判断した方がはやいです。

ただし、方程式で見れば正弦定理か余弦定理かはすぐに分かります。

　\(\color{red}{\sin}\,\)がある場合正弦定理で、
　\(\color{red}{\cos}\,\)がある場合余弦定理、
というだけです。

これは正弦定理と余弦定理の両方使うというのは分かりますよね？

正弦定理から
　\( \sin A=\displaystyle \frac{a}{2R}\)
　\( \sin B=\displaystyle \frac{b}{2R}\)
余弦定理から
　\( \cos C=\displaystyle \frac{a^2+b^2-c^2}{2ab}\)
と表されることから
　\(\hspace{10pt} 2\sin B \cos C=\sin A\\
\Leftrightarrow \hspace{4pt}2\cdot \displaystyle \frac{b}{2R}\cdot \displaystyle \frac{a^2+b^2-c^2}{2ab}=\displaystyle \frac{a}{2R}\\
\Leftrightarrow \hspace{4pt}\displaystyle \frac{b(a^2+b^2-c^2)}{2abR}=\displaystyle \frac{a}{2R}\\
\Leftrightarrow \hspace{4pt}\displaystyle \frac{a^2+b^2-c^2}{a}=a\\
\Leftrightarrow \hspace{4pt}a^2+b^2-c^2=a^2\\
\Leftrightarrow \hspace{4pt}b^2=c^2\)

ここで\(\,b\,,\,c\,＞\,0\,\)なので
　\(\hspace{10pt}b=c\)

よって\(\,\mathrm{△ABC}\,\)は、
　\(\hspace{10pt}\mathrm{AB=AC}\,\)の二等辺三角形　･･･（答）

どうです？
正弦定理、余弦定理を利用した後は、単なる等式処理ですよね。

図にたよることはできませんが、
「わからない」とあきらめる前に分かることだけでもやって見ましょう。

共通テストでも十分出出されそうですけどね。

⇒　正弦定理と余弦定理の使い方と面積の公式

正弦定理と余弦定理は必ず使うことになります。

⇒　三角比（図形と計量）の要点

センター試験で三角形の形状問題を見かけませんでした。
共通テストではどうでしょう。三角比は必須問題です。