円に内接する四角形の面積は特殊な条件のもとでは直接つかえる公式もありますが必要ありません。
三角比の定理だけで簡単に解決できますので基本的な定理を利用することから始めてください。
円に内接するといろいろな条件がそろうので使える定理も増えますよ。
円に内接する四角形の図の書き方
「円に内接する四角形の書き方?何でそんなことから?」
と思うかもしれませんが、これが図形問題をとくときの始まりなのです。
いくら定理や裏技みたいな公式を覚えようが、
この作業をしない人は数学の成績はあがりませんよ。
問題を見て図を書いてみましょう。
円に内接する4角形\(\,\mathrm{ABCD}\,\)があり、
\(\hspace{4pt}\mathrm{AB}=4\hspace{4pt},\hspace{4pt}\mathrm{BC}=3\hspace{4pt},\hspace{4pt}\mathrm{DC}=5\hspace{4pt},\hspace{4pt}\mathrm{DA}=6\)
とするとき、次の問いに答えよ。
(1)\(\sin \angle {\mathrm{BAD}}\,\)の値を求めよ。
(2)4角形\(\,\mathrm{ABCD}\,\)の面積を求めよ。
何度もいっていることですが、
この問題のように文章だけで図がない問題(センターは明らかにわざとです。笑)では、
図を書くことから始まります。
出来るだけ正確な図が望ましいのですが、
定規が持ち込めない試験においては限度がありますので「出来るだけ正確に」です。
ただし、こだわると時間が足りなくなるかもしれませんので、ほどよく「適当に」で良いですよ。
「円に内接する四角形」を書くときは、
円を先に書くか?四角形を先に書くか?
円を先に書くと書きやすいような気がしますが好きにしてください。
円を先に書く場合は、直径を二等分するとある程度「中心の位置が分かる」ので使えます。
しかし、後から書く方法もあるのでどちらでも自分が書きやすい方で良いです。
問題にある条件通りに図を書いてみることにしましょう。
ここでは円を先に書きます。
円があって、
\(\hspace{4pt} \mathrm{AB=4\,,\,BC=3\,,\,DC=5\,,\,DA=6}\)
から
\(\hspace{4pt}\mathrm{BC\,<\,AB\,<\,DC\,<\,DA}\)
となるように頂点を探していきます。
(\(\,\mathrm{AD}\,\)と\(\,\mathrm{BC}\,\)を平行にすると等脚台形になり、
\(\,\mathrm{AB=DC}\,\)となるので少し傾けると良いです。)
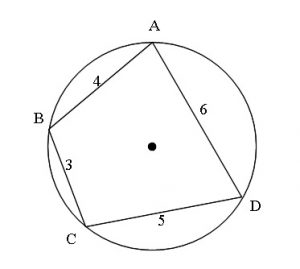
おおよそでしか書けないのでだいたいで良いのですが、
出来る限り問題の条件通りに書いた方が、後々解法への方針が見通しやすいです。
図を見ていると対角線を引きたくなりますがちょっと我慢します。
え?
「対角線」引きたくなりませんか?
三角形がたくさんできるのでいろいろなことが分かりそうでしょう?
三角比の定理って三角形においての定理ばかりですよ。
三角形についての角と辺との関係を三角比というくらいですからね。
正弦定理か余弦定理の選択
(1)問題は
「\(\hspace{4pt}\sin \angle {\mathrm{BAD}}\hspace{4pt}\)の値を求めよ。」
です。
\(\hspace{4pt}\sin \angle {\mathrm{BAD}}\hspace{4pt}\)を求めるので、
『正弦定理』?
と思うかもしれませんが外接円の半径は分かっていません。
そこで\(\hspace{4pt}\sin \angle {\mathrm{BAD}}\hspace{4pt}\)を求めるのだから、
\(\hspace{4pt}\sin^2 \theta+\cos^2 \theta=1\hspace{4pt}\)
という三角比の相互関係を利用すれば、
\(\color{red}{\cos \angle {\mathrm{BAD}}}\hspace{4pt}\)から求めれば良いので、
『余弦定理』と方針変更です。
三角比と図形の融合は普通ですが、
『正弦定理』と『余弦定理』
は常に引き出しに入れておくのは当然ですね。
補角の公式の利用
対角線\(\,\mathrm{BD}\,\)を補助線として入れて余弦定理を使うというのは分かると思います。
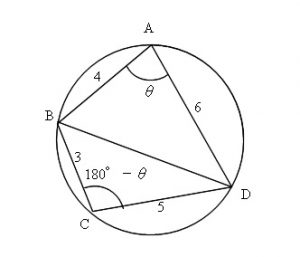
しかし、内接四角形の場合
「内対角の和が\(\,180\,\)度」
なので、
\( \angle \mathrm{C}+\angle \mathrm{A}=180^\circ \hspace{7pt} \Leftrightarrow \hspace{7pt} \angle \mathrm{C}=180^\circ-\angle \mathrm{A}\)
この場合、対角の\(\hspace{4pt}\sin\hspace{4pt}\)や\(\hspace{4pt}\cos\hspace{4pt}\)において
\(\hspace{10pt}\color{red}{\sin \mathrm{A}=\sin \mathrm{C}}\)
であり、
\(\hspace{10pt}\color{red}{\cos \mathrm{A}=-\cos \mathrm{C}}\)
である、ということを忘れがちです。
しっかり記憶しておいてください。
\(\hspace{10pt}\color{blue}{\sin (\,180^\circ-\theta\,)=\sin \theta}\)
\(\hspace{10pt}\color{blue}{\cos (\,180^\circ-\theta\,)=-\cos \theta}\)
ですからね。

\(\,\mathrm{△ABD}\,\)と\(\,\mathrm{△CBD}\,\)に余弦定理を用いると、
\( \mathrm{\color{magenta}{BD^2}=\color{red}{AB^2+AD^2-2AB\cdot AD\cos \angle{BAD}}}\)
\( \mathrm{\color{magenta}{BD^2}=\color{blue}{CB^2+DC^2-2CB\cdot DC\cos \angle{BCD}}}\)
これらを連立して
\(\hspace{10pt} \color{red}{\mathrm{AB^2+AD^2-2AB\cdot AD\cos \angle{BAD}}}\\
=\color{blue}{\mathrm{CB^2+DC^2-2CB\cdot DC\cos \angle{BCD}}}\)
ここで
\( \mathrm{\cos \angle{BCD}=-\cos \angle{BAD}}\)
なので\(\hspace{4pt}\mathrm{\angle BAD}=\theta\hspace{4pt}\)とおくと
\(\hspace{10pt} \mathrm{4^2+6^2-2\cdot 4\cdot 6\cdot \cos \theta\\
=3^2+5^2-2\cdot 3\cdot 5\cdot (-\cos \theta)}\\
\Leftrightarrow \hspace{7pt} 52-48\cos \theta=34+30\cos \theta\)
より
\( \cos \theta=\cos \mathrm{\angle BAD}=\displaystyle \frac{3}{13}\)
また
\(\begin{eqnarray}
\sin^2 \theta+\cos^2 \theta&=&1\\
\sin^2\theta&=&1-\cos^2\theta\\
&=&1-\left(\frac{3}{13}\right)^2\\
&=&\frac{160}{169}
\end{eqnarray}\)
および\(\hspace{4pt} \sin \theta \,>\,0\hspace{4pt}\)であることから
\(\hspace{10pt} \mathrm{\sin \angle BAD}=\underline{ \displaystyle \frac{4\sqrt{10}}{13} }\)
これは、\(\mathrm{\sin \angle BCD}\,\)でもあります。
正弦定理か余弦定理かのどちらかを選ぶ基準はおおよそ決めていて良いです。
この問題のケースも余弦定理ですよね。
四角形の面積の求め方
普通だと四角形の面積が公式で求められるのは
「平行四辺形」(正方形、長方形、ひし形も平行四辺形です。)
と「台形」くらいでしょう。
だから、どのような四角形の面積でも求められる方法が必要です。
(2)「4角形\(\,\mathrm{ABCD}\,\)の面積を求めよ。」
(1)ができれば面積は簡単です。

\(\hspace{4pt}四角形\mathrm{ABCD=△ABD+△CBD}\,\)
より、 四角形\(\,\mathrm{ABCD}\,\)の面積を\(\,\mathrm{S}\,\)とすると
\(\begin{eqnarray}\displaystyle
\mathrm{S}&=&\mathrm {\triangle{ABD}+\triangle{CBD}}\\
&=&\mathrm{ \frac{1}{2}\cdot 4\cdot 6\cdot \sin \angle{BAD}+\frac{1}{2}\cdot 3\cdot 5\cdot \sin \angle{BCD}}\\
&=&\frac{1}{2}\cdot 4\cdot 6\cdot \frac{4\sqrt{10}}{13}+\frac{1}{2}\cdot 3\cdot 5\cdot \frac{4\sqrt{10}}{13}\\
&=&\underline { 6\sqrt{10} }\end{eqnarray}\)
計算結果は自分で確かめないと意味ありませんよ。
分母の\(\,\color{red}{13}\,\)がきれいに消えているのはどこの段階なのか分かりますか?
このように四角形の面積は三角形2つに分けて、加えるというのが多いです。
「角の二等分線」で切られる三角形も同じ角を持つので良く問題に組み込まれますね。
大切なのは図を書いて同じ角度だということを目で確認することです。
特別な場合に使える四角形の面積の公式
「内接四角形で4辺が分かっている場合」の面積には公式があります。
円に内接している四角形の4辺が\(\hspace{4pt} a\,,\,b\,,\,c\,,\,d\hspace{4pt}\)で
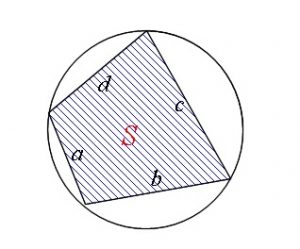
\(\hspace{4pt}2s=a+b+c+d\)
としたとき、内接四角形の面積を\(\,S\,\)とすると
\(\hspace{10pt}\displaystyle \color{red}{S=\sqrt{(s-a)(s-b)(s-c)(s-d)}}\)
という公式があります。
当会の『覚え太郎』を使っている人は中学生でも知っていると思います。
名前は覚えなくて良いですが、
計算がややこしくなりすぎる場合があるので、
\(\hspace{4pt} 2s\hspace{4pt}\)が偶数の場合の使用にとどめておいた方が良いです。
この問題では、
\(\hspace{10pt} 2s=3+4+5+6=18\)
から
\(\hspace{10pt} s=9\)
よって、
\(\begin{eqnarray}\displaystyle
S&=&\sqrt{(9-3)(9-4)(9-5)(9-6)}\\
&=&\sqrt{6\cdot 5\cdot 4\cdot 3}\\
&=&\underline{ 6\sqrt{10} }
\end{eqnarray}\)
と出すことも出来ます。
割と\(\,4\,\)辺の和が偶数である問題は多いですが、
こればっかりにたよっていると、
応用範囲が広い前半の方法が使えなくなるので気をつけてください。
正弦定理を使う場合もあります。
使い分けはできるようになっておきましょう。
直接使う問題は少ないですが、余弦定理には\(\,2\,\)種類あるということも確認しておきましょう。