集合で記号と用語の意味のまとめです。
集合で使う記号には意味があり、データの活用と同じように知らなければ使えない、問題が解けないものが多くあります。
要素と部分集合や真部分集合の使い分け、和集合や補集合の意味を先ずは覚えましょう。
ド・モルガンの法則は覚えなくても通用しますので基本的な考え方をマスターして下さい。
「用語が先」といつも言っているのでここはやる予定はなかったのですが、具体例を挙げて高校の集合で使う用語の説明します。
ド・モルガンの法則については形を覚えるよりもっと良い方法がありますので見ておいてください。
集合と要素と記号
例えば、
「6の正の約数の全体」
のようにある条件を満たすもの全体の集まりを「集合」といいます。
また、集合を構成している1つひとつのものを集合の「要素」といいます。
集合を表すとき、\( A\hspace{4pt}\)などの文字を使いますが内容(要素)を示したいときは、
要素をならべて\(\hspace{4pt}\{a,b,c\}\hspace{4pt}\)のようにカッコでくくって表します。
6の正の約数全体:\(\hspace{4pt}\{1,2,3,6\}\)
これを
{\(\hspace{4pt} x\hspace{4pt}\)|\(\hspace{4pt}x\hspace{4pt}\)は6の正の約数}
と表すこともできます。
他にも\(\hspace{4pt} x^2\,<\,100\hspace{4pt}\)を満たす正の整数の集合は、
{\(\hspace{4pt}x\hspace{4pt}\)|\(\hspace{4pt} x^2\,<\,100\hspace{4pt},\hspace{4pt}x\hspace{4pt}\)は正の整数}
のように文字を使って条件を示すことで集合を表すこともあります。
問題によって書き方が違う場合がありますので、
どちらも同じ意味であることを知っておいてください。
1つの要素\(\hspace{4pt}a\hspace{4pt}\)について、集合\(\hspace{4pt}A\hspace{4pt}\)の要素であることを
\(\hspace{10pt} \color{red}{a\,\in \,A}\) ・・・①
と表します。
「\(\hspace{4pt}a\hspace{4pt}\)は\(\hspace{4pt}A\hspace{4pt}\)の要素である。」
と読めば良いです。
※(注意)
\( A \ni a\) と書くこともできますがやめておいてください。
何故かなど気にせず、大学に進んでからにしておく方が無難です。
\(\hspace{4pt} a\hspace{4pt}\)が\(\hspace{4pt}A\hspace{4pt}\)の要素ではないとき、
\(\hspace{4pt} \color{red}{a\,\notin \,A}\)
と書き、①の否定を表します。
また、方程式などで使う『=』ですが、
集合の場合、「すべての要素が一致するとき」と定義されます。
{\(x\hspace{4pt}\)|\(\hspace{4pt}x\hspace{4pt}\)は6の正の約数}=\(\,\{\,1,2,3,6\,\}\,\)
記号を用いてまとめると
2つの集合\(\,A\,,\,B\,\)において\(\,A=B\,\)であるとは、
\(\hspace{10pt} x \in A \hspace{4pt} \Leftrightarrow \hspace{4pt}x \in B\)
が成り立つことです。
簡単にいえば、
\( A\,\)の要素をとればそれは必ず\(\,B\,\)の要素であり、
\( B\,\)の要素をとればそれは必ず\(\,A\,\)の要素である。
ということです。
1つでもはずれればダメです。
有限集合と無限集合
「6の正の約数全体」\(\hspace{4pt} \{\,1,2,3,6\,\}\)
のように数に限りがある集合を「有限集合」といい、
「正の奇数の個数全体」 \( \{\,1,3,5,7,\cdots\}\)
のように限りがない集合を「無限集合」といいます。
高校であつかう整数の集合は「有限集合」だけだと思っていて良いです。
(実数の範囲で不等式を満たす集合は「無限集合」です。)
ただ、要素を1つも含まない集合を「空集合」(くうしゅうごう)といいますので注意が必要です。
例えば、
「\(\hspace{4pt}x^2=-1\hspace{4pt}\)を持たす実数\(\hspace{4pt}x\hspace{4pt}\)の集合」
には要素がありませんので空集合となります。
空集合を表す記号は\(\hspace{4pt}\phi\hspace{4pt}\)です。
これには注意が必要で、\(\hspace{4pt}\phi\hspace{4pt}\)は集合を表しているのであって、要素を表しているのではありません。
だから \( \color{red}{\{} \hspace{4pt}\phi\hspace{4pt} \color{red}{\}}\hspace{4pt}\)とはしません。
部分集合と真部分集合
2つの集合\( \,A\,,\,B\,\)があって、
集合\(\,B\,\)の要素のどれを取り上げても、
それが、集合\(\,A\,\)の要素であるとき、
「集合\(\,B\,\)は集合\(\,A\,\)の『部分集合』である。」
といいます。
記号で表すと
\(\hspace{10pt} B \subseteq A \)
または
\(\hspace{10pt} A \supseteq B \)
と表します。
要素を表すときは \( a\in A \) (左に要素)だけを使うように注意しましたので、集合のときも \( B\subset A \) のように限って使うようにしておくと間違えなくて済みます。
問題にあるときは読み取れればそれで良いです。
また、
\(\hspace{10pt} B \subseteq A\)
であり、かつ\(\hspace{4pt} B\neq A\hspace{4pt}\)が分かっているとき、
「\(\hspace{4pt}B\hspace{4pt}\)は\(\hspace{4pt}A\hspace{4pt}\)の『真部分集合』である。」
といいます。
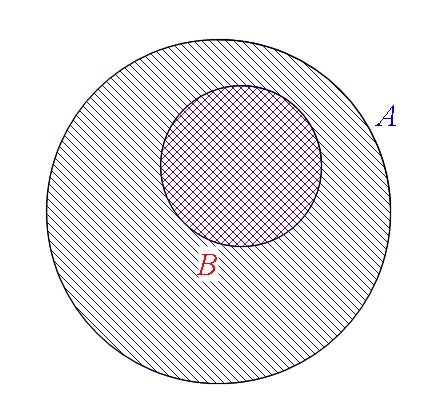
記号では
\( B \subset A\) や \( A \supset B\)
と書き表します。
分かりにくいですけど、\(\,B\,\)の要素は\(\,A\,\)に含まれているけど、
完全に一致はしていない(\(\,A\,\)の要素は他にもある)ということですね。
※特に注意
「\(\hspace{4pt}\in\hspace{4pt}\)」は要素を表し、
「\(\hspace{4pt}\subseteq\hspace{4pt}\)」や「\(\hspace{4pt}\subset\hspace{4pt}\)」は集合を表している、
ということは忘れないでください。
教科書にあるこの記号の意味を知らない、というか忘れている高校生が多いです。
(現行の教科書では部分集合を\(\hspace{4pt}\subset\hspace{4pt}\)だけで表しますので、
真部分集合と部分集合の使い分けは必要無いようですので知らなくて普通ですね。)
\( a\in A\hspace{4pt}\)は\(\hspace{4pt}\{a\} \subset A\hspace{4pt}\)と書いても間違いではありません。
しかし、
\( a\in A\hspace{4pt}\)を\(\hspace{4pt} a \subset A\hspace{4pt}\)と書くことはできません。
要素と集合の違いは覚えておきましょう。
空集合\(\hspace{4pt}\phi\hspace{4pt}\)は任意の集合の部分集合と約束しますので、
\(A\,\)を任意の集合とすると\(\hspace{4pt}\phi \subset A\hspace{4pt}\)です。
ここまでの確認問題です。
集合\(\hspace{4pt}A\hspace{4pt}\)の要素が\(\hspace{4pt} a,b,c\hspace{4pt}\)の3つのとき、\( A\,\)の部分集合を全て書き出せ。
答えだけでいいでしょう。
\(\hspace{10pt} \{a\}\,,\,\{b\}\,,\,\{c\}\,,\\
\hspace{4pt}\,\{a,b\}\,,\,\{b,c\}\,,\,\{c,a\}\,,\\
\hspace{4pt}\,\{a,b,c\}\,,\,\phi\)
の8個となります。
要素が5個になると部分集合は\(\hspace{4pt} 2^5=32\hspace{4pt}\)個になります。
要素が10個になると\(\hspace{4pt} 2^{10}=1024\hspace{4pt}\)個になります。
これは要素1つひとつに対し、
部分集合に入れるか入れないかでふた通りの選択
ができるからです。
ここは用語の確認だけのはずが、横道にそれました。
元に戻します。
共通部分と和集合と補集合
集合における「かつ」や「または」や「否定」の用語です。
共通部分(共通集合、積集合、交わり)
2つの集合\(\,A\,,\,B\,\)に共通な要素全体からなる集合を、
\(\,A\,,\,B\,\)の「共通部分」といいます。
\( A\,\)と\(\,B\,\)の共通部分は\(\hspace{4pt} \color{blue}{A \cap B}\hspace{4pt}\)と表します。
( \( A \cap B\hspace{4pt}\)は「\(\,A\,\)キャップ\(\,B\,\)」と読んでいいです。)
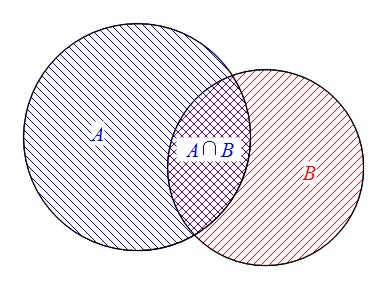
別の表し方をすると、
\( A \cap B=\{\hspace{4pt}x\hspace{4pt}|\hspace{4pt}x\in A\hspace{4pt}\color{red}{かつ}\hspace{4pt}x\in B\hspace{4pt}\}\)
です。
この「共通部分」は、「共通集合」や「積集合」や「交わり」ともいいます。
\( A,B\,\)が共通要素を持っていないとき、\( A,B\,\)は「互いに素である」といいます。
つまり、
\( A \cap B= \phi\hspace{4pt}\)のとき「互いに素」ということです。
和集合(合併集合、結び)
2つの集合\(\,A\,,\,B\,\)の要素をすべて合わせて得られる集合を、
\(A\,,\,B\,\)の「和集合」
といいます。
\(A\,\)と\(\,B\,\)の和集合は\(\hspace{4pt} \color{red}{A \cup B}\hspace{4pt}\)と表します。
( \( A \cup B\hspace{4pt}\)は「\(\,A\,\)カップ\(\,B\,\)」と読んで良いです。 )

別の表し方をすると、
\( A \cup B=\{\hspace{4pt}x\hspace{4pt}|\hspace{4pt}x\in A\hspace{4pt}\color{red}{または}\hspace{4pt}x\in B\hspace{4pt}\}\)
です。
この「和集合」は、「合併集合」や「結び」ともいいます。
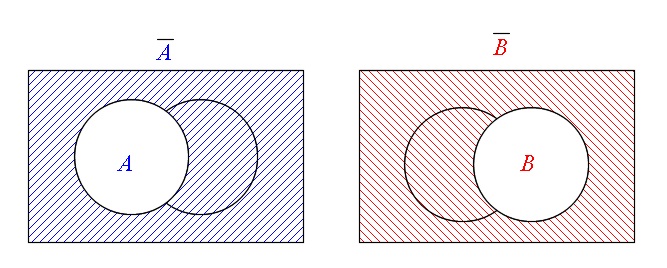
補集合
1つの全体集合を\(\hspace{4pt}U\hspace{4pt}\)として、\(\hspace{4pt}U\hspace{4pt}\)の部分集合\(\hspace{4pt}A\hspace{4pt}\)について考えるとき、
\( A\hspace{4pt}\)に属さない\(\hspace{4pt}U\hspace{4pt}\)の要素全体からなる集合のことを
\(A\hspace{4pt}\)の『補集合』
といいます。
簡単にいうと、\(U\hspace{4pt}\)の中で\(\hspace{4pt}A\hspace{4pt}\)ではない集合のことです。
\( A\hspace{4pt}\)の補集合は\(\hspace{4pt}\overline{A}\hspace{4pt}\)と表します。

関係を要素で表すと
\(\hspace{10pt}x \in \overline{A} \hspace{10pt} \Leftrightarrow \hspace{10pt} x\notin A\)
集合で表すと
\( A\cap \overline{A}=\phi\)
\( A\cup \overline{A}=U\)
が成り立ちます。
ド・モルガンの法則とベン図の利用
補集合に関して次の等式が成り立ちます。
\(\hspace{10pt}\large{ \color{red}{\overline{A\cup B}=\overline A \cap \overline B}}\)
\(\hspace{10pt} \large{\color{red}{\overline{A\cap B}=\overline A \cup \overline B}}\)
これを『ド・モルガンの法則』といいます。
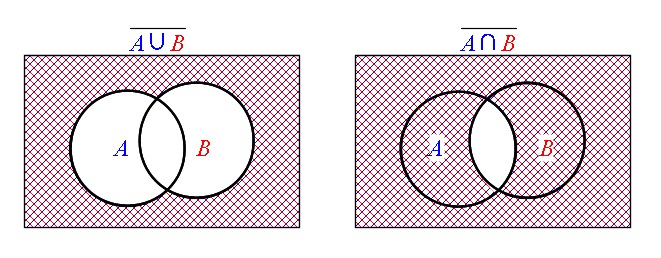
覚えられない人は覚えなくて良いですが、ベン図で確認はできるようになってください。
書けば良いだけですよ。
用語はこれくらいです。
考えても出てこないものなので意味さえ知らない、というのは通用しません。
覚えておいてください。
ちょっとした補足
ド・モルガンの法則を覚えていなくてもベン図で解けるというのが分かります。
数と式のまとめですがもう一度基本用語を確認できます。