高校の数学Ⅰの始まり数と式の要点です。
整式の計算、因数分解、2重根号を含む実数、絶対値と不等式、集合と命題といった数学の基礎用語がたくさんあります。
数学Ⅰでは他の分野にも必要な用語や公式がたくさんあるので必ず仕上げておきましょう。
数と式の項目
教科書では「数と式」という単元になっていますが、数学はすべて数と式で成り立っているようなものです。
言語なので、いろいろな表現を持っていますが数や大きさや関係の記号を変えているだけです。
この単元では「式の計算」「実数」「1次不等式」「集合と命題」という項目で取り上げますが、
すべてに共通して言えることなのでここで学ぶことは当たり前と言えるようになっておきましょう。
その後は記号や意味が表し方を変えて出てくるだけです。
式と計算
中学でも多少は済ませてありますが数と文字式の計算です。
整式の加法と減法
整式の足し算引き算です。
整式とは多項式のことですが、中学の復習を兼ねてまとめておきます。
単項式と多項式
数と文字の積(掛け算)だけで作られる1つ式を単項式といい、
単項式において文字の前に書く約束としてある数字をその単項式の係数といいます。
また掛けられている文字の数を次数といいます。
例えば、
\(\hspace{10pt}5\,,\,x\,,\,4x^2y\,\)
は単項式で、
係数はそれぞれ\(\,5\,,\,1\,,\,4\,\)
次数はそれぞれ\(\,0\,次\,,\,1\,次\,,\,3\,次\,\)
となります。
※
定数の\(\,5\,\)は\(\,0\,\)次の項の係数とみることができます。
係数の\(\,1\,\)と次数の\(\,1\,\)は普通は省略します。
単項式の和として表された式を多項式、または整式といい、
一つひとつ単項式を項といいます。
多項式\(\hspace{10pt}3x^2-4x+5\)
の項は\(\,3x^2\,,\,-4x\,,\,+5\,\)となります。
整式の中で文字の次数が同じである項を同類項といいます。
ただし、文字が\(\,2\,\)種類以上ある場合、すべての文字の次数が同じであるものです。
例えば、\(\,6x^2y^2\,\)と\(\,7x^2y^3\,\)は\(\,y\,\)の次数が違うので同類項とはいいません。
※
特定の文字を変数とみて次数を見るときは、他の文字は定数と見なします。
そのため\(\,x\,\)の整式とみた場合は\(\,6x^2y^2\,\)と\(\,7y^3x^2\,\)が同類項となります。
多項式において最も次数の高い項の次数をその整式の次数といいます。
例えば、\(\,5+2x^3+5x\,\)の次数は\(\,3\,\)次です。
ここまでの用語で整式を定義しておきます。
\(\color{red}{\fbox{ 整式の定義 }}\)
\(a_0\,,\,a_1\,,\,a_2\,,\,\cdots\,,\,a_n\)
が変数\(\,x\,\)によらない定数とするとき整理すると
\(\,P(x)=a_0\,x^n+a_1\,x^{n-1}+\cdots +a_{n-1}x+a_n\,\)
と表せる式を\(\,x\,\)の整式という。
このとき、
\(\,a_0\,\)≠\(\,0\,\)ならば\(\,P(x)\,\)は\(\,n\,\)次の整式という。
変数\(\,x\,\)を含まない項を定数項といいます。
降べきの順と昇べきの順
整式を次数の高い項の順に並べることを降べきの順に整理するといい、
\(\hspace{10pt}x^3+2x^2+3x+4\)
逆に、次数の低い順に整理することを昇べきの順に整理するといいます。
\(\hspace{10pt}4+3x+2x^2+x^3\)
整式の加法と減法
整式の足し算と引き算です。
整式\(\,\mathrm{A}\,\)と\(\,\mathrm{B}\,\)の和は\(\,\mathrm{A+B}\,\)
整式\(\,\mathrm{A}\,\)と\(\,\mathrm{B}\,\)の差は\(\,\mathrm{A+(-B)=A-B}\,\)
のように数の計算と同じように計算できますが、同類項をまとめるのが原則です。
\(\hspace{10pt}(2x^2+3x-1)-(4x^2-5x-6)\\
=2x^2+3x-1-4x^2+5x+6\\
=-2x^2+8x+5\)
整式の乗法
整式の掛け算です。
数でも文字式でも同じことは言えますので、計算法則を確認しておきます。
指数法則と分配法則
\(\,a^n\,\)は\(\,a\,\)を\(\,n\,\)回掛けたもので\(\,a\,\)の\(\,n\,\)乗と呼びます。
\(\,a\,\)を底、\(\,n\,\)を指数といいます。
※
「底」の内容は数学\(\,\mathrm{Ⅱ}\,\)で学びますが名前だけでも覚えておきましょう。
\(\color{red}{\fbox{ 指数法則 }}\)
\(\,m\,,\,n\,\)を正の整数とすると、
\(\hspace{10pt}a^m\times a^n=a^{m+n}\)
\(\hspace{10pt}(a^m)^n=a^{mn}\)
\(\hspace{10pt}(ab)^n=a^n\,b^n\)
が成り立つ。
例えば、
\(\hspace{10pt}x^3\times x^4=x^{3+4}=x^7\)
\(\begin{eqnarray}(\,2\,x^2\,y^3\,)^3&=&2^3\cdot (x^2)^3\cdot (y^3)^3\\
&=&8\,x^6\,y^9\end{eqnarray}\)
数学\(\,\mathrm{Ⅱ}\,\)で指数関数を学んだ後なら、
指数は整数から実数に拡張できることが分かります。
\(\color{red}{\fbox{ 分解法則 }}\)
整式\(\,A,B,C\,\)において
\(\hspace{10pt}A(B+C)=AB+AC\)
\(\hspace{10pt}(A+B)C=AC+BC\)
これは今までも普通に計算してきたことです。
例えば、次の式を展開すると
\(\begin{eqnarray}(a+b)(c+d)&=&a(c+d)+b(c+d)\\
&=&ac+ad+bc+bd\end{eqnarray}\)
となることをまとめているだけです。
展開公式
展開公式は中学からの引き継ぎになります。
\(\color{red}{\fbox{ 展開の公式 }}\)
\(\hspace{10pt}(a+b)^2=a^2+2ab+b^2\)
\(\hspace{10pt}(a-b)^2=a^2-2ab+b^2\)
\(\hspace{10pt}(a+b)(a-b)=a^2-b^2\)
\(\hspace{10pt}(x+a)(x+b)=x^2+(a+b)x+ab\)
\(\hspace{10pt}(ax+b)(cx+d)=acx^2+(ad+bc)x+bd\)
\(\hspace{10pt}(a+b+c)^2=a^2+b^2+c^2+2ab+2bc+2ca\)
展開は地道に計算すれば答えは出ますが、覚えていた方が結果は早く出ます。
\(\,4\,\)番目は逆の計算になる因数分解で「タスキガケ因数分解」として覚えることになるので覚えなくても良いです。
\(\,4\,\)番目の展開においては暗算する方が時間がかかるので地道に展開した方が確実で早いですよ。
\(\,5\,\)番目の公式は因数分解で利用するし、
展開したときの項が多くなるので計算時間短縮のためにも覚えておきましょう。
といっても、
どの単元でも出てくるような計算公式なので、
普通に練習問題を繰り返せばすべての公式は覚えることにはなります。笑
整式の除法は、何故か数学\(\,\mathrm{Ⅱ}\,\)になっています。
なので整式をまとめて理解するには、余裕があればですけど数学\(\,\mathrm{Ⅱ}\,\)まで一気に進めた方が良いですね。
または、数学\(\,\mathrm{Ⅱ}\,\)で除法を学んだ後もう一度数学\(\,\mathrm{Ⅰ}\,\)を見直すかです。
因数分解
因数分解とは与えられた整式を約数の積にすることです。
計算としては展開の逆ですね。
一応因数分解の公式をあげておきます。
\(\color{red}{\fbox{ 因数分解の公式 }}\)
\(\hspace{10pt}a^2+2ab+b^2=(a+b)^2\)
\(\hspace{10pt}a^2-2ab+b^2=(a-b)^2\)
\(\hspace{10pt}a^2-b^2=(a+b)(a-b)\)
\(\hspace{10pt}x^2+(a+b)x+ab=(x+a)(x+b)\)
\(\hspace{10pt}acx^2+(ad+bc)x+bd=(ax+b)(cx+d)\)
\(\hspace{10pt}a^2+b^2+c^2+2ab+2bc+2ca=(a+b+c)^2\)
\(\,5\,\)番目の因数分解はタスキガケ因数分解ですので、
形で覚えるのでは無くて実際に係数を与えて練習した方が早いです。
対称式と交代式
整式の因数分解と同時にやっておいた方が良いのは対称式と交代式です。
教科書の項目には特に取り上げて無いかもしれませんが、非常に大切な項目ですよ。
余裕がある人は見ておいてください。
\(\color{red}{\fbox{ 対称式 }}\)
2つの文字\(\,x,y\,\)の整式において\(\,x,y\,\)を入れかえても、
元の整式と同じになるものを対称式といいます。
例:\(\hspace{10pt}x^3+y^3\,,\,x^2+y^2-x-y\)
対称式は\(\,x+y\,,\,xy\,\)の基本対称式を用いて表すと便利なことが多いです。
例えば、
\(\hspace{10pt}x^2+y^2=(x+y)^2-2xy\)
\(\hspace{10pt}x^3+y^3=(x+y)^3-3xy(x+y)\)
という変形です。
\(\color{red}{\fbox{ 交代式 }}\)
2つの文字\(\,x,y\,\)の整式において\(\,x,y\,\)を入れかえると、
元の整式と符号が逆になるものを交代式といいます。
例えば、
\(\hspace{10pt}x^3-y^3\)
において\(\,x,y\,\)を入れかえると
\(\hspace{10pt}y^3-x^3=-(x^3-y^3)\)
のように符号が逆になります。
交代式は\(\,x+y\,,\,xy\,\)に加え\(\,x-y\,\)を使って変形すると便利です。
\(\hspace{10pt}x^3-y^3=(x-y)^3+3xy(x-y)\)
もちろん因数分解もよく利用するので
\(\hspace{10pt}x^3-y^3=(x-y)(x^2+xy+y^2)\)
と同時に覚えておくと良いです。
文字が3つの場合の対称式についても同じことが言えますが、
基本対称式が少し違ってきます。
対称式変形はいろいろな分野での求値問題でよく出てくるので使える様になっておくと良いです。
3次式の展開と因数分解
3次式が発展になっている教科書もありますが、普通の公式です。
\(\hspace{10pt}\color{red}{(a+b)^3=a^3+3a^2b+3ab^2+y^3}\)
\(\hspace{10pt}\color{red}{(a-b)^3=a^3-3a^2b+3ab^2-y^3}\)
\(\hspace{10pt}\color{red}{(a+b)(a^2-ab+b^2)=a^3+b^3}\)
\(\hspace{10pt}\color{red}{(a-b)(a^2+ab+b^2)=a^3-b^3}\)
逆の計算が因数分解になります。
1つ証明しにくい公式をあげておきます。
\(\hspace{10pt}\color{blue}{a^3+b^3+c^3-3abc}\\
=\color{blue}{(a+b+c)(a^2+b^2+c^2-ab-bc-ca)}\)
証明を上のリンク先「因数分解公式一覧」ページで示してありますが、
証明は公式を覚えて使える様になってからで良いです。
オイラーの分数式は、良い因数分解の練習になります。
実数
自然数、整数、有理数、無理数までの数を実数といいます。
無理数は中学でも扱っているので説明し直すまでもないでしょう。
線分の長さを表せる数が正の実数です。
それに符号を変えた数と、\(\,0\,\)を加えれば実数全体になります。
実数の分類
自然数や整数は説明するまでもないでしょう。
有理数は、整数、有限小数、無限小数に分けることができます。
簡単に言えば\(\,\displaystyle \frac{\,整数\,}{\,整数\,}\,\)で表せる数のことです。
無限小数の中で循環しない無限小数を無理数といいます。
これは分数で表すことができません。
循環小数は分数で表すことができます。
根号を含む式の計算
無理数でも根号を使って表す無理数と\(\,\pi\,\)などの根号を使わない数があります。
根号(ルート)を使った計算は中学でもやっていますが、
数学\(\,\mathrm{Ⅰ}\,\)での無理数計算は分数計算や求値問題が主な内容です。
対称式の求値問題が多いので基本対称式の値をよく利用します。
ただ、ほとんどは中学でやってますので、
有理化だけ練習しておけば計算法則は同じです。
2重根号
例えば、
\(\hspace{10pt}\sqrt{5+2\sqrt{6}}\)
のように根号の中に重ねてある根号を2重根号といいます。
2重根号のある数を1重の根号を含む式に変形することを、
「2重根号を外す」
といいます。
慣れればたいしたことはありません。
1次不等式
不等式は数の大小を表すものなので実数に限られます。
1次不等式については中学でも学んでいるので基本的な部分は省略します。
不等式の性質
\(\color{red}{\fbox{ 不等式の性質 }}\)
\(\,\mathrm{A\,<\,B}\hspace{10pt}\)ならば\(\hspace{10pt}\mathrm{A+C\,<\,A+B}\,\)
\(\,\mathrm{A\,<\,B}\hspace{10pt}\)ならば\(\hspace{10pt}\mathrm{A-C\,<\,A-B}\,\)
正の数負の数を足しても大小関係は変わりません。
\(\,\mathrm{A\,<\,B\,,\,C\,>\,0}\hspace{10pt}\)ならば\(\displaystyle \hspace{10pt}\mathrm{AC<BC\,,\,\frac{A}{C}\,<\,\frac{B}{C}}\,\)
正の数を掛けても、正の数で割っても大小関係は変わりません。
\(\,\mathrm{A\,<\,B\,,\,C\,<\,0}\hspace{10pt}\)ならば\(\displaystyle \hspace{10pt}\mathrm{AC<BC\,,\,\frac{A}{C}\,>\,\frac{B}{C}}\,\)
負の数を掛けたり、負の数で割ると大小関係は逆になります。
1次不等式の解き方
上の不等式の性質を利用すれば方程式と解き方は同じです。
方程式と同じように分数の不等式の場合も分母を無くすことからはじめると早いです。
連立不等式
不等式をいくつか連立させたものを連立不等式といいます。
連立不等式を解く場合は、それぞれの不等式を解き、
解は「かつ」で交わりを見ます。
数直線を書くことをおすすめします。
自然数や整数の数を間違えることが多くなる上に、
文字を含んだ問題に対応できなくなります。
絶対値を含む方程式、不等式
絶対値の定義は中学で済ませてありますが、
実数\(\,x\,\)の絶対値についての定義を改めてしておきます。
\(\color{red}{\fbox{ 実数の絶対値の定義 }}\)
実数\(\,x\,\)の絶対値\(\,|\,x\,|\,\)は、
数直線上の\(\,x\,\)に対応する点と原点との距離を表す。
定数\(\,a\,\)を\(\,a\,>\,0\,\)とすると次のことが言えます。
\(\hspace{10pt}|\,x\,|=a\) ⇔ \(x=\pm \,a\)
原点からの距離が\(\,a\,\)の点は2つあります。
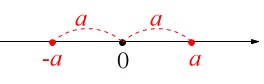
\(\hspace{10pt}|\,x\,|>\,a\) ⇔ \(x\,<\,-a\,,\,a\,<\,x\,\)
原点からの距離が\(\,a\,\)より大きい範囲は2つに分かれます。

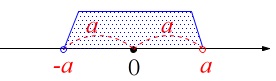
\(\hspace{10pt}|\,x\,|<\,a\) ⇔ \(-a\,<\,x\,<\,a\)
原点からの距離が\(\,a\,\)より小さい範囲は1つです。
数直線を書けばすぐに分かります。
絶対値と場合分け
絶対値記号を外すときの場合分けです。
絶対値は距離を表しているので必ず正の数になります。
よって、絶対値記号は、
絶対値の中が正のときはそのまま外れますが、
\(\hspace{10pt}a\,>\,0\,\)のとき\(\,|\,a\,|=\,a\,\)
絶対値の中が負のときはマイナスを付けて正として外します。
\(\hspace{10pt}a\,<\,0\,\)のとき\(\,|\,a\,|=\,-a\,\)
1次不等式に限らず2次不等式でも同じですよ。
集合と命題
集合は数の集まりですが、中学までは使ったことのない用語や記号が出てきますので少し覚えることが出てきます。
集合
ある条件を満たしているものの集まりを集合といい、
集合を構成している一つひとつのものをその集合の要素といいます。
\(\,a\,\)が集合\(\,A\,\)の要素であることを
\(\hspace{10pt}a\,\in\,A\)
と表します。
※
左に要素を書き、右に集合を書くようにしておいてください。
\(\,a\,\)が集合\(\,A\,\)の要素でないことを
\(\hspace{10pt}a\,\notin\,A\)
と表します。
集合の表し方
集合の表し方はいくつかあるのですべて記憶しておきましょう。
要素を書き並べる方法
\(\,12\,\)の正の約数の集合\(\,A\,\)は
\(\hspace{10pt}A\,=\,\{\,1\,,\,2\,,\,3\,,\,4\,,\,6\,,\,12\,\}\)
このように要素を\(\,\{\hspace{10pt}\}\,\)でくくって表す方法です。
文字を用いて満たすべき条件を示す方法
\(\,12\,\)の正の約数の集合\(\,A\,\)は
\(\hspace{10pt}A\,=\{\,x\,|\,x\,は\,12\,の正の約数\}\,\)
また、集合要素が有限で書き出すことができる集合を有限集合といい、
要素が書き尽くせない集合を無限集合といいます。
例えば、
有限集合:\(\,24\,\)の正の約数
無限集合:正の偶数
などがあります。
不等式で表れる実数の集合も無限集合です。
\(A=\{x\,|\,x\,は\,-1\,<\,x\,<\,1\,を満たす実数\}\)
部分集合
2つの集合\(\,A\,,\,B\,\)を考え、
集合\(\,A\,\)のすべての要素が集合\(\,B\,\)に属しているとき、
\(\,A\,\subset\,B\,\)
と表し、\(\,A\,\)は\(\,B\,\)の部分集合といいます。
※
この部分集合の表し方は真部分集合を意味していますが難しく考えなくて良いです。
2つの集合\(\,A\,,\,B\,\)のすべての要素が一致するときは\(\,A=B\,\)と表します。
\(\,A\,\)が\(\,B\,\)の部分集合で、\(\,A≠B\,\)が分かっているときに
\(\,A\,\)は\(\,B\,\)の真部分集合
というのですが、高校の集合では部分集合は真部分集合を意味しています。
また、要素が1つも無い集合のことを空集合といい、
\(\hspace{10pt}\phi\)(ギリシア語のファイ)
で表します。
※
空集合\(\,\phi\,\)は集合なので\(\,\{\,\phi\,\}\,\)としないように気をつけてください。
集合の共通部分と和集合と補集合
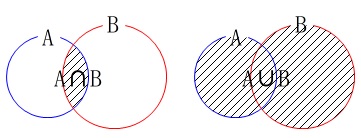
2つの集合\(\,A,B\,\)のどちらにも属する要素の集合を、
\(\,A\,\)と\(\,B\,\)の共通部分または交わりといいます。
記号で\(\,A\,\cap\,B\)と表します。
また、\(\,A\,\)か\(\,B\,\)に属する要素(\(\,A\,\)または\(\,B\,\)の要素)の集合を、
\(\,A\,\)と\(\,B\,\)の和集合または結びといいます。
記号で\(\,A\,\cup\,B\)と表します。
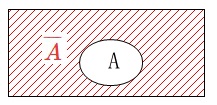
1つの集合の全体集合を\(\,U\,\)と定めて、
\(\,A\,\)の要素ではない\(\,U\,\)の要素全体でできる集合を\(\,A\,\)の補集合\(\,\overline{A}\,\)といいます。
 日本語で説明するとややこしいけど、
日本語で説明するとややこしいけど、
数学の記号や図で表すと一瞬で分かりますよね。
⇒ 集合の記号と意味(要素,真部分集合,和集合,補集合,ド・モルガンの法則)
補集合の性質とドモルガンの法則についてももう一度確認しておいてください。
3つの集合の共通部分と和集合
3つの集合\(\,A,B,C\,\)についても共通部分、和集合、補集合は存在します。
\(\,A,B,C\,\)のすべての共通部分は\(\,A\,\cap\,B\,\cap\,C\,\)と表します。
\(\,A,B,C\,\)の少なくとも1つの要素になっている和集合を\(\,A\,\cup\,B\,\cup\,C\,\)と表します。
命題と条件
命題とは
\(\color{red}{\fbox{ 命題の定義 }}\)
正しいか、正しくないかが定まっている文を命題という。
命題が正しいときその命題は真といい、
命題が正しくないときその命題は偽といいます。
まとめると、真と偽がはっきりと言える文を命題という、ということですね。
条件とは
\(\color{red}{\fbox{ 条件の定義 }}\)
変数\(\,x\,\)を含む文で、\(\,x\,\)に個々の値を代入したとき、
命題となり得るものを\(\,x\,\)に関する条件という。
方程式や不等式はそのものでは命題にはなりません。
しかし、\(\,x\,\)に具体的な値を入れることで命題となります。
例えば、
\(\hspace{10pt}x>3x-5\)
だけでは正しいかどうか定まりません。
しかし、\(\,x=2\,\)であれば真である命題となり、
\(\,x=4\,\)であれば偽である命題になります。
条件\(\,p\,,\,q\,\)において
「\(\,p\,\)ならば\(\,q\,\)である。」
という命題があるとします。
これを矢印を用いて
\(\,p\hspace{10pt}\Rightarrow\hspace{10pt}q\,\)
と書きます。
この命題\(\,p\hspace{4pt}\Rightarrow\hspace{4pt}q\,\)において、
\(\,p\,\)を仮定、\(\,q\,\)を結論
といいます。
命題が「真」であるとは、
\(\,p\hspace{10pt}\Rightarrow\hspace{10pt}q\,\)
が必ず成り立つ必要があります。
1つでも成り立たないものがあれば「偽」になります。
この成り立たせない例を「反例」といいます。
反例が1つでもあればその命題は「偽」であるということです。
必要条件と十分条件
命題\(\hspace{5pt}\,p\hspace{5pt}\Rightarrow\hspace{5pt}q\,\hspace{5pt}\)のように
「\(\,p\,\)ならば\(\,q\,\)」という命題を「ならば命題」ということにすると、
ならば命題\(\hspace{5pt}\,\color{red}{p}\hspace{5pt}\Rightarrow\hspace{5pt}\color{blue}{q}\hspace{5pt}\,\)が真であるとき、
\(\,\color{red}{p}\,\)は\(\,\color{blue}{q}\,\)であるための十分条件である。
また、
\(\,\color{blue}{q}\,\)は\(\,\color{red}{p}\,\)であるための必要条件である。
といいます。
※
誤解しないで欲しいのは、
「\(\hspace{5pt}\,\color{red}{p}\hspace{5pt}\Rightarrow\hspace{5pt}\color{blue}{q}\hspace{5pt}\,\)が真である。」
としたときの仮定と結論の順で十分、必要という条件に付けた名前なので、
真となる命題の順によってどちらかに分かれる場合がありますよ。
詳しくいうと、
命題\(\hspace{5pt}\,p\hspace{5pt}\Rightarrow\hspace{5pt}q\,\hspace{5pt}\)が真であるとき、
\(\,p\,\)は\(\,q\,\)であることを保証するのに十分な条件
\(\,q\,\)は\(\,p\,\)の成立にともなって必然的に成り立つ必要な条件
なのです。(余計分からなくなる?笑)
例えば、
\(\,x=1\,\) ⇒ \(\,x^2=1\,\)
は「真」です。
このとき、\(\,x=1\,\)なら十分に\(\,x^2=1\,\)です。
また、\(\,x^2=1\,\)であることは\(\,x=1\,\)であるためには必要な条件です。
もう少し、
\(\,x\,<\,1\,\) ⇒ \(\,x\,<\,4\,\)
は「真」です。
このとき、\(\,x\,<\,1\,\)ならば\(\,x\,<\,4\,\)を十分に満たしています。
また、\(\,x\,<\,4\,\)は\(\,x\,<\,1\,\)であるためには必要な条件です。
つまり、乱暴な良い方をすれば必要条件の方が広い。
同値と必要十分条件
命題
\(\,p\hspace{10pt}\Rightarrow\hspace{10pt}q\,\)
\(\,q\hspace{10pt}\Rightarrow\hspace{10pt}p\,\)
がともに真であるとき、
\(p\hspace{10pt}⇔\hspace{10pt}q\)
と表し、\(\,p\,\)と\(\,q\,\)は同値であるといいます。
このとき、
「\(\,p\,\)は\(\,q\,\)であるための必要十分条件である。」
または
「\(\,q\,\)は\(\,p\,\)であるための必要十分条件である。」
となります。
条件の否定
条件\(\,p\,\)に対し、
「\(\,p\,\)ではない」という条件を\(\,p\,\)の否定」
といい、\(\,\overline{\,p\,}\,\)と表します。
\(\,p\,\)の否定が\(\,\overline{\,p\,}\,\)なので、
\(\,\overline{\,p\,}\,\)の否定は\(\,p\,\)となります。
例えば、
「有理数である」の否定は「無理数である」
であり、
「無理数である」の否定は「有理数である」
ということです。
「\(\,A\,\)である」の否定\(\overline{\,A\,}\)を定めることは容易ではありませんが、
数直線やベン図を使うと分かり易くなりますよ。
条件の「かつの否定」と「またはの否定」
条件\(\,p\,,\,q\,\)に対し
「\(\,p\,\)かつ\(\,q\,\)」の否定は「\(\,\overline{\,p\,}\,\)または\(\,\overline{\,q\,}\,\)」
「\(\,p\,\)または\(\,q\,\)」の否定は「\(\,\overline{\,p\,}\,\)かつ\(\,\overline{\,q\,}\,\)」
つまり、
\(\overline{ p\,\color{red}{かつ}\,q }\) ⇔ \(\,\overline{\,p\,}\,\)または\(\,\overline{\,q\,}\,\)
\(\overline{ p\,\color{blue}{または}\,q }\) ⇔ \(\,\overline{\,p\,}\,\)かつ\(\,\overline{\,q\,}\,\)
ということです。
注意して欲しいことがあります。
数学で使う「かつ」「または」は日常生活で使っているものとは少し違っています。
⇒ 数学1A 命題と逆に使う「かつ」と「または」と日常生活の違い
数学での使い方を覚えてください。
命題とその逆、裏、対偶
命題「\(\,p\,\)ならば\(\,q\,\)」には仮定と結論を入れかえた「逆」と呼ばれる命題があります。
他にも「裏」と「対偶」があるので真偽の一致とともにまとめておきます。
命題\(\,\color{red}{p}\hspace{4pt}\Rightarrow \hspace{4pt}\color{blue}{q}\,\)に対し、
\(\,\color{blue}{q}\hspace{4pt}\Rightarrow \hspace{4pt}\color{red}{p}\hspace{6pt}\)を\(\hspace{6pt}\color{red}{p}\hspace{4pt}\Rightarrow \hspace{4pt}\color{blue}{q}\hspace{6pt}\)の逆
(仮定と結論を入れかえた命題)
\(\,\color{red}{\overline{\,p\,}}\hspace{4pt}\Rightarrow \hspace{4pt}\color{blue}{\overline{\,q\,}}\hspace{6pt}\)を\(\hspace{6pt}\color{red}{p}\hspace{4pt}\Rightarrow \hspace{4pt}\color{blue}{q}\hspace{6pt}\)の裏
(仮定を否定し、結論も否定した命題)
\(\,\color{blue}{\overline{\,q\,}}\hspace{4pt}\Rightarrow \hspace{4pt}\color{red}{\overline{\,p\,}}\hspace{6pt}\)を\(\hspace{6pt}\color{red}{p}\hspace{4pt}\Rightarrow \hspace{4pt}\color{blue}{q}\hspace{6pt}\)の対偶
(裏の逆命題)
といい、
命題とその逆は真偽は必ずしも一致しないが、
命題とその対偶は真偽が一致する。
また、逆と裏も真偽は一致する。
命題と証明
命題と対偶は真偽が一致するので、
命題が真であることを証明するときに、
(命題の証明が直接しにくいとき)
対偶が真であることをいえば証明したことになります。
この証明方法を「対偶証明法」または簡単に「対偶法」といいます。
「論理」分野での証明で(日本語が長い問題文が多い)、
「証明しにくい」と感じたら対偶法を思い出すと良いです。
証明法にはこの後の「背理法」もありますが、
どちらかというと「なんか当たり前すぎて証明しにくい」と感じることを証明するのに対偶法を使うことが多いです。
背理法は「~ではないことを証明せよ。」と言い換えられる問題でよく使います。
(直接「~ではないことを証明せよ」とは書いていないのが普通です。)
無理数であることの証明(背理法)
命題の証明方法の1つ背理法の論法を簡単にまとめます。
背理法とは
背理法とはある命題を証明したいとき、
命題が偽であると仮定すると矛盾が生じる
ことを証明方法です。
つまり、
成立するはずがないことが導かれて、
命題が偽であるという仮定が成立しない、
だから命題が真である。
ことを断定して良いという論法になります。
背理法のことを「矛盾による証明法」というのを知れば納得いくでしょう。
背理法によって導かれる有名な定理を1つ紹介して終わりとします。
\(\color{red}{\fbox{ ユークリッドの素数定理 }}\)
素数は無数に存在する。
証明は、素数が有限個であると仮定することから始まりますが、
省略します。笑(それほどややこしいものでもありません。)
無理数の証明
無理数とは有理数ではない実数です。
無理数の証明は背理法によって証明しますが、
「ある数が有理数であると仮定する。」
と矛盾が生じることを示します。
このとき、「有理数であると仮定する」というのは、
「無理数ではないと仮定する」ことと同じです。
つまり、上で軽く触れていた
「~ではないことを証明せよ。」
と問題が置き換えることができる証明問題だということです。
無理数であることの証明は、
有理数を\(\,\displaystyle \frac{n}{m}\,(\,m\,,\,n\,は自然数\,)\)
とおいて矛盾を示す場合が普通です。
有理数を\(\,r\,\)とおいて解決する場合もありますが、
有理数は自然数を用いて分数で置く方が普通だと考えておいてください。
具体的な証明の例は別に記事に(いつか)する予定です。
以上です。
はやり、数学\(\,\mathrm{Ⅰ}\,\)でまとめるとなると限界があります。
できれば数学\(\,\mathrm{Ⅱ}\,\)までを一通り見ておいてから、
自分なりに体系化して見ると良いかもしれませんよ。
⇒ 共通テスト(センター試験)数学の勉強法と対策まとめ単元別攻略と解説
数学\(\,Ⅱ\,\)の要点はすべての分野を共通テスト対策の中でまとめてあります。