条件付き確率の公式を使う問題の見分け方は説明してありますので、ここでは公式を使った実際の問題を解いてみましょう。
公式を使わずに答を出す計算方法もあるので説明しておきます。
公式を使っていなくても答はおなじですし、簡単だけど結局は公式そのものの計算だということも分かるでしょう。
条件付き確率の意味と公式
問題は「条件付き確率の見分け方」のものと同じです。
白玉3個と赤球2個が入っている袋から、球を1個ずつもとに戻さないで取り出すことを繰り返すとき、次の確率を求めよ。
(1)1回目も2回目も白玉を取り出す確率
(2)2回目に白玉を取り出したとき、1回目も白玉を取り出していた確率
(3)2回目に白玉を取り出したとき、3回目に赤球を取り出す確率
条件付き確率ですが、確率の乗法定理を使います。
まずは用語の確認をしておきます。
条件付き確率:
事象Aが起こった(確率 \(P(A)\) )という条件のもとで事象Bの起こる確率を、
Aが起こったときのBの起こる条件付き確率といって \( P_A (B)\) で表します。
これは一般に、
\(\displaystyle P_A(B)=\frac{n(A\cap B)}{n(A)}\) ・・・①
で求めることができます。
どういうことかと言うと、条件付き確率 \( \color{red}{P_A (B)}\) は、
「事象Aを全事象と考えたときの、事象 \( \color{red}{A\cap B}\) の起こる確率」
ということです。
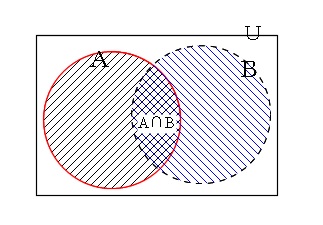
(Aに対する \( A\cap B\) の比率)
この意味を理解しておくことが重要なのですが、計算出来ればまずは良しとします。
条件付き確率の変形
ここは変形しているだけなので飛ばしてかまいません。
全事象をUとして、①の右辺の分母、分子を \( n(U)\) で割って
\(\displaystyle \color{red}{P_A(B)=\frac{P(A\cap B)}{P(A)}}\) が得られます。(公式です)
これから、確率の乗法定理:
\(\color{red}{P(A\cap B)=P(A)\cdot P_A(B)}\)
が成り立ちます。 これは順序を変えても成り立ちます。
つまり、事象Bが起こったときのAという事象の起こる確率も、AとBを入れかえて、
\( \color{red}{P(A\cap B)=P(B)\cdot P_B(A)}\) という乗法定理が成り立つのです。
\(\displaystyle P(A\cap B)=\frac{n(A\cap B)}{n(U)}=\frac{n(A)}{n(U)}\cdot \frac{n(A\cap B)}{n(A)}=P(A)\cdot P_A(B)\)
と同様に、
\(\displaystyle P(A\cap B)=\frac{n(A\cap B)}{n(U)}=\frac{n(B)}{n(U)}\cdot \frac{n(A\cap B)}{n(B)}=P(A)\cdot P_B(A)\)
と示せます。
まとめると、
\( \color{red}{P(A\cap B)=P(A)\cdot P_A(B)=P(B)\cdot P_B(A)}\)
(ベン図で確認して同じだと感じてもらえたら十分です。)
さて、定理、公式が使えれば良いのですが、ここが少し分かりにくいところなのでもう少し説明します。
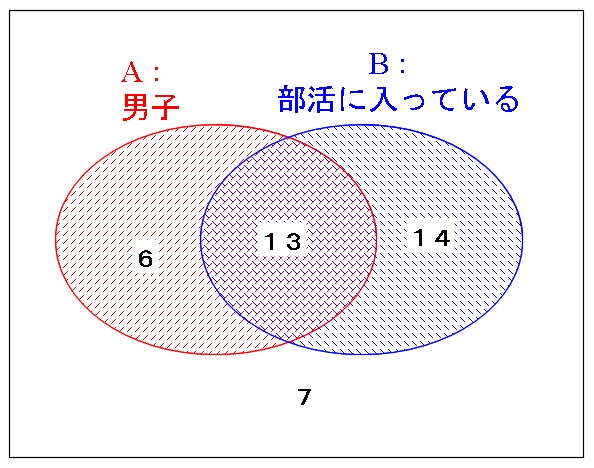
例えば、40人のクラスで、
部活動に入っている男子が13人、入っていない男子は6人。
部活動に入っている女子が14人、入っていない女子は7人。
の場合で見てみます。
男子を選ぶという事象をA、部活に入っているという事象をBとすると、
男子は40人中19人なので
\(\displaystyle P(A)=\frac{\color{blue}{13}+\color{green}{6}}{40}=\frac{19}{40}\)
部活に入っている確率は、男女合わせて27人なので、
\(\displaystyle P(B)=\frac{\color{blue}{13}+\color{red}{14}}{40}=\frac{27}{40}\)
ですが、
選んだ人が男子であったとき、部活に入っている確率 \( P_A(B)\) は男子19人中の13人なので、
\(\displaystyle P_A(B)=\frac{\color{blue}{13}}{\color{blue}{13}+\color{green}{6}}=\frac{13}{19}\)
です。
選んだ人が部活に入っている人で、男子であったときの確率 \( P_B(A)\)は、部活に入っている人27人中13人なので、
\(\displaystyle P_B(A)=\frac{\color{blue}{13}}{\color{blue}{13}+\color{red}{14}}=\frac{13}{27}\)
表にすると
| 男子 | 女子 | 計 | |
| 部活あり | 13 | 14 | 27 |
| 部活なし | 6 | 7 | 13 |
| 計 | 19 | 21 | 40 |
少しはわかりやすくなりますか?
\( P(A)\) :男子は40人中19人
\( P(B)\) :部活に入っているのは40人中27人
\(P_A(B)\) :男子で部活に入っているのは19人中13人
\( P_B(A)\) :部活に入っている男子は27人中13人
ということです。
乗法定理で確認すると、
\(\displaystyle P(A\cap B)=P(A)\cdot P_A(B)=\frac{19}{40}\cdot \frac{13}{19}=\frac{13}{40}\)
\(\displaystyle P(A\cap B)=P(B)\cdot P_B(A)=\frac{27}{40}\cdot \frac{13}{27}=\frac{13}{40}\)
と同じ結果になります。
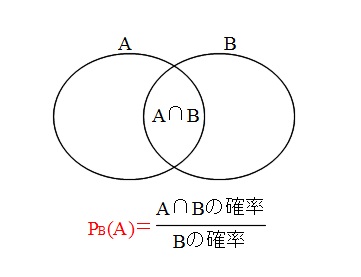
条件付き確率をベン図で解く
ベン図(要素ではなく要素の個数を書き込んであります)で説明すると、
交わりの部分 \( n(A\cap B)=13\) を \( n(A)=19\) で割ったものが
\(\displaystyle P_A(B)=\frac{13}{19}\)
交わりの部分 \( n(A\cap B)=13\) を \( n(B)=27\) で割ったものが
\(\displaystyle P_B(A)=\frac{13}{27}\)
では、問題を解いて行きます。もう一度問題を書き出しておきます。
白玉3個と赤球2個が入っている袋から、球を1個ずつもとに戻さないで取り出すことを繰り返すとき、次の確率を求めよ。
(1)1回目も2回目も白玉を取り出す確率
(2)2回目に白玉を取り出したとき、1回目も白玉を取り出していた確率
(3)2回目に白玉を取り出したとき、3回目に赤球を取り出す確率
「白玉3個、赤球2個」の全体5個から、続けて2個取り出す。
(1)これは簡単です。「も」なので確率の乗法定理です。
1回目白となる確率と、2回目も白となる確率の積で、
\(\displaystyle \frac{3}{5}\cdot \frac{2}{4}=\frac{3}{10}\)
(2)条件付き確率です。
2回目に白玉を取り出す事象をB、1回目に白玉を取り出す事象をAとすると、
「 \( P_B(A)\) を求めよ。」、ということですね。
\( P(B)\) は2回目白を取り出す確率で、
「1回目白」かつ「2回目白」
の場合と、
「1回目赤」かつ「2回目白」
の場合があります。
このことから、
\( P(B)=\displaystyle \frac{3}{5}\cdot \displaystyle \frac{2}{4}+\displaystyle \frac{2}{5}\cdot \displaystyle \frac{3}{4}=\displaystyle \frac{3}{5}\)
(1)から \( P(A\cap B)\) は計算してあるので、公式を使うと、
\( P_B(A)=\displaystyle \frac{P(A\cap B)}{P(B)}=\displaystyle \frac{\displaystyle \frac{3}{10}}{\displaystyle \frac{3}{5}}=\displaystyle \frac{3}{10} \div \displaystyle \frac{3}{5}=\displaystyle \frac{3}{10}\times \displaystyle \frac{5}{3}=\displaystyle \frac{1}{2}\)
(3)2回目に白玉を取り出す事象をB、3回目に赤玉を取り出す事象をCとすると、
「 \( P_B(C)\) を求めよ」ということです。
\( P(B)\) はでていますので、\(P(B\cap C)\) を出す必要があります。
\( P(B\cap C)\) は、「2回目白かつ3回目赤」なので、
「1回目→2回目→3回目」が、
「白→白→赤」または「赤→白→赤」
の確率で、
\( P(B\cap C)=\displaystyle \frac{3}{5}\cdot \displaystyle \frac{2}{4}\cdot \displaystyle \frac{2}{3}+\displaystyle \frac{2}{5}\cdot \displaystyle \frac{3}{4}\cdot \displaystyle \frac{1}{3}=\displaystyle \frac{3}{10}\)
よって、
\( P_B(C)=\displaystyle \frac{P(B\cap C)}{P(B)}=\displaystyle \frac{3}{10} \div \displaystyle \frac{3}{5}=\displaystyle \frac{3}{10} \times \displaystyle \frac{5}{3}=\displaystyle \frac{1}{2}\)
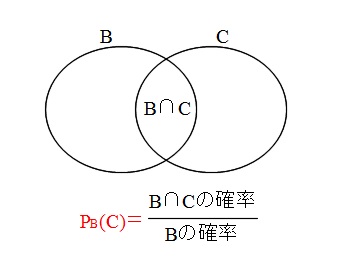
条件付き確率を求める公式を利用すれば計算はできると思いますが、ベン図を使うと公式は必要ありませんよ。
「交わり部分を条件がつく部分で割る」
それだけです。
こちらからのつながりですので確認しておくといいでしょう。