2018年、平成30年度のセンター試験数学ⅡBの第1問の解答と解説です。
三角関数と指数・対数の問題になりますが解説は模範解答とはいえませんので、きれいな解答が見たい人は出版社などの解説を参考にして下さい。
長くなってまとまりがよくない、見にくい、ということで1問ずつ分けることにしました。
問題は大学入試センターにもあります。
問題を印刷して自分で解きながら見て下さい。
第1問(必答)〔1〕三角関数
(1)
1ラジアンとは,\( \fbox{ア}\) のことである。
弧度法の単位「ラジアンの定義」です。
単位円において弧の長さが1となる中心角を1ラジアンといいます。
単位円は半径が1の円のことなので、\(l\) の弧に対する中心角は \( l\) ラジアンになります。
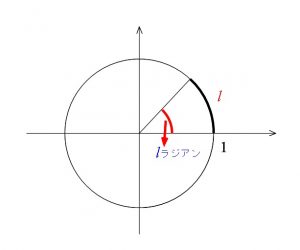
ア:②
定義を覚えていないとき、
ここでは知っているラジアンの関係式を書いて見て、1ラジアンがどうなっているかを見てみれば良いです。
これは知っているだろうというのは
\( 2\pi(radian)=360^{\circ} \hspace{5pt} \Leftrightarrow \hspace{5pt} 1(radian)=\displaystyle \frac{180^\circ}{\pi}\)
ですね。
問題文から関係式(比例式)をつくって見ましょう。
中心角を \( x(radian)\) とすると \(\color{red}{ x=1}\) となるものが正解です。
⓪:半径1の円の面積 \( (\pi r^2)\) は \( \pi\) なので、
中心角 \( 2\pi(radian)\) のとき面積 \( \pi\)
中心角 \( x(radian)\) のとき面積 \( 1\)
を比例式にすると、
\( 2\pi:\pi=x:1 \hspace{5pt} \Leftrightarrow \hspace{5pt} \pi x=2\pi \hspace{5pt} \Leftrightarrow \hspace{5pt} x=2\)
①:半径 \( \pi\) の面積は \( \pi^3\) なので、
中心角 \( 2\pi(radian)\) のとき面積 \( \pi^3\)
中心角 \( x(radian)\) のとき面積 \( 1\)
を比例式にすると、
\( 2\pi:\pi^3=x:1 \hspace{5pt} \Leftrightarrow \hspace{5pt} \pi^3 x=2\pi \hspace{5pt} \Leftrightarrow \hspace{5pt} x=\displaystyle \frac{2}{\pi^2}\)
②:半径1の円周の長さ \( (2\pi r)\) は \( 2\pi\) なので、
中心角 \( 2\pi(radian)\) のとき円周 \( 2\pi\)
中心角 \( x(radian)\) のとき弧の長さ \( 1\)
を比例式にすると、
\( 2\pi:2\pi=x:1 \hspace{5pt} \Leftrightarrow \hspace{5pt} 2\pi x=2\pi \hspace{5pt} \Leftrightarrow \hspace{5pt} x=1\)
ここで正解が出ましたが一応続けます。
③:半径 \( \pi\) の円周の長さは \( 2\pi^2\) なので、
中心角 \( 2\pi(radian)\) のとき円周 \( 2\pi ^2\)
中心角 \( x(radian)\) のとき弧の長さ \( 1\)
を比例式にすると、
\( 2\pi:2\pi^2=x:1 \hspace{5pt} \Leftrightarrow \hspace{5pt} 2\pi^2 x=2\pi \hspace{5pt} \Leftrightarrow \hspace{5pt} x=\displaystyle \frac{1}{\pi}\)
説明すると長いですが比例式を書き出すだけならすぐ終わりますよ。
(2)
弧度法 \( \leftrightarrow \) 度分法の書き換え問題です。
これは
\( 2\pi=360^\circ\)
から簡単に出せます。
\(144^\circ\) を弧度で表すと
比例式がやりやすいです。(「°」はなくて良いので省略します。)
\( 360:2\pi=144:x\\ \\
\hspace{5pt} \Leftrightarrow \hspace{5pt} 360x=144\pi \\ \\
\hspace{5pt} \Leftrightarrow \hspace{5pt} x=\displaystyle \frac{2\times144}{360}\pi\\ \\
\hspace{5pt} \Leftrightarrow \hspace{5pt} x=\displaystyle \frac{\fbox{4}}{\fbox{5}}\pi\)
また,\(\displaystyle \frac{23}{12}\pi\) ラジアンを度で表すと
これも比例式を解けば良いだけです。
\( 2\pi:360=\displaystyle \frac{23}{12}\pi:x\\ \\
\hspace{5pt} \Leftrightarrow \hspace{5pt} 2\pi x=360\times \displaystyle \frac{23}{12}\pi \\ \\
\hspace{5pt} \Leftrightarrow \hspace{5pt} x=\displaystyle \frac{360\times 23}{2\times 12}\\ \\
\hspace{5pt} \Leftrightarrow \hspace{5pt} x=15\times 23\\ \\
\hspace{5pt} \Leftrightarrow \hspace{5pt} x=\fbox{345}\)
イ:4 ウ:5 エオカ:345
(3)
この問題は目的を示してくれているので問題の意図が分かりやすいですね。
誘導に乗らなくても求まりますが、誘導に乗りましょう。
\(\displaystyle \color{red}{\frac{\pi}{2} ≦ \theta ≦ \pi}\) ・・・⓪
は後で使うはずなので問題用紙に大きく印をしておきます。
\(\displaystyle 2\sin\left(\theta+\frac{\pi}{5}\right)-2cos\left(\theta+\frac{\pi}{30}\right)=1\) ・・・①
において
\( x=\theta+\displaystyle \frac{\pi}{5}\)
とおくことで変形するように誘導されています。
\(\displaystyle \sin\left(\theta+\frac{\pi}{5}\right)\) の部分はそのまま \( \sin x\) とおけて、
変わるのは \(\displaystyle \cos\left(\theta+\frac{\pi}{30}\right)\) の部分だけで、
\( \theta+\displaystyle \frac{\pi}{30}=\theta +\displaystyle \frac{\pi}{5}+\alpha\)
と見れば、通分することで見やすくなりますが、
\( \displaystyle \frac{\pi}{30}=\displaystyle \frac{\pi}{5}+\alpha\\ \\
\Leftrightarrow \hspace{5pt} \alpha=\displaystyle \frac{\pi}{30}-\displaystyle \frac{\pi}{5}=\displaystyle \frac{1\pi-6\pi}{30}=-\displaystyle \frac{\pi}{6}\)
改めて書き直すと、
\( \theta+\displaystyle \frac{\pi}{30}=\theta+\displaystyle \frac{\pi}{5}-\displaystyle \frac{\pi}{6}=x-\displaystyle \frac{\pi}{6}\)
①は
\( 2\sin x-2\cos\left(x-\displaystyle \frac{\pi}{\fbox{6}}\right)=1\)
加法定理
加法定理を用いると
\( \sin x\) の係数が変わっているけど、どこに加法定理?って悩まないように、
加法定理が使える部分だけを処理しましょう。
加法定理と合成は三角関数の二大テーマです。
時間を惜しまずこれを書き出せば歴代のセンター試験はおおよそクリアーできますよ。
加法定理
\( \color{red}{\sin(\alpha+\beta)=\sin\alpha \cos\beta+\cos\alpha\sin\beta} \)
\( \color{red}{\cos(\alpha+\beta)=\cos\alpha \cos\beta-\sin\alpha\sin\beta}\)
この2つでも事足りますが、
\( \color{red}{\sin(\alpha-\beta)=\sin\alpha \cos\beta-\cos\alpha\sin\beta }\)
\( \color{red}{\cos(\alpha-\beta)=\cos\alpha \cos\beta+\sin\alpha\sin\beta }\)
これを参考にしながら展開すればいいだけです。
\( \cos\left(x-\displaystyle \frac{\pi}{6}\right)\\ \\
=\cos x\cdot \cos\displaystyle \frac{\pi}{6}+\sin x\cdot \sin\displaystyle \frac{\pi}{6}\\ \\
=\underline{\displaystyle \frac{\sqrt{3}}{2}\cdot \cos x+\displaystyle \frac{1}{2}\cdot \sin x}\)
これを
\( 2\sin x-2\underline{\cos\left(x-\displaystyle \frac{\pi}{6}\right)}=1\)
にあてはめると
\( 2\sin x-2\left(\underline{\displaystyle \frac{\sqrt{3}}{2}\cdot \cos x+\displaystyle \frac{1}{2}\cdot \sin x}\right)=1\\ \\
\Leftrightarrow \hspace{5pt} 2\sin x-\sqrt{3}\cos x-\sin x=1\\ \\
\Leftrightarrow \hspace{5pt} \sin x-\sqrt{\fbox{3}}\cos x=1\)
キ:6 ク:3
おきまりの加法定理でした。
三角関数の合成
次は合成です。
\( \color{red}{a\sin x+b\cos x=\sqrt{a^2+b^2}\sin(x+\alpha)}\)
と変形するヤツです。
これが今の段階でできていないなら三角関数はやり直して下さい。
できなければならないものなのです。
\( \sin x-\sqrt{3}\cos x\\ \\
=2\left(\sin x\cdot \displaystyle \frac{1}{2}-\cos x\cdot \displaystyle \frac{\sqrt{3}}{2}\right)\\ \\
=2\left(\sin x\cdot \cos\displaystyle \frac{\pi}{3}-\cos x\cdot \sin\displaystyle \frac{\pi}{3}\right)\\ \\
=2\sin\left(x-\displaystyle \frac{\pi}{3}\right)\)
加法定理を逆にたどれば簡単です。
\( \sin x-\sqrt{3}\cos x=2\sin\left(x-\displaystyle \frac{\pi}{3}\right)\)
に慣れている人はそのままで良いですよ。
途中過程なんか必要無し、ここでも聞いていないでしょう?
よって「合成を用いると」
\( \sin x-\sqrt{3}\cos x=1\\ \\
\Leftrightarrow \hspace{5pt} 2\sin\left(x-\displaystyle \frac{\pi}{3}\right)=1\\ \\
\Leftrightarrow \hspace{5pt} \sin\left(x-\displaystyle \frac{\pi}{\fbox{3}}\right)=\displaystyle \frac{1}{\fbox{2}}\)
ケ:3 コ:2
これからこの方程式を満たす \( x\) を先に求めますが、
ここは適当に \( x\) をいくつか決めて後で条件に合う \(\theta\) を選んで良いです。
例えば、
\( x-\displaystyle \frac{\pi}{3}=\displaystyle \frac{\pi}{6}\hspace{5pt},\hspace{5pt}\displaystyle \frac{5\pi}{6}\)
から
\( x=\displaystyle \frac{\pi}{3}+\displaystyle \frac{\pi}{6}\hspace{5pt},\hspace{5pt}\displaystyle \frac{\pi}{3}+\displaystyle \frac{5\pi}{6}=\displaystyle \frac{\pi}{2}\hspace{5pt},\hspace{5pt}\displaystyle \frac{7\pi}{6}\)
となります。
\(\displaystyle x=\theta+\frac{\pi}{5}\) なので
\( \theta+\displaystyle \frac{\pi}{5}=\displaystyle \frac{\pi}{2}\hspace{5pt},\hspace{5pt}\displaystyle \frac{7\pi}{6}\)
を解くと、
\( \theta=\displaystyle \frac{3}{10}\pi\hspace{5pt},\hspace{5pt}\displaystyle \frac{29}{30}\pi\)
このうち⓪を満たすのは、
\( \theta=\displaystyle \frac{\fbox{29}}{\fbox{30}}\pi\)
忘れてないですよね、
\(\displaystyle \frac{\pi}{2}≦ \theta ≦ \pi\) ・・・⓪
でした。
サシ:29 スセ:30
〔2〕指数・対数関数
やはり指数対数は誘導なしでも方針は決まります。
方針の立て方はまだ記事にしていなかったと思うので、問題に合わせて説明します。
\(\displaystyle x^{log_3 x}≧\left(\frac{x}{c}\right)^3\) ・・・②
こういった指数と対数が入り乱れた式を見たら、
対数に統一することと、底をそろえることを意味なく思えても実行します。
底は \( x\) にもできますが、底に文字って嫌な感じがするので定数にしたいところです。
不等式の中で、\( log_3 x\) という部分があるので底を3で統一します。
両辺の底を3として対数をとると
\( x^{log_3 x}≧ \left(\displaystyle \frac{x}{c}\right)^3\\ \\
\Leftrightarrow \hspace{5pt} \log_3(x^{log_3 x})≧ log_3\left(\displaystyle \frac{x}{c}\right)^3\\ \\
\Leftrightarrow \hspace{5pt} \log_3 x^{(log_3x)} ≧ 3(log_3 x-log_3 c)\\ \\
\Leftrightarrow \hspace{5pt} (log_3 x)^2 ≧ 3(log_3 x-log_3 c)\)
ここまでは誘導を見なくてもやっておくと誘導に乗りやすいはずです。
続きを見ずにやるとこうなりますが、
問題では3を底とする対数をとるように誘導がありました。w
さらに、左辺に全部を集めるようなので
\( (log_3 x)^2-3(log_3 x-log_3 c)≧ 0\\ \\
\Leftrightarrow \hspace{5pt} (log_3 x)^2-3log_3 x+3log_3 c≧ 0\)
ここで \( t=log_3x\) とおくと
\( t^{\fbox{2}}-\fbox{3}t+\fbox{3}log_3 c≧ 0 \) ・・・③
\( c=\sqrt[3]{9}\)
根号は便利な記号ですが計算過程ではあまり使いません。
指数関数、対数関数をやるんだから根号はなくして指数に統一するように直せば良いでしょう。
\( c=\sqrt[3]{9}=\sqrt[3]{3^2}=(3^2)^{\displaystyle \frac{1}{3}}=(3)^{\displaystyle \frac{2}{3}}\)
このとき③は
\( t^2-3t+3log_3c\\ \\
=t^2-3t+3log_3(3)^{\displaystyle \frac{2}{3}}\\ \\
=t^2-3t+3\cdot \displaystyle \frac{2}{3} log_33\\ \\
=t^2-3t+2≧ 0\)
なので
\( (t-1)(t-2)≧ 0 \hspace{5pt} \Leftrightarrow \hspace{5pt} t≦ \fbox{1} \hspace{5pt},\hspace{5pt} t ≧ \fbox{2}\)
(普通なら数直線に沿って \( t≦ 1 \hspace{5pt},\hspace{5pt} 2 ≦ t\) )
チ:1 ツ:2
これは \( x\) の条件に戻すと
\( log_3 x≦ 1 \hspace{5pt} \Leftrightarrow \hspace{5pt} x≦ 3\)
\( log_3 x≧ 2 \hspace{5pt} \Leftrightarrow \hspace{5pt} 9≦ x\)
かつ、真数条件より
\( 0 < x\)
よって
\( 0 < x ≦ 3\hspace{5pt},\hspace{5pt} 9≦ x\)
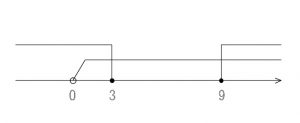
問題の回答欄では順序が違っていて、
\( \fbox{0} < x ≦ \fbox{3}\hspace{5pt},\hspace{5pt} x≧ \fbox{9}\)
テ:0 ト:3 ナ:9
「次に,②が \( x > 0\) の範囲でつねに・・・」
と続きますが、問題用紙でこの「テ」の四角は囲み枠の腺が細くなっていますよね。
この場合、すでに答は出てるので考える必要はありませんが、入る数字が同じなので放っている人がいますが、同じ数字を書き込んで下さい。
「テ」は関係ないんです。
数字を書き込んで流れを見ないと分かりにくいです。
こんなことはセンター対策をはじめたときに学校で注意があったかもしれませんが、
センター試験受験生なら当たり前としておきましょう。
問題に戻りましょう。
\(x>0\) の範囲で \( t\) のとり得る範囲は?
\(t\) は何かというと \( t=log_3 x\) です。
軸を \( x-t\) で書くと、単調増加します。
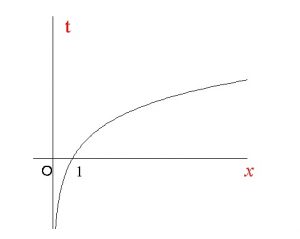
よって、\( t\) は実数全体の値をとります。
ニ:②
この範囲の \( t\) に対して,③がつねに成り立つための必要十分条件は、
この範囲とは 「 \( t\) が実数全体を動くとき」です。
③
\( t^{2}-3t+3log_3 c≧ 0 \)
がすべての実数 \(t\) に対して成り立つ。
2次関数で考えれば簡単です。
というより、置換した後は2次関数の問題になっているのは普通です。
\( f(t)=t^2-3t+3log_3c\)
の頂点の座標は
\( f(t)=t^2-3t+3log_3c\\ \\
=\left(t-\displaystyle \frac{3}{2}\right)^2-\displaystyle \frac{9}{4}+3log_3c\)
から
\( \left(\displaystyle \frac{3}{2} \hspace{5pt},\hspace{5pt}-\displaystyle \frac{9}{4}+3log_3c\right)\)
条件を満たすには
\( -\displaystyle \frac{9}{4}+3log_3c≧ 0\)
となっていればいいのです。
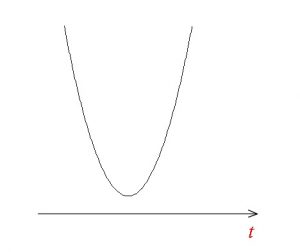
\( -\displaystyle \frac{9}{4}+3log_3c≧ 0\\ \\
\Leftrightarrow \hspace{5pt} -9+12log_3c≧ 0\\ \\
\Leftrightarrow \hspace{5pt} 12log_3c≧ 9\\ \\
\Leftrightarrow \hspace{5pt} log_3c≧ \displaystyle \frac{9}{12}=\displaystyle \frac{\fbox{3}}{\fbox{4}}\)
つまり
\( log_3c≧ \displaystyle \frac{3}{4}\hspace{5pt}\Leftrightarrow \hspace{5pt} c≧ 3^{\displaystyle \frac{3}{4}}\)
これでいいともうのですが問題は根号で表すようになっています。
\( c≧ 3^{\displaystyle \frac{3}{4}}\hspace{5pt}\Leftrightarrow \hspace{5pt} c≧ \sqrt[4]{3^3}=\sqrt[\fbox{4}]{\fbox{27}}\)
ヌ:3 ネ:4 ノ:4 ハヒ:27
説明は長くなりましたが、
計算を進めること自体は短時間でできる問題ばかりでした。
第2問に続きます。
⇒ センター試験過去問 2018年(平成30年)度数学ⅡB第2問(微分積分)の解答と解説
数年分見ておくと傾向はつまめます。
普通の解答とは違う?ので使える部分だけ使って下さい。