2018年、平成30年度のセンター試験過去問数学ⅡBの第２問の解答と解説です。
第２問は微分積分ですが（１）（２）に分かれていてそれぞれが別問題となっています。
驚いたのは、グラフの概形を書くところや計算をする場所がないくらい文字がずらずら並んでいるところです。
それほど計算量が多いわけではないにしても、あの小さなところではさらに時間の余裕がなくなったでしょうね。
第２問（必答）微分積分〔１〕微積
問題は大学入試センターにもあります。
計算しなくても誘導で穴埋めできるのかな？
と一瞬だけ思いましたが、面積計算があるところで
「どこで計算しろっての？」（余白が少ない）
と感じた文字量でした。
小さいスペースですが、やるべきことは変わりません。
位置関係が分かるグラフと計算過程をまとめて書いておくことです。
直線 \( y=2x-1\) を \( \ell\) とする。
\( C\) は点 A（１,１）において \( \ell\) と接しているとする。
おおよその位置関係を見ておきましょう。
軸も入れていませんがだいたいこんな感じでしょう。
（１）
この問題は（も）読む前に、やることをやっておかないとつながりにくいです。
\(y=px^2+qx+r\) ･･･①
微分すると
\( y’=2px+q\) ･･･②
これは接線の傾きを表しますね。
点Aにおける接線は \( y=2x-1\) なので傾きは \( \fbox{2}\) なので、
②において \(x=1\) とすると \(2=2p+q\) となるはずです。
\( 2=2p+q \hspace{5pt} \Leftrightarrow \hspace{5pt} q=\fbox{-2}p+\fbox{2}\)
と分かります。
さらに点Aを通ることから①に（１,１）を代入して、
\( 1=p+q+r\)
これと、\( q=-2p+2\) から
\( r=1-p-q=1-p-(-2p+2)=p-\fbox{1}\)
このように条件から分かることを書き出していけば自ずと出てくる数値です。
（２）
\(y=px^2+rx+r\) を \( p\) だけで表すと
\( y=px^2+(-2p+2)x+p-1\)
面積 \( S\) は
読み進めると、接点よりも右の \( y\) 軸に平行な縦の直線だと分かります。
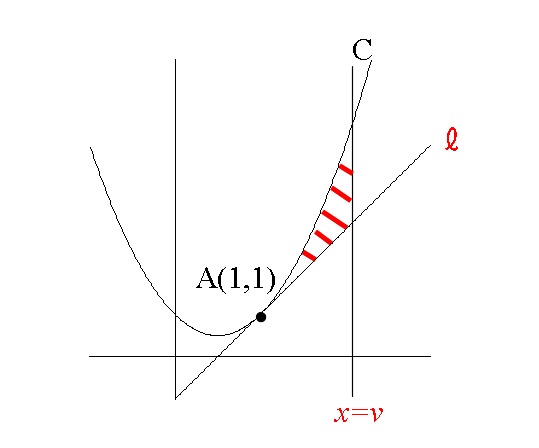
積分区間は \( 1≦ x≦ v\) なので
\( \displaystyle S=\int_1^v\{(px^2+(-2p+2)x+p-1)-(2x-1)\}dx\\ \\
= \int_1^v(px^2-2px+p)dx\\ \\
\displaystyle =\left[\displaystyle \frac{p}{3}x^3-px^2+px \right]_1^v\\ \\
=p\left[\displaystyle \frac{1}{3}x^3-x^2+x \right]_1^v\\ \\
=p\left[\displaystyle \frac{x^3-3x^2+3x }{3}\right]_1^v\\ \\
=\displaystyle \frac{p}{3}\left[x^3-3x^2+3x\right]_1^v\\ \\
=\displaystyle \frac{p}{3}\left\{(v^3-3v^2+3v)-(1-3+3)\right\}\\ \\
=\displaystyle \frac{p}{\fbox{3}}\left(v^3-\fbox{3}v^2+\fbox{3}v-\fbox{1}\right)\)
これをどこで計算しろというのか、老眼が進んでると小さい字が見えにくいんだけど、高校生って目が良いよね。
数学得意な人って、解く人の事は考えないのか、わざとなのか、これを見ていると他の問題をつくった計算スペースをつくってくれている作成者の優しが伝わってきます。
ちなみに別のページのスペースを使うことはできても、行ったり来たりがたいへんじゃなかったですか？
部分的な面積のポイント
次は \( T\) です。
積分では部分的な面積がいくつか出てきますが、記号を使って表すことが多いので、
どこがどの記号で表されているか見分けがつくようにしておくことがポイントになります。
台形です。
台形の面積の公式でもいいです。
ここでは一応積分の形だけはとっておきます。
\( \displaystyle T=\int_1^v(2x-1)dx\\ \\
=\left[x^2-x\right]_1^v\\ \\
=(v^2-v)-(1-1)\\ \\
=v^{\fbox{2}}-v\)
カ：３ キ：３ ク：３ ケ：１ コ：２
続きです。
なんで \( x\) の関数だったのに \( v=2\) で極値？と疑問に思う前に、
\( U=S-T\) を計算しておきましょう。
\( v\) の関数に置き換わっているのです。
\( U=S-T\\ \\
=\displaystyle \frac{p}{3}\left(v^3-3v^2+3v-1\right)-(v^2-v)\)
展開する気がしないのでそのままにしておきます。ｗ
いや、普通は展開するだろうからします。
（微分するので展開しない方が楽ですよ。）
\( U(v)\\ \\
=\displaystyle \frac{p}{3}v^3-pv^2+pv-\displaystyle \frac{p}{3}-v^2+v\\ \\
=\displaystyle \frac{p}{3}v^3+(-p-1)v^2+(p+1)v-\displaystyle \frac{p}{3}\\ \\
=\displaystyle \frac{p}{3}v^3-(p+1)v^2+(p+1)v-\displaystyle \frac{p}{3}\)
極値の条件があるので微分します。
\( U'(v)=pv^2-2(p+1)v+p+1\)
\( v=2\) で極値をとるらしいので、\( U'(2)=0\) となる。
\( U'(2)=p(2)^2-2(p+1)(2)+p+1\\ \\
=4p-4(p+1)+p+1\\ \\
=4p-4p-4+p+1\\ \\
=p-3=0 \hspace{10pt}\\ \\
∴ p=\fbox{3}\)
サ：３
さらに続きます。
\( p=3\) のとき \( U=S-T=0\) つまり 面積 \( S\) と面積 \( T\) が等しくなるときのことですが、グラフ上の意味が無くても計算できます。
\(p=3\) のとき
\( U=S-T=0\\ \\
\hspace{5pt} \Leftrightarrow \hspace{5pt}v^3-4v^2+4v-1=0\)
因数定理を使っても良いですが、接点では面積は両方０なので \(v=1\) はこの方程式の解であると分かります。
\( v^3-4v^2+4v-1=0\\ \\
\hspace{5pt} \Leftrightarrow \hspace{5pt}(v-1)(v^2-3v+1)=0\)
これを解いて
\( v=1\,,\,\displaystyle \frac{3\pm \sqrt{9-4}}{2}\\ \\
=1\,,\,\displaystyle \frac{3\pm \sqrt{5}}{2}\)
このうち \( 1< v\) を満たすのは
\( v=\displaystyle \frac{\fbox{3}+\sqrt{\fbox{5}}}{\fbox{2}}\)
シ：３ ス：５ セ：２
まだ続きます。
これは増減を聞いているので増減表と分かりやすいでしょう。
当然、微分して増減表を書きます。
\( U(v)=v^3-4v^2+4v-1\)
\( U'(v)=3v^2-8v+4\)
\(U'(v)=0\) つまり \( 3v^2-8v+4=0\) から
\( 3v^2-8v+4=0\hspace{5pt} \Leftrightarrow \hspace{5pt}(v-2)(3v-2)=0\)
よって \(\displaystyle v=\frac{2}{3}\,,\,2\) で \( U'(v)=0\) となり増減表は
| \(v\) | \(\cdots\) | \(\left(\frac{2}{3}\right)\) | \(\cdots\) | (1) | \(\cdots\) | 2 | \(\cdots\) | \(\left(\frac{3+\sqrt{5}}{2}\right)\) | \(\cdots\) |
| \(U'(v)\) | + | 0 | – | ( ) | – | 0 | + | ( ) | + |
| \(U(v)\) | \( \nearrow\) | ( ) | \( \searrow\) | (0) | \( \searrow\) | -1 | \( \nearrow\) | 0 | \( \nearrow\) |
全体の増減を見ましたが、定義域内の増減だけでも良いですよ。
（ ）の数値は必要無い値です。
グラフにするともっと分かりやすいです。
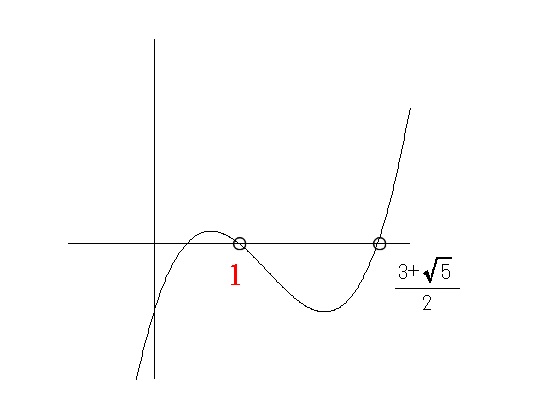
\(1< v < v_0 \) では \(U\) の値は軸より下にあるでしょう。
ソ：③
まだあった。しつこいな。
\( U\) の最小値は \( 1< v\) において増減表から \( v=2\) のとき \( \fbox{-1}\) です。
タチ：－１
第２問（必答）微分積分〔２〕微積
\( t>1\) のとき，曲線 \( y=f(x)\) と \( x\) 軸 おとび２直線 \( x=1\,,\,x=t\) で囲まれた図形の面積を \( W\) とする。
\( t\) が \( t>1\) の範囲を動くとき，\( W\) は，底辺の長さが \( 2t^2-2\) ，
他の２辺の長さがそれぞれ \( t^2+1\) の二等辺三角形の面積とつねに等しいとする。
ここまで来てようやく分かりました。
条件を１つひとつ見て取れているかを試しているんですね。
だらだら読んでも意味が無いことをこの短い文章で示してくれています。
順に読み取ってやるべき作業をしましょう。
\( f(x)\) は \( x≧ 1\) でつねに \( f(x)≦ 0\) ということは、
\( x≧ 1\) ではつねに \( x\) 軸よりも下にあるということです。
形は決まりませんので、積分するときの区間を分けなくて良いということに利用するのでしょう。
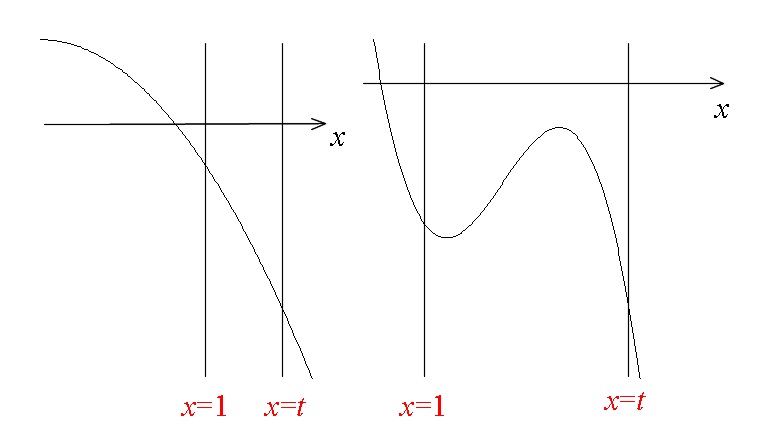
\( t>1\) というのは \( x=t\) という直線が \( x=1\) よりも右にあるということです。
\( x=1\,,\,x=t\) の２つの直線で囲むので右が \( x=t\) とこれも場合分けがなくなります。
これは、
「一般に」という部分はいつでも成り立ちますが、
「 \( W\) 」に関しては
「問題に沿って成り立つ関係をみてみると」
ということなので、条件を書き出してから見た方が良いです。
一般に \( f(x)\) の不定積分を \( F(x)\) とすれば
\( F'(x)=f(x)\)
となることは定義されています。
微分と積分は逆演算ですからね。
\( \displaystyle \int f(x)dx=F(x)+C \)
両辺微分すると
\( f(x)=F'(x)\)
\( W\) は条件通りに積分して見ます。
\( \displaystyle W=\int_1^t(-f(x))dx\\ \\
=-\left[F(x)\right]_1^t\\ \\
=-\left\{F(t)-F(1)\right\}\\ \\
=-F(t)+F(1)\)
ここで答がでていました。
ツ：⑦ テ：④
下の方にまだ続きが、あります。
「したがって」ってまだ \( t\) の具体的な関数は出てません。
\( W\) が「二等辺三角形とつねに等しい」といっているので三角形の面積を出してみましょう。
底辺： \( 2t^2-2\)
他の２辺： \( t^2+1\)
公式を知っているなら別ですが普通は知りませんので図を書いて先ずは高さを出しましょう。
二等辺三角形の頂角の二等分線は底辺を垂直に二等分するので、
高さを \( h\) とすると、三平方の定理から
\( (t^2-1)^2+h^2=(t^2+1)^2\)
これから
\( h^2=(t^2+1)^-(t^2-1)^2\\ \\
=(t^4+2t^2+1)-(t^4-2t^2+1)\\ \\
=4t^2\)
\( ∴ \hspace{5pt}h=2t\)
二等辺三角形の面積は
\( \displaystyle \frac{1}{2}\cdot (2t^2-2)\cdot 2t=2t^3-2t\)
これが \( W\) に等しいから
\( W=-F(t)+F(1)=2t^3-2t\)
微分すると \( F'(1)=0\) なので
\( -f(t)=6t^2-2\\ \\
\hspace{5pt} \Leftrightarrow \hspace{5pt}f(t)=\fbox{-6}\,t^{\,\fbox{2}}+\fbox{2}\)
よって，\( x>1\) における \( f(x)\) が \( f(x)=-6x^2+2\) とわかるのです。
トナ：－６ ニ：２ ヌ：２
関係式を出すときにとっとと計算を進めない時間的にきつくなったかもしれません。
数学ⅡＢではやることやって、迷わず突っ走ることがポイントです。
続いて第３問です。
⇒ センター試験過去問 2018年（平成30年）度数学ⅡB第3問（数列）の解答と解説
\(ⅡB\)の過去問まとめです。
数年分になるので傾向は見られます。
共通テストになっても形式はどうなるか分かりませんが、内容は変わりません。