２０１８年、平成３０年度のセンター試験の過去問、数学ⅠＡの解答と解説です。
ここに書いてある解説は、きれいに解く、というより数学が苦手な人が現場で解答するなら、となりますので美しい解答を求めている人は予備校の解説や数学の得意な人の解説を参考にして下さい。
問題は全部は書きませんので全文は大学入試センターや新聞などの問題を見てください。
第１問（必答）
ここは必答問題なので捨てるところをなるだけ減らしたいところです。
〔１〕「数と式」
\( x\) が実数というのは良いとして、
\( A=x(x+1)(x+2)(5-x)(6-x)(7-x)\)
から問題の最後を見ても何をさせたいのかがさっぱり分からない。
ということで誘導に乗ることを考えましょう。
\( (x+n)(n+5-x)=x(5-x)+n^2+\fbox{ア}n\)
であり、
左辺を展開して右辺の形にするしか無いでしょう。
\( (5-x)\) をまとめて処理する方がはやいですが全部展開します。
\( (x+n)(n+5-x)\\ \\
=xn+5x-x^2+n^2+5n-nx\\ \\
=5x-x^2+n^2+5n\\ \\
=x(5-x)+n^2+\fbox{5}n\)
ア：５
\( A=X(X+\fbox{イ})(X+\fbox{ウエ})\)
と表せるらしいけど、何にしたがったらこうなる？
方法は２つあります。
\( (x+n)(n+5-x)=x(5-x)+n^2+5n\)
において
\( n=0\) のとき
\( (x+0)(0+5-x)=x(5-x)+0^2+5\cdot 0\\ \\
\Leftrightarrow \hspace{10pt}x(5-x)=X\)
\( n=1\) のとき
\( (x+1)(1+5-x)=x(5-x)+1^2+5\cdot 0\\ \\
\Leftrightarrow \hspace{10pt}(x+1)(6-x)=X+6\)
\( n=2\) のとき
\( (x+2)(2+5-x)=x(5-x)+2^2+5\cdot2\\ \\
\Leftrightarrow \hspace{10pt}(x+2)(7-x)=X+14\)
これらを \( A\) にあてはめると
\( A=X(X+\fbox{6})(X+\fbox{14})\)
と誘導してくれた式をうまく使う方法が１つ。
もう一つは、強引に展開して \( x(5-x)=5x-x^2\) をつくる方法です。
パッと見て誘導に気がつかなければこっちで解くでしょう。
「なんのための誘導なんだよ」
と数学が得意なお偉い人にいわれようが、
答を意地でも出そうってときに四の五の言ってられない。
\( A=x(x+1)(x+2)(5-x)(6-x)(7-x)\\ \\
=x(5-x)(x+1)(6-x)(x+2)(7-x)\\ \\
=x(5-x)\{6x-x^2+6-x\}\{7x-x^2+14-2x\}\\ \\
=x(5-x)(5x-x^2+6)(5x-x^2+14)\\ \\
=X(X+\fbox{6})(X+\fbox{14})\)
順番の入替は気がつくと思うので説明無しで処理しましたが、
誘導がじゃまに感じます。
イ：６ ウエ：１４
〔１〕の最後
これも何が言いたいのかわからないけど、
\(\displaystyle x=\frac{5+\sqrt{17}}{2}\) を見たら当サイトではやることを決めているので、答に関係するかどうか知らないけどやる。
\( x=\displaystyle \frac{5+\sqrt{17}}{2}\\ \\
\Leftrightarrow \hspace{10pt} 2x-5=\sqrt{17}\)
両辺平方して根号をなくす。
\( (2x-5)^2=17\\ \\
\Leftrightarrow \hspace{10pt} 4x^2-20x+25=17\\ \\
\Leftrightarrow \hspace{10pt} 4x^2-20x+8=0\\ \\
\Leftrightarrow \hspace{10pt} x^2-5x+2=0 \\ \\
\Leftrightarrow \hspace{10pt} 5x-x^2=X=\fbox{2}\)
うまく答がでるようになっているんですねえ。
\( A=X(X+6)(X+14)\\ \\
=2(2+6)(2+14)\\ \\
=2\cdot 8\cdot 16=2\cdot 2^3 \cdot 2^4=2^{\fbox{8}}\)
オ：２ カ：８
\( X=x(5-x)\) に代入したとしても、大した計算にはなりません。
\( X=\displaystyle \frac{5+\sqrt{17}}{2}\cdot \left(5-\displaystyle \frac{5+\sqrt{17}}{2}\right)\\ \\
=\displaystyle \frac{5+\sqrt{17}}{2}\cdot \displaystyle \frac{10-5-\sqrt{17}}{2}\\ \\
=\displaystyle \frac{5+\sqrt{17}}{2}\cdot \displaystyle \frac{5-\sqrt{17}}{2}\\ \\
=\displaystyle \frac{25-17}{4}=\fbox{2}\)
問題の意味はよくわかりませんが、計算スペースはありがたかったです。
〔２〕昨年と同じ構成で集合と命題
〔２〕集合と命題
（１）
要素はすべて自然数じゃないですか。
書き出すに決まってます。
\( U={1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20}\)
これはいらないんだけど、この中にすべての要素があります。
\( A=\{1,2,4,5,10,20\}\)
\( B=\{3,6,9,12,15,18\}\)
\( C=\{2,4,6,8,10,12,14,16,18,20\}\)
\( \overline{A}=\{3,6,7,8,9,11,12,13,14,15,16,17,18,19\}\)
これを数字が縦にそろうように書くと見やすいですよ。
\( U=\{1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20\}\)
\( A=\{1,2,\hspace{10pt}4,5,\hspace{35pt}10,\hspace{128pt}20\}\)
\( B=\{\hspace{18pt}3,\hspace{18pt}6,\hspace{18pt}9,\hspace{28pt}12,\hspace{30pt}15,\hspace{26pt}18\hspace{30pt}\}\)
\( C=\{\hspace{8pt}2,\hspace{11pt}4,\hspace{8pt}6,\hspace{11pt}8,\hspace{8pt}10,\hspace{14pt}12,\hspace{16pt}14,\hspace{14pt}16,\hspace{12pt}18,\hspace{17pt}20\}\)
\( \overline{A}=\{\hspace{18pt}3,\hspace{18pt}6,7,\,8,9,\hspace{12pt}11,12,13,\,14,15,16,17,18,19 \hspace{16pt}\}\)
（\(a\)）\( A\subset C\)
\( A\) の要素はすべて \(C\) の要素にあるか？
ありません。（誤）
（\(b\)）\( A\cap B=\phi\)
\( A\) と \( B\) に重なった要素は一つもないか？
ありません。（正）
キ：②
（\(c\)）\( (A\cup C)\cap B=\{6,12,18\}\)
\( A\) と \( C\) の結びと \( B\) の要素との交わりは \( 6,12,18\) だけか？
\( A\cap B=\phi\) だったので \( B\cap C\) となり６の倍数だと分かりますが、
\( A\cup C=\{1,2,4,5,6,8,10,12,14,16,18,20\}\)
\( B=\{3,6,9,12,15,18\}\)
の両方にあるのは、\( \{6,12,18\}\) で（正）。
（\(d\)）\( (\overline{A}\cap C)\cup B=\overline{A}\cap (B\cup C)\)
もう一度要素をならべてみます。
\( A=\{1,2,4,5,10,20\}\)
\( B=\{3,6,9,12,15,18\}\)
\( C=\{2,4,6,8,10,12,14,16,18,20\}\)
\( \overline{A}=\{3,6,7,8,9,11,12,13,14,15,16,17,18,19\}\)
\( (\overline{A}\cap C)=\{6,8,12,14,16,18\}\)
\( B=\{3,6,9,12,15,18\}\)
なので左辺の要素は
\( (\overline{A}\cap C)\cup B=\{3,6,8,9,12,14,15,16,18\}\)
また
\( B=\{3,6,9,12,15,18\}\)
\( C=\{2,4,6,8,10,12,14,16,18,20\}\)
\( B\cup C=\{2,3,4,6,8,9,10,12,14,15,16,18,20\}\)
\( \overline{A}=\{3,6,7,8,9,11,12,13,14,15,16,17,18,19\}\)
なので右辺の要素は
\( \overline{A}\cap (B\cup C)=\{3,6,8,9,12,14,15,16,18\}\)
よって
\( (\overline{A}\cap C)\cup B=\overline{A}\cap (B\cup C)\)
（正）です。
ク：⓪
ベン図で確認するとはやいです。
\( A\cap B\) の部分が違うように見えますが \( A\cap B=\phi\) （空集合）
なので要素としては同じなのです。
（２）
数直線を書けば一目瞭然っていうヤツです。
整数などの要素が書き出せる場合はベン図、実数などの要素が書き出せない場合は数直線です。
絶対値や根号を外して書くと
\( p\hspace{10pt}:x＜ 0\,,\,4＜ x\)
\( q\hspace{10pt}:x＜ 0\)
\( r\hspace{10pt}:4＜ x\)
\( s\hspace{10pt}:x＜ -4\,,\,4＜ x\)
「 \( q\) または \( r\) 」は \( x< 0 , 4< x\) で \(p\) と同じことです。（必要十分）
ケ：②
\( s\hspace{10pt}:x＜ -4\,,\,4＜ x \hspace{10pt} \rightarrow \hspace{10pt}r\hspace{10pt}: 4＜ x\)
はいえませんが、
\( s\hspace{10pt}:x＜ -4\,,\,4＜ x \hspace{10pt} \leftarrow \hspace{10pt}r\hspace{10pt}: 4＜ x\)
はいえます。（必要条件だが十分条件でない。）
コ：⓪
〔３〕おきまりの２次関数
\( a\) は「正の定数」であることは忘れそうなので大きく印をしておくと良いですよ。
\( f(x)=ax^2-2(a+3)x-3a+21\)
これを見たら平方完成するでしょう。
\( f(x)=ax^2-2(a+3)x-3a+21\\ \\
=a\left\{ x^2-\displaystyle \frac{2(a+3)}{a}x \right\}-3a+21\\ \\
=a\left\{ \left(x-\displaystyle \frac{(a+3)}{a}\right)^2-\displaystyle \frac{(a+3)^2}{a^2} \right\}-3a+21\\ \\
=a \left(x-\displaystyle \frac{a+3}{a}\right)^2-\displaystyle \frac{(a+3)^2}{a} -3a+21\\ \\
=a \left(x-\displaystyle \frac{a+3}{a}\right)^2+\displaystyle \frac{-(a+3)^2+a(-3a+21)}{a}\\ \\
=a \left(x-\displaystyle \frac{a+3}{a}\right)^2+\displaystyle \frac{-(a^2+6a+9)-3a^2+21a}{a}\\ \\
=a \left(x-\displaystyle \frac{a+3}{a}\right)^2+\displaystyle \frac{-a^2-6a-9-3a^2+21a}{a}\\ \\
=a \left(x-\displaystyle \frac{a+3}{a}\right)^2+\displaystyle \frac{-4a^2+15a-9}{a}\)
変形をていねいにやりましたが、計算力に応じて合わせてください。
頂点の \( x\) 座標 \( p\) は
\( p=\displaystyle \frac{a+3}{a}=\fbox{1}+\displaystyle \frac{\fbox{3}}{a}\)
サ：１ シ：３
軸は \(\displaystyle x=1+\frac{3}{a}\) で正です。
\( 0≦ x ≦ 4\) での最小値が \( f(4)\) となる、
つまり、\( x=4\) で最小となるということは \( 0≦ x≦ 4\) で減少しているということです。
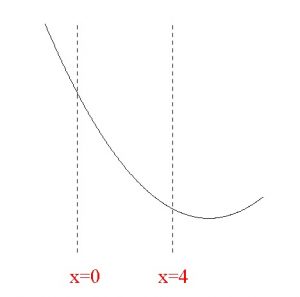
これを満たすには軸が４以上に無ければダメです。
\( 4≦ 1+\displaystyle \frac{3}{a}\\ \\
\Leftrightarrow \hspace{10pt} 4a≦ a+3\\ \\
\Leftrightarrow \hspace{10pt} 3a≦ 3\\ \\
\Leftrightarrow \hspace{10pt} a≦ 1\)
ここで \(0< a\) なので範囲に加えて
\( 0＜ a≦ \fbox{1}\)
ス：１
次に
\( p\) ってなんだっけ？
最初に求めた頂点の \( X\) 座標です。
頂点が最小値になるのは定義域に頂点があることなので、
\( 0≦ x ≦ 4\) に頂点があれば良いということです。
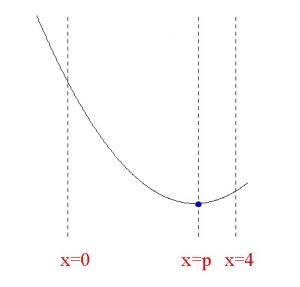
\( 0≦ 1+\displaystyle \frac{3}{a}≦ 4\\ \\
\Leftrightarrow \hspace{10pt} 0＜ a+3≦ 4a\)
\( 0<a\) なので \( a+3≦ 4a\) を考えるだけでいい。
\( 3≦ 3a \Leftrightarrow \fbox{1}≦ a\)
セ：１
でました。「したがって」
何にしたがうか？です。
最小値は２つ可能性があることを誘導してくれています。
\( 0≦x ≦ 4\) に頂点が「ある」場合と、「無い」場合の２つです。
ⅰ） \( 0< a< 1\) のとき最小値は \( f(4)\)
ⅱ） \( 1≦ a\) のとき 最小値は \( f(p)\)
これらの最小値が「１」となる場合を調べます。
後は機械的に解いて行きましょう。
ⅰ） \( 0< a≦ 1\) の場合
\( f(4)=a(4)^2-2(a+3)(4)-3a+21\\ \\
=16a-8(a+3)-3a+21\\ \\
=16a-8a-24-3a+21\\ \\
=5a-3=1\)
より
\( a=\displaystyle \frac{\fbox{4}}{\fbox{5}}\)
これは \( 0< a≦ 1\) に適しています。
ⅱ） \( 1≦ a\) の場合
\( f(p)=f(1+\displaystyle \frac{3}{a})=\displaystyle \frac{-4a^2+15a-9}{a}\)
頂点の \( y\) 座標で、これが「１」となる。
平方完成した形を見なおしましょう。
\( \displaystyle \frac{-4a^2+15a-9}{a}=1\\ \\
\Leftrightarrow \hspace{10pt} -4a^2+15a-9=a\\ \\
\Leftrightarrow \hspace{10pt} -4a^2+14a-9=0\\ \\
\Leftrightarrow \hspace{10pt} 4a^2-14a+9=0\\ \\
\Leftrightarrow \hspace{10pt} a=\displaystyle \frac{7\pm \sqrt{49-36}}{4}\\ \\
\Leftrightarrow \hspace{10pt} a=\displaystyle \frac{7\pm \sqrt{13}}{4}\)
これは \( 1≦ a\) を見ているので
\( a=\displaystyle \frac{\fbox{7}+\sqrt{\fbox{13}}}{\fbox{4}}\)
ⅰ）とⅱ）は「または」で結びます。
ソ，タ：４，５ チ，ツテ，ト：７，１３，４
\( 3=\sqrt{9}＜ \sqrt{13}＜ \sqrt{16}=4\)
なので \(\displaystyle \frac{7-\sqrt{13}}{4}< 1\) です。
続いて第２問（三角比とデータの分析）
⇒ センター試験過去問2018年度数学ⅠＡ第2問（三角比とデータの分析）の解説
に進んで下さい。
過去問のまとめで数年分みて第\(\,1\,\)問の傾向を知ってから対策しても良いです。