2018年、平成30年度のセンター試験過去問、数学ⅠA第3問(確率)の解答と解説になります。
場合の数と確率という範囲ですが、今年は確率のみに見えます。
ただ、場合の数で行う基本的なことは含まれているので、確率だけだったというのは限定しすぎです。
2018年(平成30年)度センター試験問数学ⅠAの問題
センター試験の問題は大学入試センターにもありますので確認してください。
ここでの解説はちょっと変わっているかもしれませんが、得点を優先しているのでご了承下さい。
第3問(選択)確率の解説
第3問~第5問までは2問選択なのでどの2つを選ぶかで少し得点が変わってくるでしょうか。
確率です。
同時に投げても一つずつ2回投げても同じ
2個のサイコロなので表が使えますね。
(1)各事象を見ておきましょう。
A を「大きいさいころについて、4の目が出る」という事象
サイコロの出目は1から6まであるので、4がでる確率は、
\( P(A)=\displaystyle \frac{\fbox{1}}{\fbox{6}}\)
B を「2個のさいころの出た目の和が7である」という事象
2個のさいころの出た目の「和」は
表にすると
| 小\大 | 1 | 2 | 3 | 4 | 5 | 6 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
2個のさいころの和は36通りの出方がありますが、
そのうち「和が7」になるのは赤字の6通り、
よって、
\( P(B)=\displaystyle \frac{6}{36}=\displaystyle \frac{\fbox{1}}{\fbox{6}}\)
B のときと同様に表にすると、
(実際には同じ表で印をかえて見分ければ良いですよ。)
| 小\大 | 1 | 2 | 3 | 4 | 5 | 6 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
「和が9」になるのは青字の4つなので
\( P(C)=\displaystyle \frac{4}{36}=\displaystyle \frac{\fbox{1}}{\fbox{9}}\)
ア:1 イ:6 ウ:1 エ:6 オ:1 カ:9
条件付き確率は公式が無くても出せる
(2)
事象 C が起こったときの事象 A が起こる条件付き確率は
表を書き出しているので公式は使う必要はありません。
| 小\大 | 1 | 2 | 3 | 4 | 5 | 6 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
C が起こるのは和が9の(4通り)、
「そのうち」大きいさいころが4というのは(1通り)です。
よって、
\( P_C(A)=\displaystyle \frac{\fbox{1}}{\fbox{4}}\)
一応公式で解くとどうなるかは見ておきましょう。
公式で表すと
\( P_C(A)=\displaystyle \frac{P(A\cap C)}{P(C)}\)
です。
\( A\cap C\) は大きいさいころが4で、かつ、和が9という事象です。
つまり、大:4 小:5 のときだけ。
これは一通りしかありません。
表の上の数字が大きいさいころの出目だとすると、
4の列を縦に見て合計が9になるのは横の小さいさいころが5のときだけ。
\( P(A\cap C)=\displaystyle \frac{1}{36}\)
よって
\( P_C(A)=\displaystyle \frac{P(A\cap C)}{P(C)}\\ \\
=\displaystyle \frac{\displaystyle \frac{1}{36}}{\displaystyle \frac{1}{9}}=\displaystyle \frac{1}{36}\div \displaystyle \frac{1}{9}=\displaystyle \frac{1}{36}\times \displaystyle \frac{9}{1}=\displaystyle \frac{\fbox{1}}{\fbox{4}}\)
キ:1 ク:4
事象 A が起こったときの事象Cが起こる条件付き確率
これも表を書き出しているので公式は必要ありません。
| 小\大 | 1 | 2 | 3 | 4 | 5 | 6 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
A が起こるだけなら、
和が何でも良いので小さいさいころの目の出方の(6通り)あって、
「そのうち」和が9になるのは小さいさいころが5の(1通り)なので、
(表で見ると4列目の六通りのうち、5行目が「和が9」)
\( P_A(C)=\displaystyle \frac{\fbox{1}}{\fbox{6}}\)
公式で解いてみると
\( P_A(C)=\displaystyle \frac{P(A\cap C)}{P(A)}\\ \\
=\displaystyle \frac{\displaystyle \frac{1}{36}}{\displaystyle \frac{1}{6}}=\displaystyle \frac{1}{36}\div \displaystyle \frac{1}{6}=\displaystyle \frac{1}{36}\times \displaystyle \frac{6}{1}=\displaystyle \frac{\fbox{1}}{\fbox{6}}\)
ケ:1 コ:6
条件付き確率はベン図で解いても公式は必要無い
条件付き確率はベン図で解くのも簡単で良いですよ。
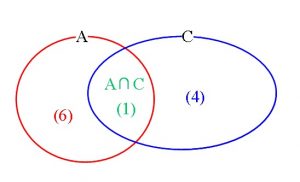
交わり部分を条件のつく方で割れば求まります。
(3)
\( P(A\cap B)\hspace{5pt} \fbox{サ} \hspace{5pt}P(A)P(B)\)
\( P(A\cap C)\hspace{5pt} \fbox{シ} \hspace{5pt}P(A)P(C)\)
確率の大小関係を表せといっています。
これはそれぞれを求めて比較します。
この「メンドクサイ」と思われがちな計算は、
省いてはいけません。
これは簡単に公式だけでは求まらない、
場合をすべて考えて、という問題の意図です。
この大切な「場合を調べる」作業は共通テストになっても変わらないでしょう。
確率、場合の数の基本ですからね。
| 小\大 | 1 | 2 | 3 | 4 | 5 | 6 |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
\( A\cap B\) は大きいさいころの出目が4で、和が7という事象なので、
「大が4、小が3」の一通りだけです。
\( P(A\cap B)=\displaystyle \frac{1}{36}\)
積事象として計算すると
\( P(A\cap B)=\displaystyle \frac{1}{6}\times \displaystyle \frac{1}{6}=\displaystyle \frac{1}{36}\)
\( P(A)\,,\,P(B)\) はそれぞれ求めてあるので、
\( P(A)P(B)=\displaystyle \frac{1}{6}\times \displaystyle \frac{1}{6}=\displaystyle \frac{1}{36}\)
よって
\( P(A\cap B)\hspace{5pt} \fbox{=} \hspace{5pt}P(A)P(B)\)
\( A\cap C\) は大きいさいころの出目が4で、和が9という事象なので、
これも「大が4、小が5」の一通りだけです。
\( P(A\cap C)=\displaystyle \frac{1}{36}\)
また
\( P(A)P(C)=\displaystyle \frac{1}{6}\times \displaystyle \frac{1}{9}=\displaystyle \frac{1}{54}\)
よって
\( P(A\cap C)\hspace{5pt} \fbox{>}\hspace{5pt}P(A)P(C)\)
サ:① シ:②
(4)
大小2個のさいころを同時に投げる試行を2回繰り返す。
1回目に事象 \( A\cap B\) が起こり,
2回目に事象 \( \bar{A}\cap C\) が起こる確率は
1回目の \( A\cap B\) の確率は
\( P(A\cap B)=\displaystyle \frac{1}{36}\)
でした。
2回目に \( \bar{A}\cap C\) が起こる確率は
「大きいさいころが4ではなく、和が9」
になる確率ですが、
大きいさいころが1のときと2のときは和が9にはなりません。
(大,小)=(3,6),(5,4),(6,3)
の三通りしかないので
\( P(\bar{A}\cap C)=\displaystyle \frac{3}{36}=\displaystyle \frac{1}{12}\)
よって、1回目 \( A\cap B\) , 2回目 \( \bar{A}\cap C\) となる確率は
\( \displaystyle \frac{1}{36}\times \displaystyle \frac{1}{12}=\displaystyle \frac{\fbox{1}}{\fbox{432}}\)
ス:1 セソタ:432
続いて
三つの事象 A , B , C がいずれもちょうど1回ずつ起こる確率は
2回の試行で事象 A , B , C が1回ずつ起こるということは、
\( A\,,\,\bar{A}\,,\,B\,,\,C\)
が1回ずつ起こるということです。
ただ、\( A\,,\,\bar{A}\) と \( B\,,\,C\) は同時には起こらないので、
(1回目)→(2回目)が
\( A\cap B \rightarrow \bar{A}\cap C ・・・①\)
\( A\cap C \rightarrow \bar{A}\cap B ・・・②\)
\( \bar{A}\cap B \rightarrow A\cap C ・・・③\)
\( \bar{A}\cap C \rightarrow A\cap B ・・・④\)
となる4つの場合があり、
求める確率は①~④の確率の和になります。
①と④は同じ確率で
\( P(A\cap B)\cdot P(\bar{A}\cap C)=\displaystyle \frac{1}{36}\times \displaystyle \frac{1}{12}\)
\( P(\bar{A}\cap C)\cdot P(A\cap B)=\displaystyle \frac{1}{12}\times \displaystyle \frac{1}{36}\)
②と③は同じ確率で、
\( P(\bar{A}\cap B)\)
は「大きいさいころので目が4ではなく、和が7」という事象の確率なので、
(大,小)=(1,6),(2,5),(3,4),(5,2),(6,1)
の五通りがあることを考えて
\( P(\bar{A}\cap B)=\displaystyle \frac{5}{36}\)
このことから
\( P(A\cap C)\cdot P(\bar{A}\cap B)=\displaystyle \frac{1}{36}\times \displaystyle \frac{5}{36}\)
\( P(\bar{A}\cap B)\cdot P(A\cap C)=\displaystyle \frac{5}{36}\times \displaystyle \frac{1}{36}\)
以上のことから求める確率は
\( \displaystyle \frac{1}{36}\times \displaystyle \frac{1}{12}\times 2+\displaystyle \frac{1}{36}\times \displaystyle \frac{5}{36}\times 2\\ \\
=\displaystyle \frac{1}{36}\times \displaystyle \frac{3}{36}\times 2+\displaystyle \frac{1}{36}\times \displaystyle \frac{5}{36}\times 2\\ \\
=\displaystyle \frac{6+10}{36\times 36}=\displaystyle \frac{16}{36\times 36}=\displaystyle \frac{\fbox{1}}{\fbox{81}}\)
チ:1 ツテ:81
この問題は場合の数ではないですが、
「場合はすべて書き出す」というのは基本にしたいですね。
続いて数学ⅠA第4問です。
⇒ センター試験過去問2018年度の数学ⅠA第4問(整数)の解答と解説
別の問題の解説は
センター試験過去問解説まとめです。