2018年、平成30年度のセンター試験（過去問）の数学ⅠＡ第5問の解答と解説です。
選択問題としての幾何分野となります。
直角三角形から方べきの定理、メネラウスの定理などを使う基本的な問題といえるでしょう。
大小関係を選択肢から選ぶので意味が取れるかどうかがポイントです。
問題は大学入試センターにもあります。
申し訳ありませんが問題をお持ちで無い場合はそちらのページからご確認下さい。
第５問（選択）幾何
先ずやらなければならないのは、
「図を書く」
ことです。
∠Aの二等分線と辺BCとの交点をDとすると，
全体的な図が見えない段階では仮の図を小さく書いて、最後まで目を通せたときに本格的に見やすくすれば良いですよ。
ここまでを図にすると、
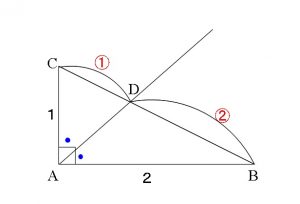
直角三角形の斜辺なので
\(\begin{eqnarray}
\mathrm{BC^2}&=&\mathrm{AB^2+AC^2}\\
&=&2^2+1^2\,=\,5
\end{eqnarray}\)
\( ∴ \hspace{5pt} \mathrm{BD}=\sqrt{5}\)
\(\,\mathrm{D}\,\)は辺\(\,\mathrm{BC}\,\)を\(\,2:1\,\)に内分する点なので、
\(\begin{eqnarray} \displaystyle
\mathrm{BD}&=&\frac{2}{3}\mathrm{BC}\\
&=&\frac{\fbox{2}\sqrt{\fbox{5}}}{\fbox{3}}
\end{eqnarray}\)
次に、
これは図を正確には書きにくいですが雰囲気で大丈夫です。
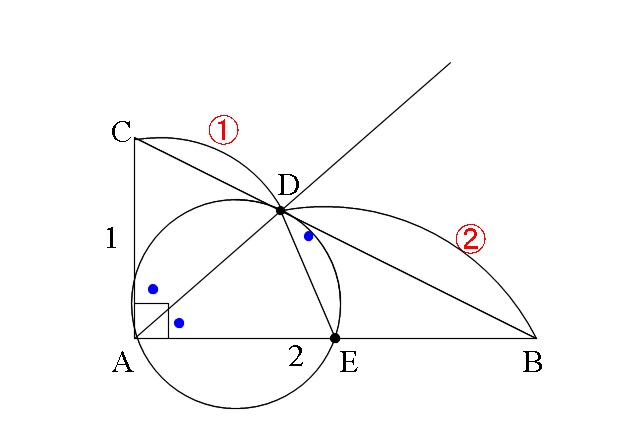
方べきの定理と接弦定理
円と接線と三角形があるので「方べきの定理」ですが、
覚えていなくても「接弦定理」を知っていれば相似です。
\(\,\mathrm{△ABD}\,\)と\(\,\mathrm{△DBE}\,\)において
\( \angle{\mathrm{ABD}}=\angle{\mathrm{DBE}}\) （共通）
また接弦定理より
\( \angle{\mathrm{BAD}}=\angle{\mathrm{BDE}}\)
なので相似 \(\,\mathrm{△ABD}\,\) ∽ \(\,\mathrm{△DBE}\,\) は言えます。
よってそれぞれの辺の比は等しく
\( \mathrm{AB:DB=BD:BE} \\ \\\
\Leftrightarrow \hspace{5pt} \mathrm{AB}\cdot \mathrm{BE}=\mathrm{BD^2}=\left(\displaystyle \frac{2\sqrt{5}}{3}\right)^2=\displaystyle \frac{\fbox{20}}{\fbox{9}}\)
方べきの定理は
\( \mathrm{AB}\cdot \mathrm{BE}=\mathrm{BD^2}\)
です。
辺ABの長さは \( \mathrm{AB}=2\) と分かっているので、
\(\displaystyle \color{red}{\mathrm{AB}}\cdot \mathrm{BE}=\color{red}{2}\mathrm{BE}=\frac{20}{9}\\ \\
\Leftrightarrow \displaystyle \mathrm{BE}=\frac{\fbox{10}}{\fbox{9}}\)
エオ：２０ カ：９ キク：１０ ケ：９
直線ACと直線DEの交点は辺ACの端点の \( \fbox{サ} \) の側にある。
\(\displaystyle \frac{\mathrm{BE}}{\mathrm{BD}} \fbox{コ} \frac{\mathrm{AB}}{\mathrm{BC}}\)
から何故？と思うのではないでしょうか。
これは、
\( \displaystyle \frac{\mathrm{BE}}{\mathrm{BD}}=\displaystyle \frac{\mathrm{AB}}{\mathrm{BC}}\)
のとき辺\(\,\mathrm{AC}\,\)と辺\(\,\mathrm{DE}\,\)が平行になるからです。
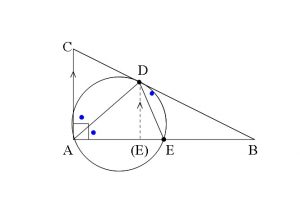
ちょっと意味がとりにくいと思うので先ずは計算して大小関係を出しておきましょう。
\(\begin{eqnarray} \displaystyle
\frac{\mathrm{BE}}{\mathrm{BD}}&=&\displaystyle \frac{\displaystyle \frac{10}{9}}{\displaystyle \frac{2\sqrt{5}}{3}}\\
&=& \frac{10}{9}\div \displaystyle \frac{2\sqrt{5}}{3}\\
&=&\displaystyle \frac{10}{9} \times \displaystyle \frac{3}{2\sqrt{5}}\\
&=& \frac{5}{3\sqrt{5}}
\end{eqnarray}\)
三平方の定理から \( \mathrm{BC}=\sqrt{5}\)だったから
\( \displaystyle \frac{\mathrm{AB}}{\mathrm{BC}}=\displaystyle \frac{2}{\sqrt{5}}=\displaystyle \frac{6}{3\sqrt{5}}\)
よって
\( \displaystyle \frac{\mathrm{BE}}{\mathrm{BD}}\hspace{5pt} \fbox{＜} \hspace{5pt}\displaystyle \frac{\mathrm{AB}}{\mathrm{BC}}\)
これは点\(\,\mathrm{E}\,\)は点\(\,\mathrm{(E)}\,\)より\(\,\mathrm{B}\,\)側にあることを意味しているので、
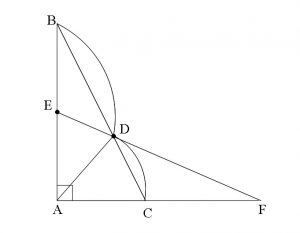
（図を回転してあるので注意してください。）
直線\(\,\mathrm{AC}\,\)と直線\(\,\mathrm{DE}\,\)の交点は辺\(\,\mathrm{AC}\,\)の端点 \(\fbox{C}\) の側の延長上にあります。
コ：⓪ サ：④
いざとなれば、おおよその図から点\(\,\mathrm{F}\,\)は\(\,\mathrm{C}\,\)側と決めつけて、、、ってダメですよね？
メネラウスの定理
図の形から「メネラウスの定理」だと分かるので、図に線分比を書き込んでいきましょう。
角の二等分線だから
\( ＡＣ:ＡＢ=ＣＤ:ＢＤ=1:2\)
\(\,\mathrm{BE}\,\)は求めていて\(\,\mathrm{AB=2}\,\)なので
\(\begin{eqnarray}\displaystyle
\mathrm{AE:EB}&=&\left(2-\frac{10}{9}\right):\frac{10}{9}\\
&=&\frac{8}{9}:\frac{10}{9}\\
&=&4:5
\end{eqnarray}\)
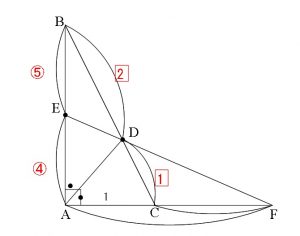
\( \displaystyle \mathrm{\frac{CF}{FA}}\times \displaystyle \mathrm{\frac{AE}{EB}}\times \displaystyle \mathrm{\frac{BD}{DC}}=1\\ \\
\Leftrightarrow \hspace{5pt} \displaystyle \mathrm{\frac{CF}{FA}}\times \displaystyle \frac{4}{5}\times \displaystyle \frac{2}{1}=1\\ \\
\Leftrightarrow \hspace{5pt} \displaystyle \mathrm{\frac{CF}{FA}}=\displaystyle \frac{\fbox{5}}{\fbox{8}}\)
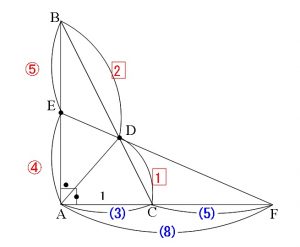
このことから（図で確認して下さい。）
\(\begin{eqnarray} \displaystyle
\mathrm{CF}&=&\frac{5}{3}\cdot \mathrm{AC}\\
&=&\frac{\fbox{5}}{\fbox{3}}
\end{eqnarray}\)
シ：５ ス：８ セ：５ ソ：３
三平方の定理から
\(\begin{eqnarray} \displaystyle
\mathrm{BF^2}&=&\mathrm{AB^2+AF^2}\\
&=&2^2+\left(\frac{8}{3}\right)^2\\
&=&4+\frac{64}{9}\\
&=&\frac{100}{9}
\end{eqnarray}\)
\( ∴ \hspace{5pt} \mathrm{BF}=\displaystyle \frac{10}{3}\)
\(\displaystyle \mathrm{\frac{CF}{AC}}=\mathrm{\frac{BF}{AB}}\) は示さなくて良いようです。
これは何を意味しているかというと、
\(\mathrm{AC:CF\,=\,BA:BF}\)
つまり、\(\,\mathrm{BC}\,\)が \( \angle{\mathrm{ABF}}\) の二等分線になっているといいたいのです。
点\(\,\mathrm{D}\,\)は内角の二等分線の交点になっているので、
\(\,\mathrm{△ABF}\,\)の「内心」です。
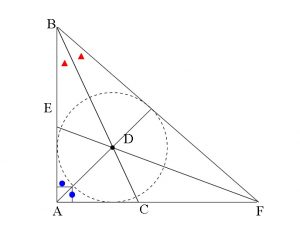
試験場で手書きの内接円がきれいに接することはありません。
多少円を歪めて、接しているように自分で思い込めば良いのですよ。
以上です。
ミスや間違いがあったらごめんなさい。
数学ⅠＡの第１問に戻る場合まとめページからどうぞ。
また
数学\(\,\mathrm{ⅠＡⅡＢ}\,\)の要点はこちらにあります。
ここに書いてあることを外して問題は作れません。