対数の底や真数に未知数がある対数不等式の解き方です。
対数関数のグラフをイメージしながら解けば、指数の方程式や不等式も同じ要領で解くことができます。
方程式といっしょにしても良かったのですが大小関係が出てくるので分けておきました。
問題は簡単なものを取り上げていますので基本の確認としてください。
対数不等式を解くときの方針
指数方程式や不等式、対数方程式でもいっていることですが「底」をそろえることが第1の方針となります。
これは対数不等式でも同じです。
底をそろえる「底の変換」
\(\hspace{10pt}\displaystyle \color{red}{\log_{a}b = \frac{\log_{c}b}{\log_{c}a}}\)
はできるようになっているものとして、
手間を省いたものを例題として選んでいますので、真数の処理に集中してください。
次の不等式を解け。
(1) \( \log_{3}(x-4) + \log_{3}(x-6)< 1\)
(2) \( 2(\log_{5}x)^2-3(\log_{5}x)+1< 0\)
対数不等式も普通の不等式と同じです。
グラフの位置関係から考えれば大丈夫です。
ただ、対数方程式と同様に『真数条件』は真っ先に出しておきましょう。
対数不等式でも真数条件から
(1) \( \log_{3}(x-4) + \log_{3}(x-6)< 1\)
「真数条件」は、
\( x-4\,>\,0\,,\,x-6>\,0\)
より
\(\hspace{10pt}\underline{ x\,>\,6 } ・・・①\)
\(\hspace{10pt} \log_{3}(x-4) + \log_{3}(x-6)< 1\\ \\
\Leftrightarrow \hspace{5pt} \log_{3}(x-4)(x-6)< 1\\ \\
\Leftrightarrow \hspace{5pt} \log_{3}(x-4)(x-6)< \log_{3}3\)
ここで、底が3>1で \(y=\log{3}x\) は増加関数なので、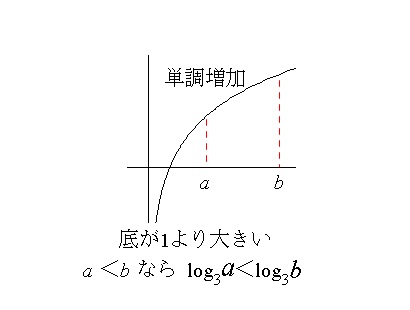
対数の大小は真数の大小に一致します。
よって、
\(\hspace{10pt} (x-4)(x-6)< 3\\ \\
\Leftrightarrow \hspace{5pt} x^2-10x+24< 3\\ \\
\Leftrightarrow \hspace{5pt} x^2-10x+21< 0\\ \\
\Leftrightarrow \hspace{5pt} (x-3)(x-7)< 0\)
これから
\(\hspace{10pt} 3<\,x\,<\,7 ・・・②\)
\(\,①②\,\)より、(真数条件を忘れずに!)
\( \underline{ 6\,<\,x\,<\,7 }\)
(2) \( 2(\log_{5}x)^2-3(\log_{5}x)+1< 0\)
先ず真数条件です。
\(\hspace{10pt} x\,>\,0 ・・・①\)
方程式同様に、\( \log_{5}x\) という共通部分があるのでこれを \( t\) とでも置きましょう。
「置換したら定義域の変換」、
ですがここでは \( x > 0\) において \( t\) は実数全体となります。
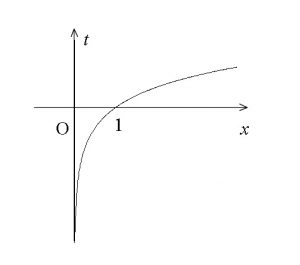
では、不等式を解いてみましょう。
\( \hspace{10pt}2\,(\,\log_{5}x)^2-3(\log_{5}x)+1 \,<\,0\)
において \( \log_{5}x=t\) とおくと、
\(\hspace{10pt} 2t^2-3t+1\,< \,0\\ \\
\Leftrightarrow \hspace{5pt} (2t-1)(t-1)\,< \,0\\ \\
\Leftrightarrow \hspace{5pt} \displaystyle \frac{1}{2}\,< \,t\, < \,1\)
これに \( t=\log_{5}x\) を戻すと、
\(\hspace{10pt} \displaystyle \frac{1}{2}\,< \,t\, < \,1\\ \\
\Leftrightarrow \hspace{5pt} \displaystyle \frac{1}{2}\,< \,\log_{5}x\, < \,1\)
ここで少し迷うかもしれませんが数の大小や不等式では、
「数の世界を統一する」
というのを中学数学でやってますよね?
対数の大小比較のポイント
分数と整数と対数が混じっています。
対数を整数には変えられませんが、分数や整数は対数に変えることができます。
\(\hspace{10pt}\displaystyle \color{red}{\frac{1}{2}}\,<\,\log_{5}x\,<\,\color{red}{1}\\ \\
\displaystyle \Leftrightarrow \log_{5}5^{\color{red}{\frac{1}{2}}} \,<\, \log_{5}x \,<\,\log_{5}5^\color{red}{1}\)
ここでも底が1より大きいので、真数の大小はそのまま一致します。
よって、
\(\hspace{10pt} \log_{5}5^{\frac{1}{2}} \,< \,\log_{5}x \,< \,\log_{5}5^1\\ \\
\Leftrightarrow \hspace{5pt} 5^{\frac{1}{2}}\, < \,x\, < 5^1\\ \\
\Leftrightarrow \hspace{5pt} \underline{\sqrt{5} \,< \,x\, < \,5}\)
真数条件は正の実数全体ですが無条件に確認するようにしましょう。
ところで、
底が1より大きい場合は単調増加するので
(\(\,x\,\)が増えるに従って\( \,y\,\)が減ることなく増え続けるだけ)
対数の大小が、真数の大小に一致するとしました。
しかし、底が1より小さい場合は、単調減少するので
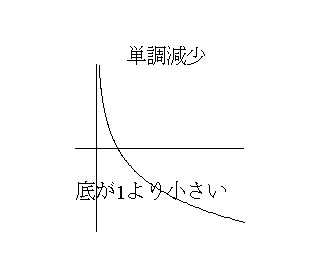
「対数の大小は真数の大小と逆」
になります。
「関数はグラフで考える」ができていれば問題はありません。
しかし、底が1より小さい場合は「底の変換」をして、
「1より大きい底に変えて」
考えれば、すべて単調増加で考えることができますけどね。
いずれにしても 「関数はグラフ!」 です。
最大値、最小値問題も考え方は同じです。
ちょっとしたポイントさえ知っておけば解けるようになります。